MATEMÁTICAS - SECUNDARIA 2
División de números fraccionarios y decimales positivos y negativos
(MAR 15 DICIEMBRE)
ACTIVIDAD:
Resuelve la siguiente situación-problema.
John, un estudiante que reside en Nueva York, Estados Unidos de América, ha llegado a México. Él quiere saber cuáles son las temperaturas más bajas que se han reportado en diferentes lugares de nuestro país, ya que él está acostumbrado a temperaturas de hasta 14 grados Fahrenheit. Al buscar información en los periódicos, encuentra una nota del año 2006 del municipio de La Rosilla, en Durango, que dice que la temperatura mínima reportada de ese lugar fue de -21.5 grados centígrados.
John quiere comparar ambas temperaturas, la de Nueva York de 14 grados Fahrenheit y la de La Rosilla de -21.5 grados centígrados.
¿En qué ciudad es menor la temperatura?
Para poder comparar ambas temperaturas es necesario que éstas se encuentren en las mismas unidades. La fórmula que te puede ayudar para convertir la temperatura de grados centígrados a Fahrenheit es:
La temperatura en grados Fahrenheit es igual a la temperatura en grados centígrados entre 5 novenos más 32.
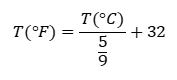
Resuelve el problema y después explica cómo resolviste las operaciones. Comenta a distancia con tus compañeras, compañeros y docentes, qué tipo de números utilizaste.
RESUMEN:
Para iniciar, resuelve el siguiente problema.
Problema, globo aerostático
Un globo aerostático, alcanza una altura de 75 metros en un tiempo de 30 minutos, desde que despegó del suelo.
¿Cuál es la rapidez promedio, en metros por minutos, con la que ha subido el globo?
Resuelve el problema y argumenta cuál es la operación que ayuda a determinar la rapidez promedio. Presta atención en las unidades.
Ahora que ya pensaste cómo resolver el problema, verifica tus resultados.
Recuerda que la rapidez con la que se mueve un móvil es la distancia recorrida entre el tiempo empleado en recorrerla.
Para obtener la rapidez con la que ha subido el globo, puedes dividir la distancia, en este caso, la altura que ha alcanzado el móvil, que es de 75 metros, entre el tiempo de 30 minutos, que fue lo que tardó en llegar a esa altura.
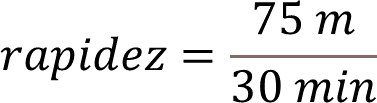
Al simplificar el cociente, obtienes que la rapidez promedio con la que alcanzó esa altura es de, 15 sextos o cinco medios, ya que la tercera parte de 15 es cinco y la tercera parte de 6 es dos, a su vez, al dividir cinco entre dos, es de 2.5 metros por minuto.
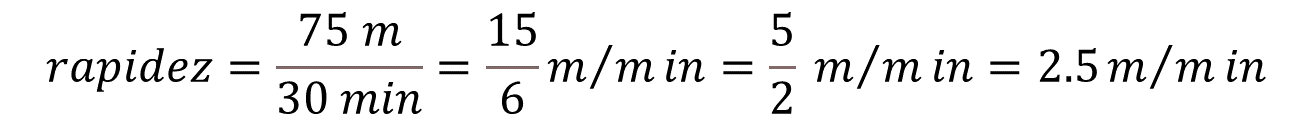
Como puedes observar, al dividir un número positivo entre otro positivo el resultado es positivo. Pero ¿qué significa el número decimal?
Significa que, en promedio, por cada minuto que transcurre, el globo sube una altura de 2.5 metros.
Continúa explorando el tema de esta sesión. Para ello, resuelve el siguiente acertijo.
Acertijo 1:
La tercera parte de un número es, 0.5 negativo.
¿Ya sabes cómo resolverlo?
Primero, plantea una expresión que exprese el acertijo. Recuerda que a la incógnita se le llama “x”, entonces tienes que:
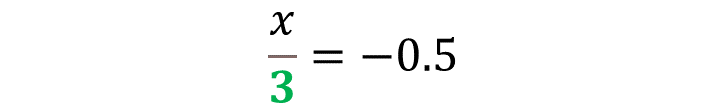
¿Cómo puedes obtener el valor numérico de “x”?
Basta con multiplicar 0.5 negativo por tres. Ya que el inverso de obtener la tercera parte de un número es multiplicarlo por tres.
Ahora realiza la operación:
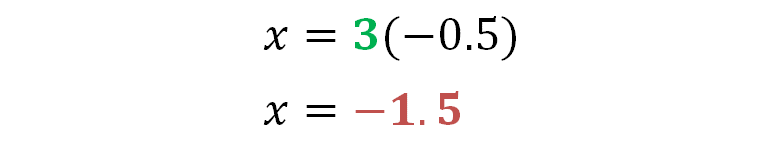
Entonces “x” es igual a 1.5 negativo. Esto quiere decir que, al dividir 1.5 negativo entre tres se obtiene a 0.5 negativo.
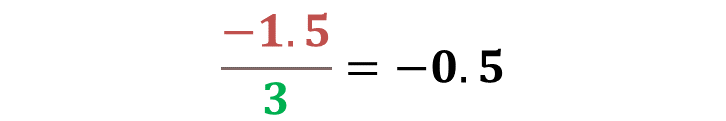
Reflexiona acerca de la división y su resultado. Al dividir un número negativo “-1.5” entre otro positivo “3”, el cociente es negativo, sin importar si los números son decimales, enteros o una combinación de ellos.
Ahora, resuelve el segundo acertijo.
Acertijo 2:
Un número “x” tal que, al dividirlo entre 3 medios negativo sea igual a 2 tercios negativo.
¿Cuál es ese número?
Recuerda que “x” es el número desconocido que debes encontrar. Una forma de comprobar la división es multiplicando el divisor por el cociente y sumarle el residuo para obtener el dividendo. Cuando el residuo es cero, basta con multiplicar el divisor por el cociente.
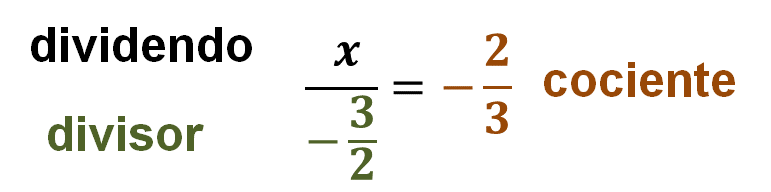
Al aplicar lo anterior en el acertijo, tienes que “x” es igual a 2 tercios negativo por 3 medios negativo. El producto de dos números negativos es positivo, entonces “x” es positivo. Por otro lado, operatoriamente el producto de dos números fraccionarios se obtiene multiplicando los numeradores y los denominadores, respectivamente.
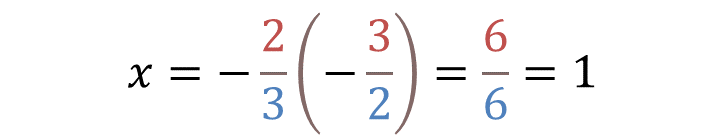
Entonces “x” es igual a un entero. Y como “x” es igual a 1, tienes que uno entre 3 medios negativo es igual a dos tercios negativo.
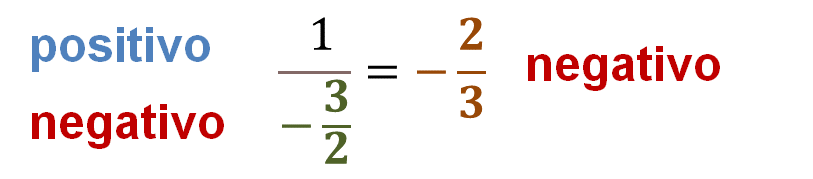
Analizando el tipo de números, se puede concluir que un número positivo entre otro negativo es un número negativo.
Continúa con el tercer acertijo.
Acertijo 3:
Al dividir 35 sextos negativo entre un número, se obtienen 5 medios negativo.
¿De qué número se trata?
Utiliza la estrategia del acertijo anterior. Formula una expresión en la cual, el número desconocido lo representes con la letra “x”, entonces tienes que, al dividir 35 sextos negativo entre “x”, el resultado es igual a 5 medios negativo.
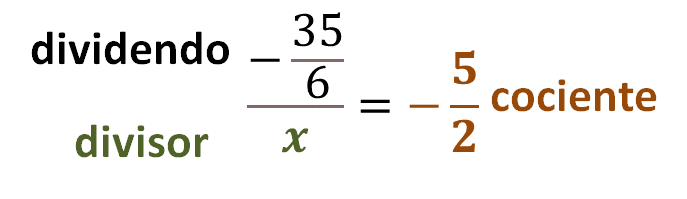
El producto del divisor por el cociente es igual al dividendo; en otras palabras, si multiplicas 5 medios negativo por “x”, debe resultar el dividendo 35 sextos negativo.
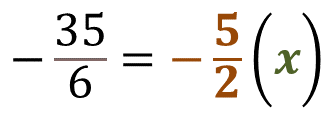
Ahora, busca ese número. Primero identifica el tipo de número que debe ser “x”.
¿“x” es positivo o negativo?, ¿fraccionario o entero?
“x” no puede ser un número negativo, ya que un negativo por otro negativo daría un número positivo, entonces “x” debe ser un número positivo.
También te puedes percatar de que “x” debe ser un número fraccionario, ya que al multiplicar 5 por 7 obtienes 35, de la misma forma, al multiplicar 2 por 3 obtienes 6.
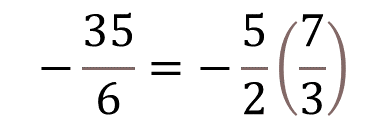
Entonces el valor numérico de “x” es 7 tercios, y es positivo.
Regresando a la expresión original, tienes que, 35 sextos negativo, entre 7 tercios es igual a 5 medios negativo.
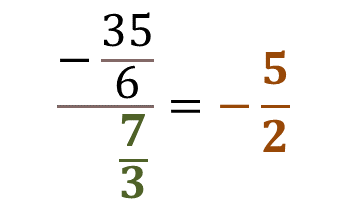
Reflexiona acerca de esta expresión:
Así como 10 entre 2 es igual a 5, también lo es 10 entre 5 igual a 2.

Entonces, análogamente tienes que:
35 sextos negativo entre 7 tercios es igual a 5 medios negativo, o también 35 sextos negativo entre 5 medios negativo es igual a 7 tercios.
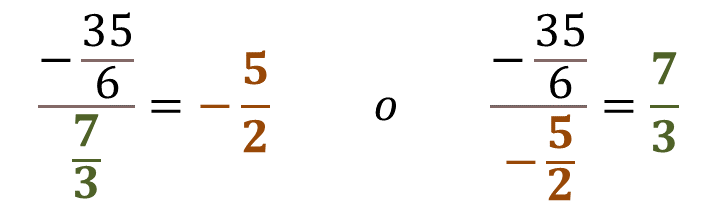
Analiza detalladamente la segunda expresión:
Puedes observar que al dividir un número negativo entre otro negativo obtienes como resultado un número positivo.
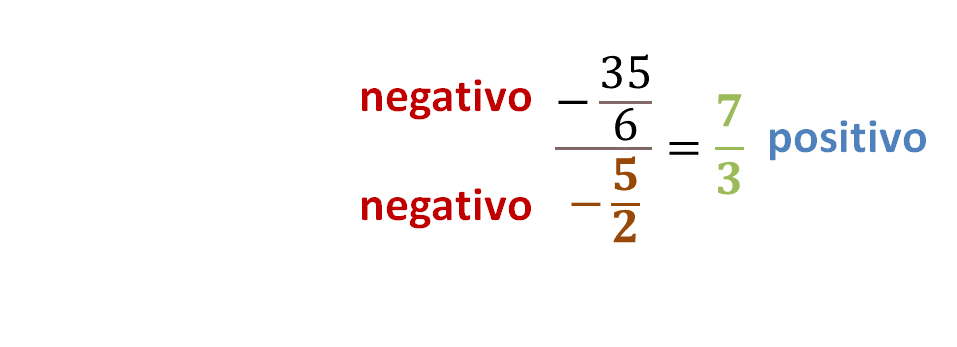
Analiza otro acertijo.
Acertijo 4:
El producto de un quinto negativo por “x” es igual a 3 cuartos negativo. ¿Cuál es ese número?
Formula la expresión matemática que modela el acertijo.
Un quinto negativo por “x” es igual a tres cuartos negativo.
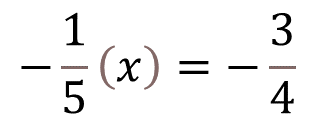
¿Qué tipo de número es “x”?
“x” debe ser un positivo, ya que al multiplicar un número negativo por otro positivo resulta un número negativo.
En este caso, puedes buscar una fracción equivalente a 3 cuartos negativo que tenga como denominador 20 porque el denominador del primer factor es 5 y el del producto es 4. Así que la fracción equivalente a tres cuartos negativo es 15 veinteavos negativo.
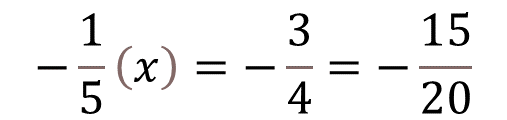
Ahora, verifica si puedes encontrar un número fraccionario tal que, al multiplicarlo por un quinto negativo obtengas 15 veinteavos negativo.
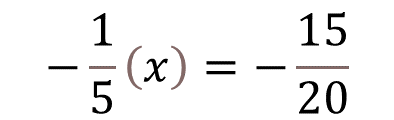
Al dividir 15 entre 1 obtienes 15 en el numerador, y al dividir 20 entre 5 obtienes 4 en el denominador.
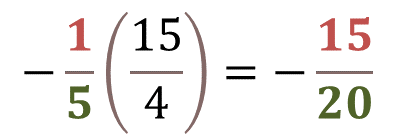
Por lo tanto, “x” es igual a 15 cuartos.
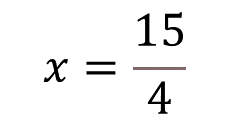
Ahora, verifícalo sustituyendo a “x” por 15 cuartos en la expresión original. Al resolver la operación, tienes que un número negativo por otro positivo es un negativo, luego se multiplican los numeradores, 1 por 15 igual a 15, que es el numerador; y 5 por 4 igual a 20, que es el denominador del producto.
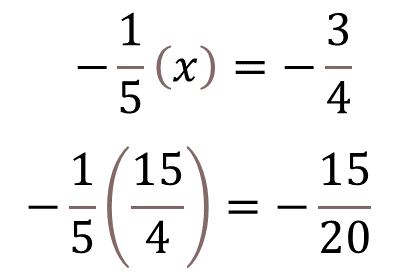
Al simplificar el producto tienes que 15 veinteavos negativo es equivalente a 3 cuartos negativo.
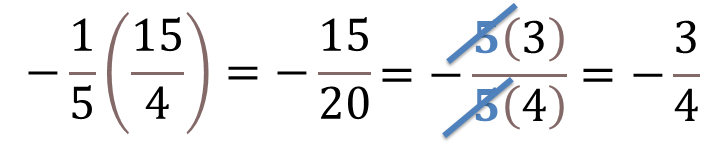
Analiza este producto y exprésalo como una división, tienes dos opciones. La primera de ellas es por medio de la igualdad.
Reflexiona:
¿Cómo puedes obtener el cociente de dos números fraccionarios?
Primero, un número negativo entre otro negativo resulta un número positivo.
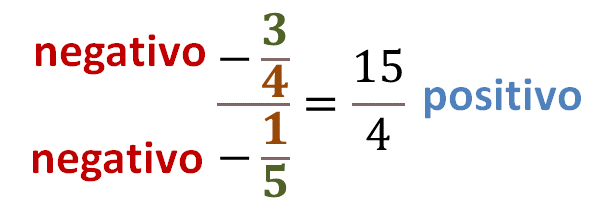
¿Cuáles son los números que se pueden multiplicar para obtener el número 15? Y, ¿cuáles para obtener el 4?
Si se multiplica tres por 5 obtienes a 15, que es el numerador del cociente; y 4 por 1 es el denominador del cociente. Se sabe que el inverso multiplicativo de 1 quinto negativo es menos 5 entre uno. Por lo tanto, puedes convertir una división de fracciones en un producto, utilizando el inverso multiplicativo del divisor.
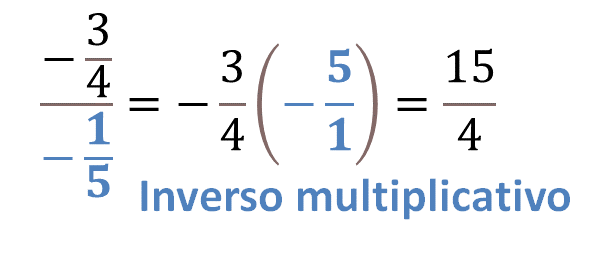
A continuación, realiza lo siguiente.
En tu cuaderno, describe con tus palabras el procedimiento para dividir: dos números fraccionarios positivos; dos números fraccionarios negativos; y dos números fraccionarios, uno positivo y otro negativo; acompañados de un ejemplo creado por ti.
Ahora, analiza el siguiente problema.
Problema, submarino
Un submarino tarda 9 segundos en sumergirse 20 metros. ¿Cuál es la razón de inmersión? Y, ¿cuánto tiempo tardará en alcanzar una posición de -55 metros, considerando el nivel del mar como punto de referencia?
Piensa en una estrategia que te permita resolver lo planteado.
Si el punto de referencia es el nivel del mar y en el problema están indicando que se necesita obtener el tiempo en el cual la posición del submarino es de -55 metros, se puede precisar que cuando el submarino esté sumergido, la posición la establecerás como un número negativo.
Entonces, para obtener la razón de inmersión, debes saber que, cuando el submarino se sumerge, se está desplazando hacia el sentido negativo del sistema de referencia, por ello, la razón se obtiene al dividir -20 metros entre 9 segundos. Como el número negativo “-20” entre otro positivo “9” es un número negativo, entonces tienes que la razón es de -20 novenos de metro sobre segundo.
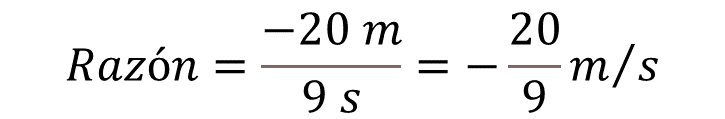
Al realizar la división de 20 entre 9 tienes que, la razón expresada como número decimal es de 2.2 periódico en metros por segundo.
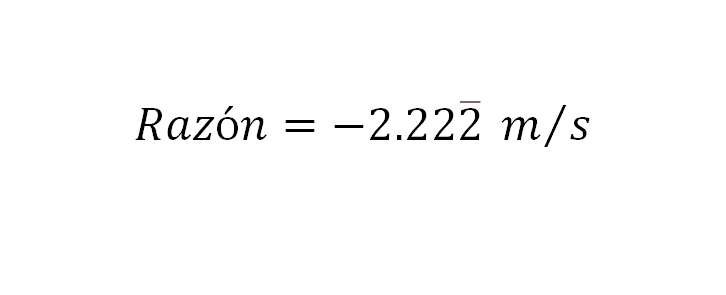
Pero ¿qué quiere decir esta razón?
Quiere decir que cada 9 segundos que pasan, el submarino desciende 20 metros, considerando el nivel del mar como punto de referencia.
Para resolver el segundo cuestionamiento, de ¿cuánto tiempo tardará el submarino en alcanzar una posición de -55 metros? Puedes realizar una estimación.
Manteniendo la razón de inmersión constante, si en 9 segundos el submarino alcanza una posición de -20 metros, en 18 segundos, que es el doble de 9, alcanzará el doble de -20, que es menos 40. De la misma forma, en 27 segundos que es el triple de 9, el submarino alcanzará una posición del triple de menos 20, que es menos 60 metros.
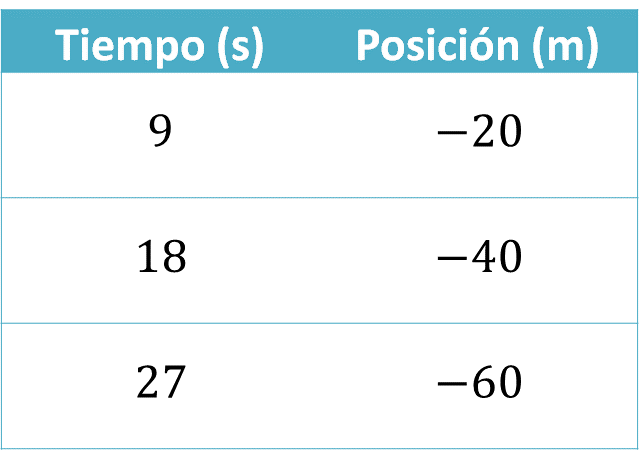
Esto quiere decir que para que el submarino tenga una posición de -55 metros, tardará un poco menos de 27 segundos.
Ahora obtén el tiempo exacto.
¿Cómo puedes calcularlo?
Para obtener el tiempo, basta con dividir la posición entre la razón de inmersión, es decir, -55 metros entre -20 novenos de metro por segundo.
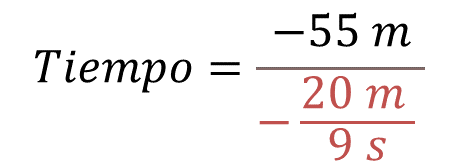
Para dividir números fraccionarios, recuerda que puedes convertir una división de fracciones multiplicando al dividendo por el inverso multiplicativo del divisor, es decir, puedes multiplicar la posición de -55 metros por el inverso multiplicativo de la razón de inmersión que es, -9 segundos entre 20 metros.
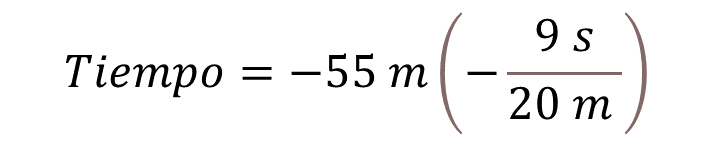
Al resolver la operación tienes que un número negativo por otro negativo es positivo. Ahora multiplica los valores absolutos, 55 por 9 entre 20
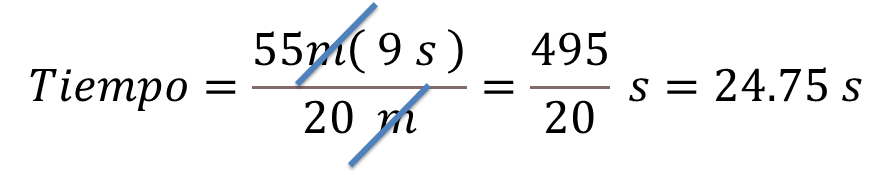
Al realizar el cociente de 495 entre 20, tienes que el tiempo es igual a 24.75 segundos.
¿Hay otra forma de resolver la segunda pregunta? Es decir, de encontrar el tiempo.
Inténtalo con números decimales.
El tiempo lo puedes obtener al dividir la posición entre la razón de desplazamiento, es decir, -55 metros entre -2.2 periódico. Con sus unidades: metros sobre segundo.
Al dividir -55 metros entre -2.2 periódico, en metros por segundo, puedes realizar una aproximación, utilizando cuatro cifras decimales para el número periódico.
Al resolver la operación tienes que un número negativo entre otro negativo es un número positivo y 55 entre 2.2222 es aproximadamente 24.7502 segundos.
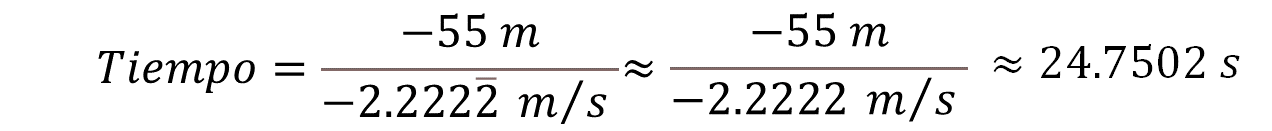
Recuerda que al operar con un número aproximado el resultado es una aproximación, por ello, este tiempo es aproximado.
Has resuelto el problema, pero ¿te has puesto a pensar si un submarino puede desplazarse a esa razón de inmersión?
Analiza a detalle la razón de inmersión.
La razón de inmersión es de -20 metros cada 9 segundos. Para convertir la razón a kilómetros por hora, primero tienes que multiplicar por el factor de conversión 3600 segundos, que equivalen a una hora.
Al multiplicar los factores, obtienes un número negativo, posteriormente al dividir segundos entre segundos, estos se simplifican y queda que 20 por 3600 son 72000 metros entre 9 horas.
Al resolver la división obtienes que -72,000 entre 9 es igual a -8000 metros en una hora, es decir, -8000 metros por hora.
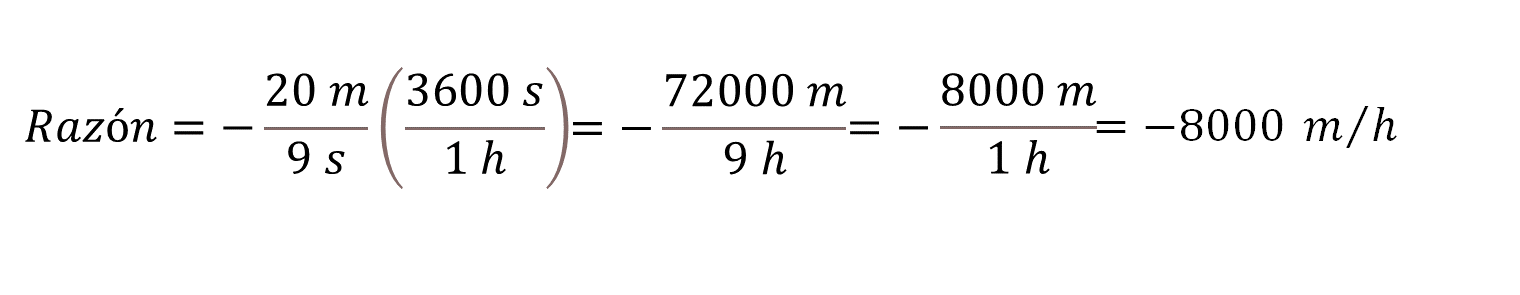
¿Te imaginas sumergirse 8000 metros en una hora?
Ahora conviértelo a kilómetros por hora, multiplicándolo por el factor de conversión, un kilómetro entre mil metros.
Al multiplicar a un número negativo por otro positivo, el producto es negativo, 8000 por uno es 8000, y 1 por 1000 es mil.
Simplifica metros entre metros y obtienes -8000 entre mil kilómetros por cada hora.
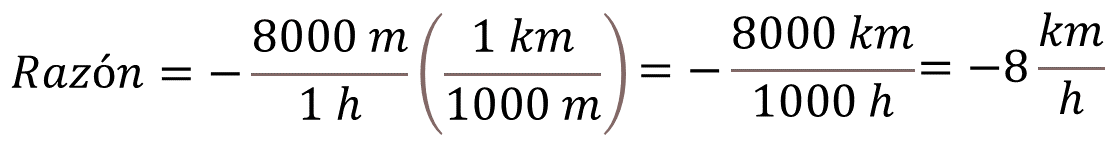
Esto quiere decir que el submarino se sumerge 8 kilómetros por hora.
Si consideras que este submarino se sumerge muy rápido, el submarino nuclear soviético K-162 obtuvo el récord de inmersión en 1970, ya que se desplazaba con una razón de -80 kilómetros por hora.
Resuelve la siguiente situación-problema.
Situación-problema, temperatura
Camila y Jaime, dos estudiantes, investigaron cuál es la temperatura más baja de la Tierra y encontraron muchos datos. Uno de ellos les llamó la atención, encontraron que la temperatura del aire más baja de la Tierra, reportada el 21 de julio de 1983 por la estación meteorológica rusa en la Base Vostok, ubicada en la Antártida Oriental, fue de -128.56° Fahrenheit.
Jaime no reconoce esa escala de temperatura y Camila tampoco sabe a qué temperatura se refiere, porque no saben su equivalencia en grados centígrados, que es la escala que normalmente utilizan.
¿Cuál es la temperatura en grados centígrados?
A continuación, analiza cómo resolvieron esta situación, Camila y Jaime:
Para resolver este problema, Camila decide buscar algunas equivalencias y encuentra que 212 grados Fahrenheit equivalen a 100 grados centígrados, también encuentra que 32 grados Fahrenheit equivalen a cero grados centígrados.
212°F = 100°C y 32°F = 0°C
Por su parte, Jaime investiga una fórmula que le permita convertir la temperatura de grados Fahrenheit a centígrados y encuentra la siguiente fórmula:
La temperatura en grados centígrados es igual a 5 por la temperatura en grados Fahrenheit entre nueve, menos 160 novenos.
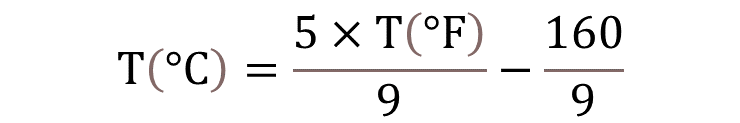
Camila piensa que, de acuerdo con lo que ella investigó, la temperatura en grados centígrados equivalente a menos 128.56 grados Fahrenheit deberá ser negativa.
Jaime para comprobarlo decide utilizar la fórmula que encontró. Al sustituir la temperatura más baja del aire en nuestro planeta, en la fórmula, se tiene que la temperatura en grados centígrados es igual a:
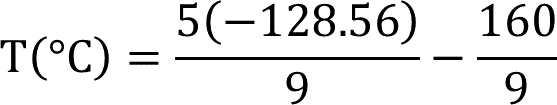
Ahora Camila le recomienda a Jaime que primero realice la multiplicación.
Jaime multiplica 5 por 128.56 negativo, obteniendo 642.8 negativo. Que al dividirlo entre nueve positivo da 71.42222 periódico negativo, y al restarle 160 novenos se obtienen 89.2 negativo.

Cuando Jaime realiza la operación, lo primero que advierte es que 642.8 negativo entre nueve da como resultado un número negativo, posteriormente realiza la división de 642.8 entre 9 igual a menos 71.422 periódico.
Posteriormente, resuelve la resta, a 71.4222 periódico negativo, le resta 160 novenos que equivalen a 17.7 periódico.

Para resolver esta resta, se puede convertir en adición con el simétrico del sustraendo, es decir, 71.4222 periódico negativo más 17.7777 periódico negativo es igual a 89.2 negativo.
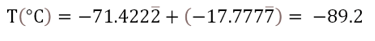
Reflexiona unos segundos acerca del tipo de operaciones y números que se han utilizado para resolver este problema.
Para obtener la temperatura en grados centígrados se han realizado multiplicaciones, divisiones y sumas con números decimales positivos y negativos.
¿Camila estaba en lo correcto?
Camila predijo que la temperatura en grados centígrados equivalente a menos 128.56 grados Fahrenheit debería ser negativa y estaba en lo correcto, ya que la temperatura obtenida es de -89.2 grados centígrados.
-128.56°F = -89.2°C
Con esto has finalizado la sesión, dedicada a la división de números fraccionarios y decimales, positivos y negativos.
Recuerda que este es un material de apoyo, y para complementar lo estudiado, puedes consultar otras fuentes, como tu Libro de Texto de Matemáticas de segundo grado.
Resuelve la siguiente situación-problema.
John, un estudiante que reside en Nueva York, Estados Unidos de América, ha llegado a México. Él quiere saber cuáles son las temperaturas más bajas que se han reportado en diferentes lugares de nuestro país, ya que él está acostumbrado a temperaturas de hasta 14 grados Fahrenheit. Al buscar información en los periódicos, encuentra una nota del año 2006 del municipio de La Rosilla, en Durango, que dice que la temperatura mínima reportada de ese lugar fue de -21.5 grados centígrados.
John quiere comparar ambas temperaturas, la de Nueva York de 14 grados Fahrenheit y la de La Rosilla de -21.5 grados centígrados.
¿En qué ciudad es menor la temperatura?
Para poder comparar ambas temperaturas es necesario que éstas se encuentren en las mismas unidades. La fórmula que te puede ayudar para convertir la temperatura de grados centígrados a Fahrenheit es:
La temperatura en grados Fahrenheit es igual a la temperatura en grados centígrados entre 5 novenos más 32.
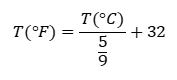
Resuelve el problema y después explica cómo resolviste las operaciones. Comenta a distancia con tus compañeras, compañeros y docentes, qué tipo de números utilizaste.
Para iniciar, resuelve el siguiente problema.
Problema, globo aerostático
Un globo aerostático, alcanza una altura de 75 metros en un tiempo de 30 minutos, desde que despegó del suelo.
¿Cuál es la rapidez promedio, en metros por minutos, con la que ha subido el globo?
Resuelve el problema y argumenta cuál es la operación que ayuda a determinar la rapidez promedio. Presta atención en las unidades.
Ahora que ya pensaste cómo resolver el problema, verifica tus resultados.
Recuerda que la rapidez con la que se mueve un móvil es la distancia recorrida entre el tiempo empleado en recorrerla.
Para obtener la rapidez con la que ha subido el globo, puedes dividir la distancia, en este caso, la altura que ha alcanzado el móvil, que es de 75 metros, entre el tiempo de 30 minutos, que fue lo que tardó en llegar a esa altura.
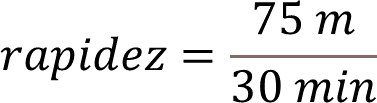
Al simplificar el cociente, obtienes que la rapidez promedio con la que alcanzó esa altura es de, 15 sextos o cinco medios, ya que la tercera parte de 15 es cinco y la tercera parte de 6 es dos, a su vez, al dividir cinco entre dos, es de 2.5 metros por minuto.
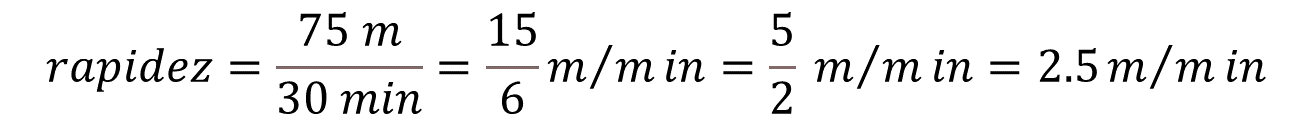
Como puedes observar, al dividir un número positivo entre otro positivo el resultado es positivo. Pero ¿qué significa el número decimal?
Significa que, en promedio, por cada minuto que transcurre, el globo sube una altura de 2.5 metros.
Continúa explorando el tema de esta sesión. Para ello, resuelve el siguiente acertijo.
Acertijo 1:
La tercera parte de un número es, 0.5 negativo.
¿Ya sabes cómo resolverlo?
Primero, plantea una expresión que exprese el acertijo. Recuerda que a la incógnita se le llama “x”, entonces tienes que:
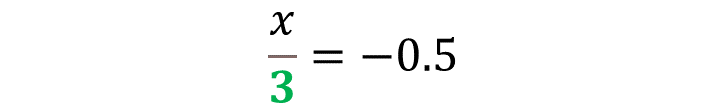
¿Cómo puedes obtener el valor numérico de “x”?
Basta con multiplicar 0.5 negativo por tres. Ya que el inverso de obtener la tercera parte de un número es multiplicarlo por tres.
Ahora realiza la operación:
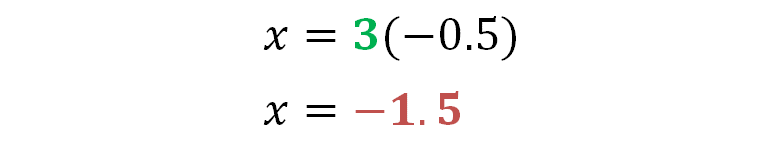
Entonces “x” es igual a 1.5 negativo. Esto quiere decir que, al dividir 1.5 negativo entre tres se obtiene a 0.5 negativo.
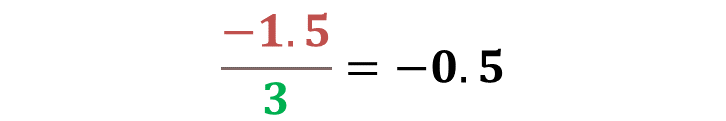
Reflexiona acerca de la división y su resultado. Al dividir un número negativo “-1.5” entre otro positivo “3”, el cociente es negativo, sin importar si los números son decimales, enteros o una combinación de ellos.
Ahora, resuelve el segundo acertijo.
Acertijo 2:
Un número “x” tal que, al dividirlo entre 3 medios negativo sea igual a 2 tercios negativo.
¿Cuál es ese número?
Recuerda que “x” es el número desconocido que debes encontrar. Una forma de comprobar la división es multiplicando el divisor por el cociente y sumarle el residuo para obtener el dividendo. Cuando el residuo es cero, basta con multiplicar el divisor por el cociente.
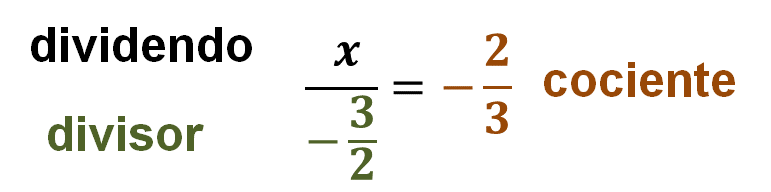
Al aplicar lo anterior en el acertijo, tienes que “x” es igual a 2 tercios negativo por 3 medios negativo. El producto de dos números negativos es positivo, entonces “x” es positivo. Por otro lado, operatoriamente el producto de dos números fraccionarios se obtiene multiplicando los numeradores y los denominadores, respectivamente.
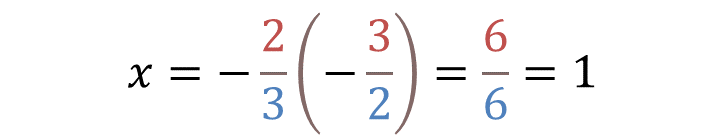
Entonces “x” es igual a un entero. Y como “x” es igual a 1, tienes que uno entre 3 medios negativo es igual a dos tercios negativo.
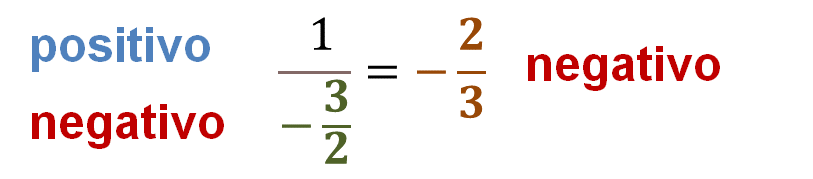
Analizando el tipo de números, se puede concluir que un número positivo entre otro negativo es un número negativo.
Continúa con el tercer acertijo.
Acertijo 3:
Al dividir 35 sextos negativo entre un número, se obtienen 5 medios negativo.
¿De qué número se trata?
Utiliza la estrategia del acertijo anterior. Formula una expresión en la cual, el número desconocido lo representes con la letra “x”, entonces tienes que, al dividir 35 sextos negativo entre “x”, el resultado es igual a 5 medios negativo.
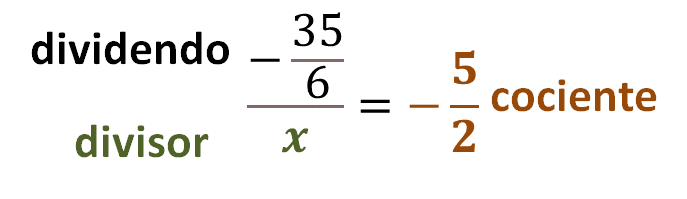
El producto del divisor por el cociente es igual al dividendo; en otras palabras, si multiplicas 5 medios negativo por “x”, debe resultar el dividendo 35 sextos negativo.
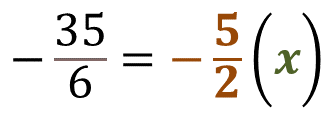
Ahora, busca ese número. Primero identifica el tipo de número que debe ser “x”.
¿“x” es positivo o negativo?, ¿fraccionario o entero?
“x” no puede ser un número negativo, ya que un negativo por otro negativo daría un número positivo, entonces “x” debe ser un número positivo.
También te puedes percatar de que “x” debe ser un número fraccionario, ya que al multiplicar 5 por 7 obtienes 35, de la misma forma, al multiplicar 2 por 3 obtienes 6.
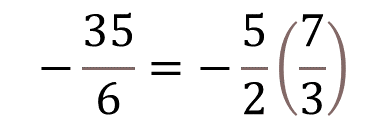
Entonces el valor numérico de “x” es 7 tercios, y es positivo.
Regresando a la expresión original, tienes que, 35 sextos negativo, entre 7 tercios es igual a 5 medios negativo.
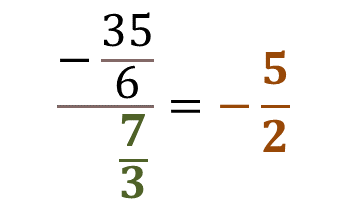
Reflexiona acerca de esta expresión:
Así como 10 entre 2 es igual a 5, también lo es 10 entre 5 igual a 2.

Entonces, análogamente tienes que:
35 sextos negativo entre 7 tercios es igual a 5 medios negativo, o también 35 sextos negativo entre 5 medios negativo es igual a 7 tercios.
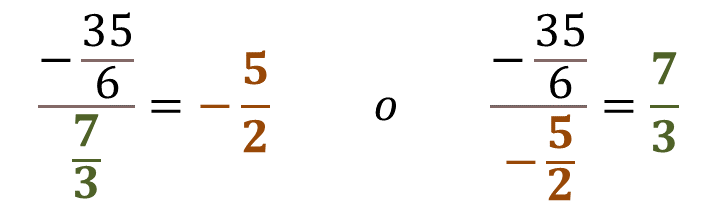
Analiza detalladamente la segunda expresión:
Puedes observar que al dividir un número negativo entre otro negativo obtienes como resultado un número positivo.
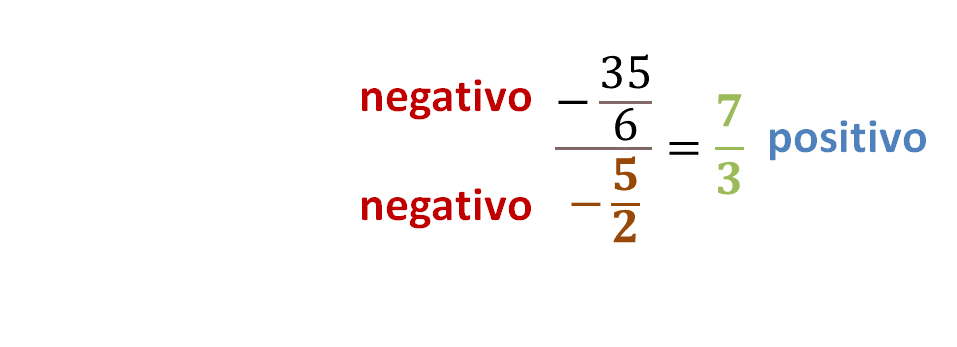
Analiza otro acertijo.
Acertijo 4:
El producto de un quinto negativo por “x” es igual a 3 cuartos negativo. ¿Cuál es ese número?
Formula la expresión matemática que modela el acertijo.
Un quinto negativo por “x” es igual a tres cuartos negativo.
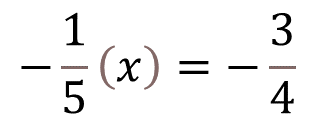
¿Qué tipo de número es “x”?
“x” debe ser un positivo, ya que al multiplicar un número negativo por otro positivo resulta un número negativo.
En este caso, puedes buscar una fracción equivalente a 3 cuartos negativo que tenga como denominador 20 porque el denominador del primer factor es 5 y el del producto es 4. Así que la fracción equivalente a tres cuartos negativo es 15 veinteavos negativo.
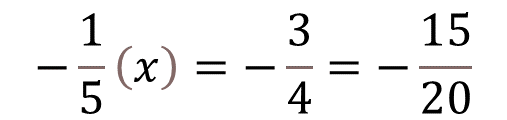
Ahora, verifica si puedes encontrar un número fraccionario tal que, al multiplicarlo por un quinto negativo obtengas 15 veinteavos negativo.
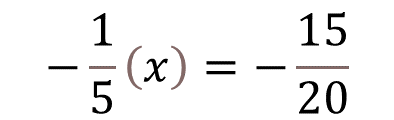
Al dividir 15 entre 1 obtienes 15 en el numerador, y al dividir 20 entre 5 obtienes 4 en el denominador.
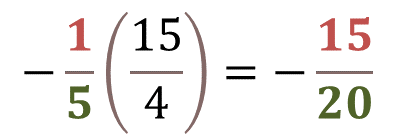
Por lo tanto, “x” es igual a 15 cuartos.
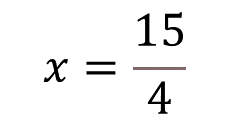
Ahora, verifícalo sustituyendo a “x” por 15 cuartos en la expresión original. Al resolver la operación, tienes que un número negativo por otro positivo es un negativo, luego se multiplican los numeradores, 1 por 15 igual a 15, que es el numerador; y 5 por 4 igual a 20, que es el denominador del producto.
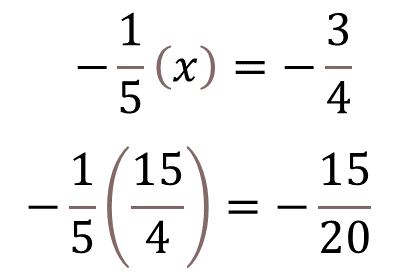
Al simplificar el producto tienes que 15 veinteavos negativo es equivalente a 3 cuartos negativo.
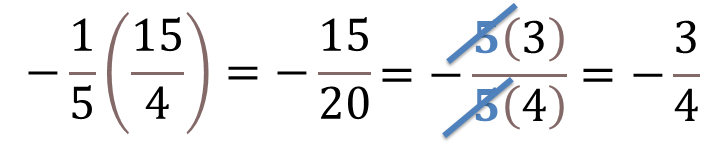
Analiza este producto y exprésalo como una división, tienes dos opciones. La primera de ellas es por medio de la igualdad.
Reflexiona:
¿Cómo puedes obtener el cociente de dos números fraccionarios?
Primero, un número negativo entre otro negativo resulta un número positivo.
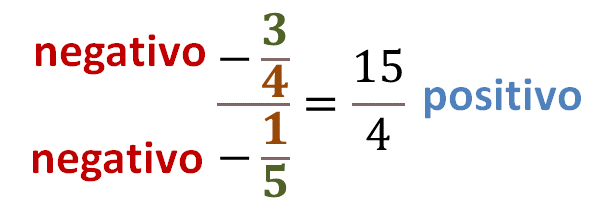
¿Cuáles son los números que se pueden multiplicar para obtener el número 15? Y, ¿cuáles para obtener el 4?
Si se multiplica tres por 5 obtienes a 15, que es el numerador del cociente; y 4 por 1 es el denominador del cociente. Se sabe que el inverso multiplicativo de 1 quinto negativo es menos 5 entre uno. Por lo tanto, puedes convertir una división de fracciones en un producto, utilizando el inverso multiplicativo del divisor.
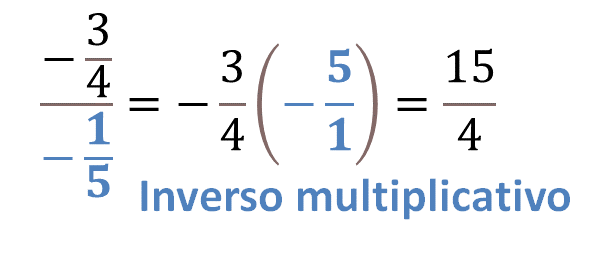
A continuación, realiza lo siguiente.
En tu cuaderno, describe con tus palabras el procedimiento para dividir: dos números fraccionarios positivos; dos números fraccionarios negativos; y dos números fraccionarios, uno positivo y otro negativo; acompañados de un ejemplo creado por ti.
Ahora, analiza el siguiente problema.
Problema, submarino
Un submarino tarda 9 segundos en sumergirse 20 metros. ¿Cuál es la razón de inmersión? Y, ¿cuánto tiempo tardará en alcanzar una posición de -55 metros, considerando el nivel del mar como punto de referencia?
Piensa en una estrategia que te permita resolver lo planteado.
Si el punto de referencia es el nivel del mar y en el problema están indicando que se necesita obtener el tiempo en el cual la posición del submarino es de -55 metros, se puede precisar que cuando el submarino esté sumergido, la posición la establecerás como un número negativo.
Entonces, para obtener la razón de inmersión, debes saber que, cuando el submarino se sumerge, se está desplazando hacia el sentido negativo del sistema de referencia, por ello, la razón se obtiene al dividir -20 metros entre 9 segundos. Como el número negativo “-20” entre otro positivo “9” es un número negativo, entonces tienes que la razón es de -20 novenos de metro sobre segundo.
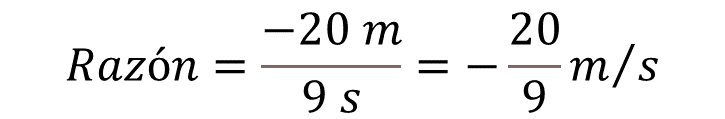
Al realizar la división de 20 entre 9 tienes que, la razón expresada como número decimal es de 2.2 periódico en metros por segundo.
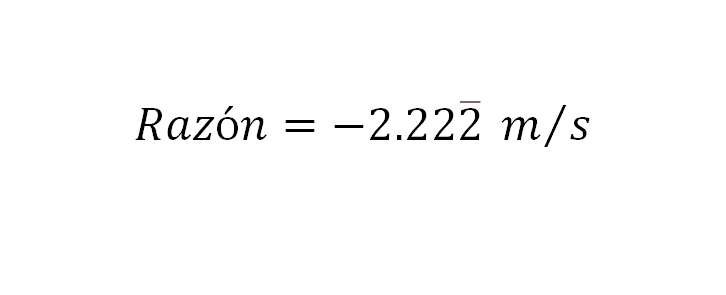
Pero ¿qué quiere decir esta razón?
Quiere decir que cada 9 segundos que pasan, el submarino desciende 20 metros, considerando el nivel del mar como punto de referencia.
Para resolver el segundo cuestionamiento, de ¿cuánto tiempo tardará el submarino en alcanzar una posición de -55 metros? Puedes realizar una estimación.
Manteniendo la razón de inmersión constante, si en 9 segundos el submarino alcanza una posición de -20 metros, en 18 segundos, que es el doble de 9, alcanzará el doble de -20, que es menos 40. De la misma forma, en 27 segundos que es el triple de 9, el submarino alcanzará una posición del triple de menos 20, que es menos 60 metros.

Esto quiere decir que para que el submarino tenga una posición de -55 metros, tardará un poco menos de 27 segundos.
Ahora obtén el tiempo exacto.
¿Cómo puedes calcularlo?
Para obtener el tiempo, basta con dividir la posición entre la razón de inmersión, es decir, -55 metros entre -20 novenos de metro por segundo.
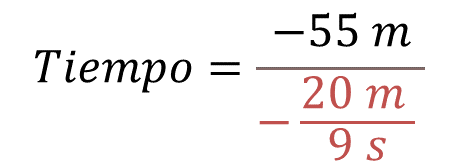
Para dividir números fraccionarios, recuerda que puedes convertir una división de fracciones multiplicando al dividendo por el inverso multiplicativo del divisor, es decir, puedes multiplicar la posición de -55 metros por el inverso multiplicativo de la razón de inmersión que es, -9 segundos entre 20 metros.
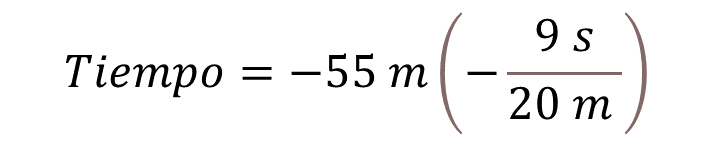
Al resolver la operación tienes que un número negativo por otro negativo es positivo. Ahora multiplica los valores absolutos, 55 por 9 entre 20
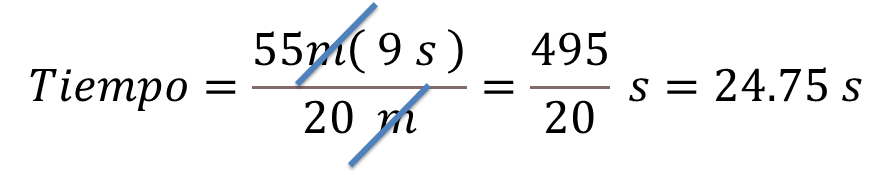
Al realizar el cociente de 495 entre 20, tienes que el tiempo es igual a 24.75 segundos.
¿Hay otra forma de resolver la segunda pregunta? Es decir, de encontrar el tiempo.
Inténtalo con números decimales.
El tiempo lo puedes obtener al dividir la posición entre la razón de desplazamiento, es decir, -55 metros entre -2.2 periódico. Con sus unidades: metros sobre segundo.
Al dividir -55 metros entre -2.2 periódico, en metros por segundo, puedes realizar una aproximación, utilizando cuatro cifras decimales para el número periódico.
Al resolver la operación tienes que un número negativo entre otro negativo es un número positivo y 55 entre 2.2222 es aproximadamente 24.7502 segundos.
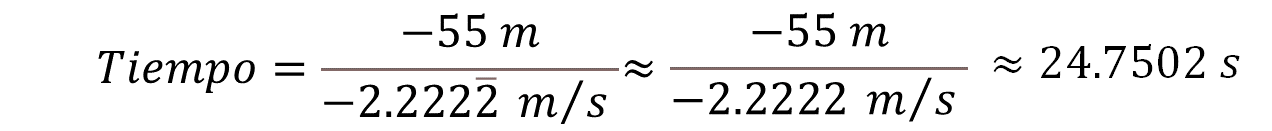
Recuerda que al operar con un número aproximado el resultado es una aproximación, por ello, este tiempo es aproximado.
Has resuelto el problema, pero ¿te has puesto a pensar si un submarino puede desplazarse a esa razón de inmersión?
Analiza a detalle la razón de inmersión.
La razón de inmersión es de -20 metros cada 9 segundos. Para convertir la razón a kilómetros por hora, primero tienes que multiplicar por el factor de conversión 3600 segundos, que equivalen a una hora.
Al multiplicar los factores, obtienes un número negativo, posteriormente al dividir segundos entre segundos, estos se simplifican y queda que 20 por 3600 son 72000 metros entre 9 horas.
Al resolver la división obtienes que -72,000 entre 9 es igual a -8000 metros en una hora, es decir, -8000 metros por hora.
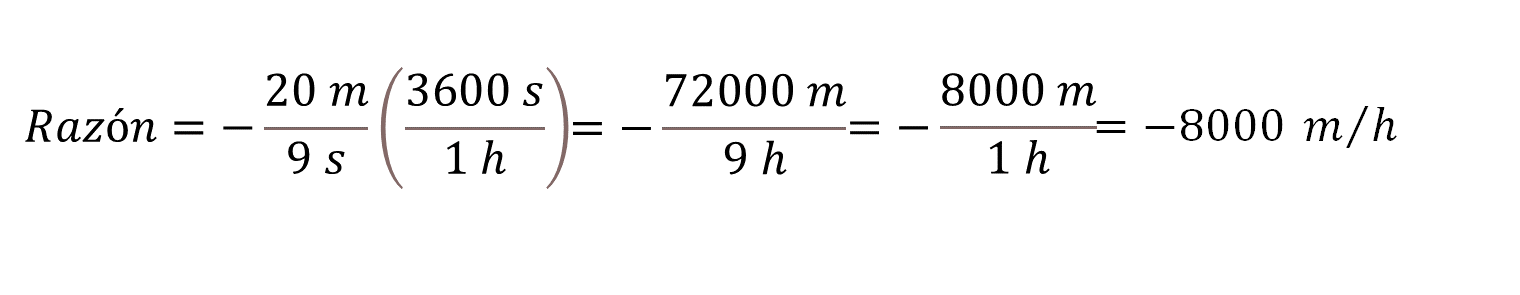
¿Te imaginas sumergirse 8000 metros en una hora?
Ahora conviértelo a kilómetros por hora, multiplicándolo por el factor de conversión, un kilómetro entre mil metros.
Al multiplicar a un número negativo por otro positivo, el producto es negativo, 8000 por uno es 8000, y 1 por 1000 es mil.
Simplifica metros entre metros y obtienes -8000 entre mil kilómetros por cada hora.
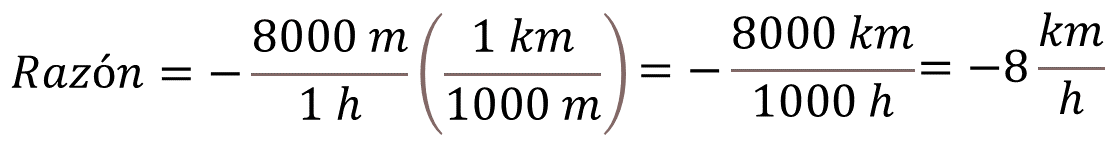
Esto quiere decir que el submarino se sumerge 8 kilómetros por hora.
Si consideras que este submarino se sumerge muy rápido, el submarino nuclear soviético K-162 obtuvo el récord de inmersión en 1970, ya que se desplazaba con una razón de -80 kilómetros por hora.
Resuelve la siguiente situación-problema.
Situación-problema, temperatura
Camila y Jaime, dos estudiantes, investigaron cuál es la temperatura más baja de la Tierra y encontraron muchos datos. Uno de ellos les llamó la atención, encontraron que la temperatura del aire más baja de la Tierra, reportada el 21 de julio de 1983 por la estación meteorológica rusa en la Base Vostok, ubicada en la Antártida Oriental, fue de -128.56° Fahrenheit.
Jaime no reconoce esa escala de temperatura y Camila tampoco sabe a qué temperatura se refiere, porque no saben su equivalencia en grados centígrados, que es la escala que normalmente utilizan.
¿Cuál es la temperatura en grados centígrados?
A continuación, analiza cómo resolvieron esta situación, Camila y Jaime:
Para resolver este problema, Camila decide buscar algunas equivalencias y encuentra que 212 grados Fahrenheit equivalen a 100 grados centígrados, también encuentra que 32 grados Fahrenheit equivalen a cero grados centígrados.
212°F = 100°C y 32°F = 0°C
Por su parte, Jaime investiga una fórmula que le permita convertir la temperatura de grados Fahrenheit a centígrados y encuentra la siguiente fórmula:
La temperatura en grados centígrados es igual a 5 por la temperatura en grados Fahrenheit entre nueve, menos 160 novenos.
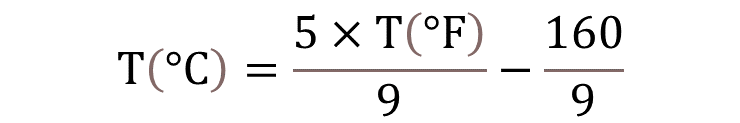
Camila piensa que, de acuerdo con lo que ella investigó, la temperatura en grados centígrados equivalente a menos 128.56 grados Fahrenheit deberá ser negativa.
Jaime para comprobarlo decide utilizar la fórmula que encontró. Al sustituir la temperatura más baja del aire en nuestro planeta, en la fórmula, se tiene que la temperatura en grados centígrados es igual a:
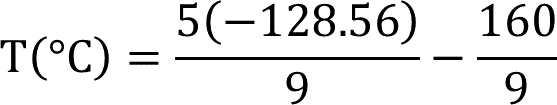
Ahora Camila le recomienda a Jaime que primero realice la multiplicación.
Jaime multiplica 5 por 128.56 negativo, obteniendo 642.8 negativo. Que al dividirlo entre nueve positivo da 71.42222 periódico negativo, y al restarle 160 novenos se obtienen 89.2 negativo.

Cuando Jaime realiza la operación, lo primero que advierte es que 642.8 negativo entre nueve da como resultado un número negativo, posteriormente realiza la división de 642.8 entre 9 igual a menos 71.422 periódico.
Posteriormente, resuelve la resta, a 71.4222 periódico negativo, le resta 160 novenos que equivalen a 17.7 periódico.

Para resolver esta resta, se puede convertir en adición con el simétrico del sustraendo, es decir, 71.4222 periódico negativo más 17.7777 periódico negativo es igual a 89.2 negativo.
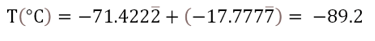
Reflexiona unos segundos acerca del tipo de operaciones y números que se han utilizado para resolver este problema.
Para obtener la temperatura en grados centígrados se han realizado multiplicaciones, divisiones y sumas con números decimales positivos y negativos.
¿Camila estaba en lo correcto?
Camila predijo que la temperatura en grados centígrados equivalente a menos 128.56 grados Fahrenheit debería ser negativa y estaba en lo correcto, ya que la temperatura obtenida es de -89.2 grados centígrados.
-128.56°F = -89.2°C
Con esto has finalizado la sesión, dedicada a la división de números fraccionarios y decimales, positivos y negativos.
Recuerda que este es un material de apoyo, y para complementar lo estudiado, puedes consultar otras fuentes, como tu Libro de Texto de Matemáticas de segundo grado.
No hay comentarios.:
Publicar un comentario