ESPAÑOL - SECUNDARIA 1
Haciendo y deshaciendo se va aprendiendo
(VIERNES 05 FEBRERO)
ACTIVIDAD:
Escribe y responde en tu cuaderno las siguientes preguntas:
- ¿Qué es un pregón, un dicho y un refrán?
- ¿Cómo se distingue uno de otro?
- ¿En qué casos se utiliza cada uno?
- ¿Dónde los han escuchado?
- ¿Quiénes los dicen?
- ¿Ustedes cuáles conocen?
- Y ¿cuál es la diferencia entre lenguaje literal o significado explícito y lenguaje metafórico o significado implícito?
Si desconoces alguna respuesta, puedes revisar los apuntes que realizaste durante la sesión o consultar tus dudas con su maestra o maestro, recuerda que el que busca, encuentra.
Recopila y escribe en tu cuaderno los refranes, dichos o pregones que estuviste leyendo durante el desarrollo de la sesión
RESUMEN:
Sin darte cuenta, de manera continua escuchas o utilizas ciertas frases para comunicarte y relacionarte con otras personas con fines muy variados, como comprar y vender productos, expresar lo que ocurre en el mundo de forma figurada o metafórica o dar un consejo o enseñanza.
Algunas situaciones se repiten con frecuencia. Así las comunidades han aprendido a emplear dichos, refranes y pregones en determinados momentos; así que, para conocer la definición, características y diferencias entre estos conceptos, te invito a echarte un taco de ojo con toda la información que revisarás a continuación.
Los dichos son enunciados que contienen ciertas ocurrencias ingeniosas que se expresan en sentido figurado.
Es decir, con palabras que adquieren un significado distinto al contexto, que no coinciden literalmente con lo que expresan, sino que ilustran una idea o concepto utilizando recursos retóricos, como la metáfora o la ironía.
Por ejemplo, “salvado por la campana” es una frase que se utiliza cuando gracias a que algún suceso se interpone en tus actividades, dejas de realizar una acción que te aburre o desagrada.
Esta es una frase derivada del boxeo y se documenta a principios del siglo XX, y se refiere, por supuesto, al hecho de que la campana marca el final de un round y sirve para tener un minuto de descanso para los boxeadores, lo cual beneficia, particularmente, a aquel que esté siendo más atacado. Así nació el significado de esta frase.
Los dichos también son denominados “expresiones populares” con sonoridad y rima que dan un sentido divertido a nuestras expresiones cotidianas; son una forma de entender la vida a través de analogías sobre diversos temas que se transmiten de generación en generación, y por ser el resultado de años de experiencia son considerados patrimonio de la humanidad.
Otro ejemplo de este tipo de expresiones es: ¡Ya nos cayó el chahuistle! Esta frase tan peculiar es utilizada cuando te sorprenden haciendo algún acto indebido o cuando una persona desagradable se agrega a los planes sin ser requerida.
En México se le nombra chahuistle a una enfermedad producida por un hongo que afecta los cultivos del maíz. Es un término de origen náhuatl “chahuiztli”, que significa “enfermedad de la hoja del maíz”, y que durante cientos de años devastó los cultivos de las comunidades prehispánicas, no hay que olvidar que en la época prehispánica el maíz era parte importante en la economía y tradiciones mesoamericanas, para proteger sus cultivos surgieron rituales, no obstante, el hongo seguía invadiendo la siembra causando desgracias. Así es como surge esta expresión.
Pero ya le echaste mucha crema a los tacos, aprende lo qué son los refranes..
Los refranes son frases que expresan sabiduría popular a través de un consejo o enseñanza en forma metafórica, utilizando palabras distintas a las de uso común para representar la realidad. Su propósito es educativo, hacen referencia a situaciones que cualquier persona puede enfrentar y se transmiten de generación en generación sin importar el origen, las costumbres, la edad o la forma de vida.
Y los antecedentes de los refranes son los proverbios; en la antigüedad, éstos hacían referencia a hechos históricos, costumbres, supersticiones, actividades o personajes célebres de esa época, hoy en día es una tradición oral que se ha mantenido vigente en todo el mundo. Los españoles los consideraban “filosofía popular" por ser enunciados sabios y verdaderos de uso común.
Transmitir los refranes, tradicionalmente de generación en generación, ocasiona que estos puedan sufrir algunas variaciones con el tiempo; por ejemplo, el refrán “perro ladrador poco mordedor” es ahora conocido como “perro que ladra no muerde”. La idea es la misma pero la rima ha desaparecido y la moraleja hace referencia a las personas que gritan mucho o amenazan, pero no cumplen lo dicho con palabras.
Los refranes, al igual que los dichos, no pueden ser tomados de manera literal. Por lo tanto, pueden expresar dos sentidos, uno explícito que resulta fácil de entender por la forma en que está escrito y otro implícito donde debes buscar el significado real, por ejemplo:
El refrán: “Camarón que se duerme se lo lleva la corriente”, en el sentido explícito explica que cuando un camarón está despierto tiene la capacidad de sujetarse bien al fondo del mar, pero cuando éste se descuida o se duerme, la corriente lo arrastrará. En el sentido implícito, el significado de este refrán hace referencia a que si una persona se descuida (se "duerme" en este caso), puede meterse en problemas o salir afectado ("arrastrado por la corriente").
Otros ejemplos de refranes explícitos son:
- El que espera, desespera.
- Hoy por ti, mañana por mí.
- Más vale tarde que nunca.
- Haz el bien sin mirar a quién.
En estos enunciados no necesitas dar una explicación implícita, porque las palabras que utilizas al expresarlos facilitan la comprensión.
Otra característica importante de los refranes es el uso de recursos literarios como la rima, tanto asonante como consonante. La rima es la repetición de sonidos vocálicos y consonánticos, o sólo vocálicos, a partir de la última vocal acentuada en dos o más versos.
Una rima asonante es aquella en la que sólo coinciden los sonidos de las vocales, por ejemplo: “cuanto más se tiene más se quiere”.
La rima consonante es aquella en la que coinciden los sonidos de la última vocal acentuada incluyendo las vocales y las consonantes, por ejemplo: “a lo hecho pecho”.
Los refranes escritos en verso tienen cierto ritmo y resultan más fáciles de recordar; por lo tanto, son aquellos que se han vuelto parte del léxico cultural.
Y como a la cama no te irás sin saber una cosa más, para complementar la información que acabamos de revisar observa el siguiente video del minuto 2:28 al 3:15.
- Dime que dices y te diré quién eres II
https://www.youtube.com/watch?v=_SugUe0CSoc&t=33s
Tal como se explica en el video, el dicho es una expresión popular que entra como Pedro por su casa y se va formalizando, es decir que se vuelve una frase que no varía por su uso común (por ejemplo, suena raro decir “como Rubén por su casa”), mientras que el refrán es una expresión acompañada de una moraleja.
Aunque estos parezcan sinónimos, los refranes son frases que pertenecen a la cultura popular y presentan de forma indirecta una enseñanza.
- Son sinónimo de los proverbios.
- Presentan una moraleja “oculta”.
- Y se forman a partir de las experiencias de una cultura.
Mientras que los dichos son frases cuyo sentido literal no coincide con su sentido figurado; generalmente hacen referencia a situaciones cotidianas, acompañadas de un toque picaresco y divertido.
- Son sinónimo del término “frase hecha” y pueden popularizarse hasta volverse refranes.
Ambos se preservan dentro de una sociedad por su brevedad y fácil memorización.
Además de estas expresiones populares, existen también los pregones, y como el tiempo es oro observa el siguiente video del minuto 1:10 al 2:47:
- Dime que dices y te diré quién eres I
https://www.youtube.com/watch?v=FIdhdp0RBqg
Ahora sabes que las frases que escuchas comúnmente, como:
- ¡¡El paaaan!!
- ¡¡La leche!!
- ¡¡Lleve sus ricos y deliciosos tamales oaxaqueños!!
Son pregones típicos de México.
Los pregones se crearon para dar a conocer a la comunidad algún servicio o noticia en voz alta.
Anteriormente, los pregoneros oficiales daban avisos del gobierno o la autoridad, ¡¡Extra, extra!! Hoy en día lo más cercano que tenemos a este tipo de pregones son las proclamaciones que se pronuncian a viva voz y de forma repetitiva en la vía pública para anunciar una noticia que ha sido difundida en los medios impresos, algunas veces acompañados de comentarios exagerados para despertar el interés de posibles lectores y aumentar la venta de periódicos.
Además de estos pregoneros, existen también los comerciantes, quienes anuncian su mercancía con un determinado grito o pregón, en algunos casos acompañado de equipos de sonido, grabaciones, música, rima o ritmo musical que resulta fácil recordar y se adopta como tradición popular.
Y el objetivo principal de estas frases es despertar el interés del público y llamar su atención. Estos pregones se caracterizan por utilizar la jerga popular propia del lugar en el que se pronuncian.
Así que si tienes Sombre…ros, zapa…tos o ropa usada que venda, ofrécela a los pregoneros.
Ahora que conoces esta información, lo prometido es deuda, llegó el momento de hacer, deshacer y aprender, al realizar los retos que pondrán a prueba tus conocimientos adquiridos.
Para comenzar lee el siguiente testimonio, pero no me des el avión, pon mucha atención porque después tendrás que seleccionar la respuesta correcta.
“La semana pasada, mi maestra de Lengua Materna nos solicitó realizar un portador textual de manera individual para incluir los cuentos de subgéneros narrativos que mis compañeros y yo escribimos; ella enlistó las características que debía contener el proyecto y estableció una misma fecha de entrega para todos. Mis compañeros comenzaron a trabajar de inmediato y buscaron el material necesario para desarrollar su trabajo.
Yo ocupé mi tarde para ver televisión porque tenía tiempo; restaban dos días más antes de la entrega. La tarde siguiente tomé una siesta y mi tercer día lo ocupé para jugar; estaba tan cansada que sólo pensaba en dormir, pero recordé que la entrega del proyecto tenía que realizarla al día siguiente, y muerta de sueño comencé a elaborar mi portador textual; trabajé gran parte de la noche, pero mi único deseo era poder terminar y descansar.
Dormí sólo 3 horas y me levanté tarde para llegar a la escuela. Cuando entregué mi trabajo, la maestra me hizo ciertas observaciones porque no cumplí con las especificaciones solicitadas; los portadores textuales de mis compañeros estaban muy bien hechos, todos obtuvieron no sólo buenas calificaciones sino felicitaciones por parte de la maestra, se notaba la dedicación y esfuerzo que había puesto en su trabajo.
Al término de la clase, la maestra me mandó llamar y me preguntó los motivos por los cuales no realicé la actividad de manera correcta, yo fui sincera y le expliqué que me confié pensando que tenía mucho tiempo para realizar la actividad, ella me miró con dulzura y me dijo aprende de esta experiencia y…”
Si tú fueras la maestra o maestro… ¿Qué consejo o refrán le darías?
- Aunque la mona vista de seda, mona se queda.
- No dejes para mañana lo que puedes hacer hoy.
- De los cuarenta para arriba, no te mojes la barriga, o
- El saber, no ocupa lugar.
El inciso correcto es B; “No dejes para mañana lo que puedes hacer hoy”.
Y es que en apuros y afanes acude a los refranes.
Ahora observa las siguientes oraciones y relaciona ambas columnas para formar dichos, refranes o pregones.
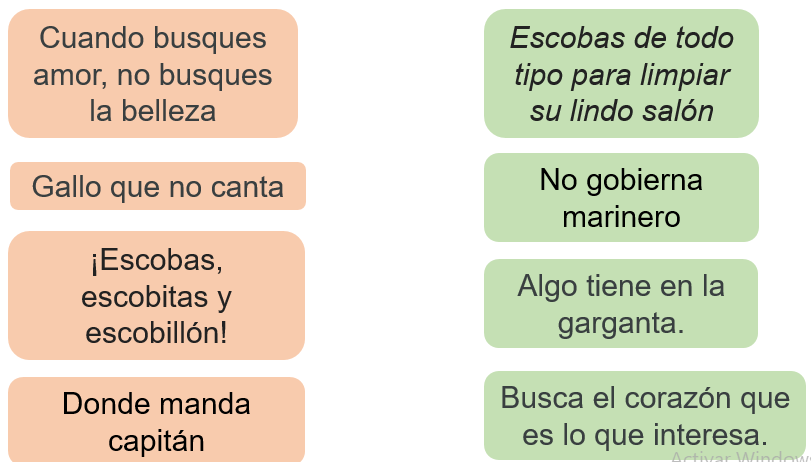
¿Acertaste en tus respuestas? Bueno… El que calla, otorga, así que ahora transcribe las oraciones en tu cuaderno y señala si son refranes, dichos o pregones; explica también a qué se refiere cada enunciado y menciona un ejemplo en el que podrías hacer uso de ellos.
El tiempo se está terminando, pero necesitamos atender y entender para aprender, así que haz un recuento de los conceptos que revisaste durante la sesión:
Los pregones son expresiones que tienen el propósito de invitar a las personas a comprar un producto o usar un servicio. Para conseguir la atención de los clientes los vendedores utilizan frases muy atractivas, de otra manera nadie les prestaría atención en medio de un entorno lleno de sonidos.
Y como aquí todo el contenido es bueno, bonito y barato, revisa qué son los dichos.
Los dichos son expresiones que describen una situación de manera ingeniosa y de forma metafórica o figurada. Los usas para hacer que nuestras palabras resulten significativas.
Y ya que estas hablando sin pelos en la lengua… Los refranes son frases que expresan un consejo o pensamiento moral que se repiten de manera invariable. Cada pueblo tiene sus propios refranes y éstos se transmiten de boca en boca para formar parte de una identidad. Al buen entendedor pocas palabras.
Escribe y responde en tu cuaderno las siguientes preguntas:
- ¿Qué es un pregón, un dicho y un refrán?
- ¿Cómo se distingue uno de otro?
- ¿En qué casos se utiliza cada uno?
- ¿Dónde los han escuchado?
- ¿Quiénes los dicen?
- ¿Ustedes cuáles conocen?
- Y ¿cuál es la diferencia entre lenguaje literal o significado explícito y lenguaje metafórico o significado implícito?
Si desconoces alguna respuesta, puedes revisar los apuntes que realizaste durante la sesión o consultar tus dudas con su maestra o maestro, recuerda que el que busca, encuentra.
Recopila y escribe en tu cuaderno los refranes, dichos o pregones que estuviste leyendo durante el desarrollo de la sesión
Sin darte cuenta, de manera continua escuchas o utilizas ciertas frases para comunicarte y relacionarte con otras personas con fines muy variados, como comprar y vender productos, expresar lo que ocurre en el mundo de forma figurada o metafórica o dar un consejo o enseñanza.
Algunas situaciones se repiten con frecuencia. Así las comunidades han aprendido a emplear dichos, refranes y pregones en determinados momentos; así que, para conocer la definición, características y diferencias entre estos conceptos, te invito a echarte un taco de ojo con toda la información que revisarás a continuación.
Los dichos son enunciados que contienen ciertas ocurrencias ingeniosas que se expresan en sentido figurado.
Es decir, con palabras que adquieren un significado distinto al contexto, que no coinciden literalmente con lo que expresan, sino que ilustran una idea o concepto utilizando recursos retóricos, como la metáfora o la ironía.
Por ejemplo, “salvado por la campana” es una frase que se utiliza cuando gracias a que algún suceso se interpone en tus actividades, dejas de realizar una acción que te aburre o desagrada.
Esta es una frase derivada del boxeo y se documenta a principios del siglo XX, y se refiere, por supuesto, al hecho de que la campana marca el final de un round y sirve para tener un minuto de descanso para los boxeadores, lo cual beneficia, particularmente, a aquel que esté siendo más atacado. Así nació el significado de esta frase.
Los dichos también son denominados “expresiones populares” con sonoridad y rima que dan un sentido divertido a nuestras expresiones cotidianas; son una forma de entender la vida a través de analogías sobre diversos temas que se transmiten de generación en generación, y por ser el resultado de años de experiencia son considerados patrimonio de la humanidad.
Otro ejemplo de este tipo de expresiones es: ¡Ya nos cayó el chahuistle! Esta frase tan peculiar es utilizada cuando te sorprenden haciendo algún acto indebido o cuando una persona desagradable se agrega a los planes sin ser requerida.
En México se le nombra chahuistle a una enfermedad producida por un hongo que afecta los cultivos del maíz. Es un término de origen náhuatl “chahuiztli”, que significa “enfermedad de la hoja del maíz”, y que durante cientos de años devastó los cultivos de las comunidades prehispánicas, no hay que olvidar que en la época prehispánica el maíz era parte importante en la economía y tradiciones mesoamericanas, para proteger sus cultivos surgieron rituales, no obstante, el hongo seguía invadiendo la siembra causando desgracias. Así es como surge esta expresión.
Pero ya le echaste mucha crema a los tacos, aprende lo qué son los refranes..
Los refranes son frases que expresan sabiduría popular a través de un consejo o enseñanza en forma metafórica, utilizando palabras distintas a las de uso común para representar la realidad. Su propósito es educativo, hacen referencia a situaciones que cualquier persona puede enfrentar y se transmiten de generación en generación sin importar el origen, las costumbres, la edad o la forma de vida.
Y los antecedentes de los refranes son los proverbios; en la antigüedad, éstos hacían referencia a hechos históricos, costumbres, supersticiones, actividades o personajes célebres de esa época, hoy en día es una tradición oral que se ha mantenido vigente en todo el mundo. Los españoles los consideraban “filosofía popular" por ser enunciados sabios y verdaderos de uso común.
Transmitir los refranes, tradicionalmente de generación en generación, ocasiona que estos puedan sufrir algunas variaciones con el tiempo; por ejemplo, el refrán “perro ladrador poco mordedor” es ahora conocido como “perro que ladra no muerde”. La idea es la misma pero la rima ha desaparecido y la moraleja hace referencia a las personas que gritan mucho o amenazan, pero no cumplen lo dicho con palabras.
Los refranes, al igual que los dichos, no pueden ser tomados de manera literal. Por lo tanto, pueden expresar dos sentidos, uno explícito que resulta fácil de entender por la forma en que está escrito y otro implícito donde debes buscar el significado real, por ejemplo:
El refrán: “Camarón que se duerme se lo lleva la corriente”, en el sentido explícito explica que cuando un camarón está despierto tiene la capacidad de sujetarse bien al fondo del mar, pero cuando éste se descuida o se duerme, la corriente lo arrastrará. En el sentido implícito, el significado de este refrán hace referencia a que si una persona se descuida (se "duerme" en este caso), puede meterse en problemas o salir afectado ("arrastrado por la corriente").
Otros ejemplos de refranes explícitos son:
- El que espera, desespera.
- Hoy por ti, mañana por mí.
- Más vale tarde que nunca.
- Haz el bien sin mirar a quién.
En estos enunciados no necesitas dar una explicación implícita, porque las palabras que utilizas al expresarlos facilitan la comprensión.
Otra característica importante de los refranes es el uso de recursos literarios como la rima, tanto asonante como consonante. La rima es la repetición de sonidos vocálicos y consonánticos, o sólo vocálicos, a partir de la última vocal acentuada en dos o más versos.
Una rima asonante es aquella en la que sólo coinciden los sonidos de las vocales, por ejemplo: “cuanto más se tiene más se quiere”.
La rima consonante es aquella en la que coinciden los sonidos de la última vocal acentuada incluyendo las vocales y las consonantes, por ejemplo: “a lo hecho pecho”.
Los refranes escritos en verso tienen cierto ritmo y resultan más fáciles de recordar; por lo tanto, son aquellos que se han vuelto parte del léxico cultural.
Y como a la cama no te irás sin saber una cosa más, para complementar la información que acabamos de revisar observa el siguiente video del minuto 2:28 al 3:15.
- Dime que dices y te diré quién eres II
https://www.youtube.com/watch?v=_SugUe0CSoc&t=33s
Tal como se explica en el video, el dicho es una expresión popular que entra como Pedro por su casa y se va formalizando, es decir que se vuelve una frase que no varía por su uso común (por ejemplo, suena raro decir “como Rubén por su casa”), mientras que el refrán es una expresión acompañada de una moraleja.
Aunque estos parezcan sinónimos, los refranes son frases que pertenecen a la cultura popular y presentan de forma indirecta una enseñanza.
- Son sinónimo de los proverbios.
- Presentan una moraleja “oculta”.
- Y se forman a partir de las experiencias de una cultura.
Mientras que los dichos son frases cuyo sentido literal no coincide con su sentido figurado; generalmente hacen referencia a situaciones cotidianas, acompañadas de un toque picaresco y divertido.
- Son sinónimo del término “frase hecha” y pueden popularizarse hasta volverse refranes.
Ambos se preservan dentro de una sociedad por su brevedad y fácil memorización.
Además de estas expresiones populares, existen también los pregones, y como el tiempo es oro observa el siguiente video del minuto 1:10 al 2:47:
- Dime que dices y te diré quién eres I
https://www.youtube.com/watch?v=FIdhdp0RBqg
Ahora sabes que las frases que escuchas comúnmente, como:
- ¡¡El paaaan!!
- ¡¡La leche!!
- ¡¡Lleve sus ricos y deliciosos tamales oaxaqueños!!
Son pregones típicos de México.
Los pregones se crearon para dar a conocer a la comunidad algún servicio o noticia en voz alta.
Anteriormente, los pregoneros oficiales daban avisos del gobierno o la autoridad, ¡¡Extra, extra!! Hoy en día lo más cercano que tenemos a este tipo de pregones son las proclamaciones que se pronuncian a viva voz y de forma repetitiva en la vía pública para anunciar una noticia que ha sido difundida en los medios impresos, algunas veces acompañados de comentarios exagerados para despertar el interés de posibles lectores y aumentar la venta de periódicos.
Además de estos pregoneros, existen también los comerciantes, quienes anuncian su mercancía con un determinado grito o pregón, en algunos casos acompañado de equipos de sonido, grabaciones, música, rima o ritmo musical que resulta fácil recordar y se adopta como tradición popular.
Y el objetivo principal de estas frases es despertar el interés del público y llamar su atención. Estos pregones se caracterizan por utilizar la jerga popular propia del lugar en el que se pronuncian.
Así que si tienes Sombre…ros, zapa…tos o ropa usada que venda, ofrécela a los pregoneros.
Ahora que conoces esta información, lo prometido es deuda, llegó el momento de hacer, deshacer y aprender, al realizar los retos que pondrán a prueba tus conocimientos adquiridos.
Para comenzar lee el siguiente testimonio, pero no me des el avión, pon mucha atención porque después tendrás que seleccionar la respuesta correcta.
“La semana pasada, mi maestra de Lengua Materna nos solicitó realizar un portador textual de manera individual para incluir los cuentos de subgéneros narrativos que mis compañeros y yo escribimos; ella enlistó las características que debía contener el proyecto y estableció una misma fecha de entrega para todos. Mis compañeros comenzaron a trabajar de inmediato y buscaron el material necesario para desarrollar su trabajo.
Yo ocupé mi tarde para ver televisión porque tenía tiempo; restaban dos días más antes de la entrega. La tarde siguiente tomé una siesta y mi tercer día lo ocupé para jugar; estaba tan cansada que sólo pensaba en dormir, pero recordé que la entrega del proyecto tenía que realizarla al día siguiente, y muerta de sueño comencé a elaborar mi portador textual; trabajé gran parte de la noche, pero mi único deseo era poder terminar y descansar.
Dormí sólo 3 horas y me levanté tarde para llegar a la escuela. Cuando entregué mi trabajo, la maestra me hizo ciertas observaciones porque no cumplí con las especificaciones solicitadas; los portadores textuales de mis compañeros estaban muy bien hechos, todos obtuvieron no sólo buenas calificaciones sino felicitaciones por parte de la maestra, se notaba la dedicación y esfuerzo que había puesto en su trabajo.
Al término de la clase, la maestra me mandó llamar y me preguntó los motivos por los cuales no realicé la actividad de manera correcta, yo fui sincera y le expliqué que me confié pensando que tenía mucho tiempo para realizar la actividad, ella me miró con dulzura y me dijo aprende de esta experiencia y…”
Si tú fueras la maestra o maestro… ¿Qué consejo o refrán le darías?
- Aunque la mona vista de seda, mona se queda.
- No dejes para mañana lo que puedes hacer hoy.
- De los cuarenta para arriba, no te mojes la barriga, o
- El saber, no ocupa lugar.
El inciso correcto es B; “No dejes para mañana lo que puedes hacer hoy”.
Y es que en apuros y afanes acude a los refranes.
Ahora observa las siguientes oraciones y relaciona ambas columnas para formar dichos, refranes o pregones.

¿Acertaste en tus respuestas? Bueno… El que calla, otorga, así que ahora transcribe las oraciones en tu cuaderno y señala si son refranes, dichos o pregones; explica también a qué se refiere cada enunciado y menciona un ejemplo en el que podrías hacer uso de ellos.
El tiempo se está terminando, pero necesitamos atender y entender para aprender, así que haz un recuento de los conceptos que revisaste durante la sesión:
Los pregones son expresiones que tienen el propósito de invitar a las personas a comprar un producto o usar un servicio. Para conseguir la atención de los clientes los vendedores utilizan frases muy atractivas, de otra manera nadie les prestaría atención en medio de un entorno lleno de sonidos.
Y como aquí todo el contenido es bueno, bonito y barato, revisa qué son los dichos.
Los dichos son expresiones que describen una situación de manera ingeniosa y de forma metafórica o figurada. Los usas para hacer que nuestras palabras resulten significativas.
Y ya que estas hablando sin pelos en la lengua… Los refranes son frases que expresan un consejo o pensamiento moral que se repiten de manera invariable. Cada pueblo tiene sus propios refranes y éstos se transmiten de boca en boca para formar parte de una identidad. Al buen entendedor pocas palabras.