SEC1-FCE-09MAR

 

FORMACIÓN CÍVICA Y ÉTICA - SECUNDARIA 1

Cuando la ley manda, la fuerza calla

(MARTES 09 MARZO)

ACTIVIDAD:

Se te recomienda que veas dos películas, la primera de ellas Philadelphia del director Jonathan Demme, y la segunda Cuestión de honor del director Rob Reiner; ambos filmes tratan sobre la búsqueda de la justicia, seguro te encantarán.

 

Concluye también el cuadro de los ámbitos que revisaste en el desarrollo de esta sesión.

RESUMEN:

Es frecuente leer y escuchar acerca de cuestiones de derecho o justicia: “que si esto es justo, que si está apegado a derecho, que si es legal…”; y, además, se piensa que se trata de cuestiones aburridas y difíciles de comprender; sin embargo, en esta sesión tienes la oportunidad de darte cuenta de que no es así.

Se irá paso a paso. Sabes ¿qué es el derecho? No, no sólo es un adjetivo o un camino, comienza a pensar qué más es.

 

Escucha la respuesta de algunas y algunos ciudadanos cuando se les preguntó: ¿qué es el derecho?

 

FCYE1_B2_SEM26_PG1_AUDIO 1. https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202103/202103-RSC-SqeezmgKRX-1-FCYE1_B2_SEM26_P1_AUDIO1.m4a	A mí me parece que es como un grupo de leyes que sirven para que haya una buena convivencia entre todos.
FCYE1_B2_SEM26_PG1_AUDIO 2 https://aprendeencasa.sep.gob.mx/multimedia/RSC/Video/202103/202103-RSC-ENC81E7bqv-2.FCYE1_B2_SEM26_P1_AUDIO2.mp4	El derecho, es el conjunto de normas que regulan las relaciones entre los individuos pertenecientes a una sociedad determinada.   Y a nivel macro es un conjunto de normas que regulan las relaciones entre las naciones.
FCYE1_B2_SEM26_PG1_AUDIO 3. https://aprendeencasa.sep.gob.mx/multimedia/RSC//202103/202103-RSC-J57bwWYgvG-3.FCYE1_B2_SEM26_P1_AUDIO3.ogg	¿Qué significa para mí el derecho? Para mí significa un conjunto de normas que imponen deberes y reglas que confieren ciertas facultades que entablan la convivencia social y cuyo objetivo es generar valores: seguridad, certeza, igualdad, libertad y justicia.

 

Como pudiste darte cuenta, todas y todos tienen una noción del concepto, pero sólo eso. Para ahondar en su conocimiento y el tuyo, se dirá que el término derecho proviene del latín directum y significa “rígido” o “recto”, pero también se refiere al conjunto de normas jurídicas (leyes) que regulan las relaciones entre particulares, o entre particulares y el gobierno para que las relaciones entre todas las personas sean armónicas y pacíficas.

 

Pero, ¿cuál es la relación del derecho con la justicia?

 

Pues bien, el derecho y la justicia son dos términos que siempre van de la mano. ¿Sabes qué es la justicia?

 

Piensa en ello mientras escuchas lo que dijeron las y los ciudadanos entrevistados. Anota en tu cuaderno dichos conceptos, y las ideas expresadas que consideres que te van a permitir generar tu propia definición de justicia, pues estarás trabajando sobre derecho y justicia todavía por un buen rato.

 

FCYE1_B2_SEM26_PG1_AUDIO 4 https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202103/202103-RSC-JuFXDT2Kc1-4.FCYE1_B2_SEM26_P1_AUDIO4.m4a	Yo creo que la justicia, es que todos tengan los mismos derechos y que se castigue a quienes no cumple la ley.
FCYE1_B2_SEM26_PG1_AUDIO 5. https://aprendeencasa.sep.gob.mx/multimedia/RSC/Video/202103/202103-RSC-4BXRfoBySt-5.FCYE1_B2_SEM26_P1_AUDIO5.mp4	La justicia en su definición literal implica lo justo, esto es, en una sociedad, es dar a cada uno, lo que le pertenece o lo que le corresponde y normalmente es sinónimo de equidad.

 

 

Como pudiste escuchar, las y los participantes también tienen una noción de lo que es la justicia. Sin embargo, puede ser más puntual y profunda. Se hará un poquito de historia para ampliar tu saber acerca de ella.

 

El término “justicia” fue definido, por primera vez, por Ulpiano, un jurista romano que vivió en el siglo II de esta era. Ulpiano definió la justicia como “la voluntad firme y continuada de dar a cada quien lo suyo”.

 

Si analizas con cuidado el concepto, puedes darte cuenta de que aún sigue vigente, ya que, por el simple hecho de ser personas, todas y todos gozan de los mismos derechos, los cuales han sido llamados humanos, como lo son el derecho a la educación, a vivir una vida libre de violencia o a la salud, entre otros.

Ahora bien, es importante que tengas en cuenta que los conceptos de derecho y justicia varían según el tiempo y el espacio en el que se definan; es decir, no eran considerados de la misma forma durante la Edad Media que en la actualidad; o en Medio Oriente que en México. Incluso, dentro del país el significado puede variar si se aplica en una comunidad indígena que se rige por sus usos y costumbres, que en las zonas urbanas que se rigen por las normas y leyes locales o federales.

 

Observa el siguiente ejemplo que retrata la situación en una comunidad.

 

6. Usos y costumbres.

https://www.youtube.com/watch?v=Ad0JPnOb-Fg

Revisa del tiempo: 3:24 al 4:34.

 

Como observaste, los usos y costumbres pueden normar la vida de una persona, una familia y una comunidad y provocar actos de injusticia, como el caso de la adolescente del video, pero que se pueden resarcir o reparar. Es necesario aclarar que la justicia no se hace o no se lleva a cabo por sí sola, sino que es necesario que la ejecuten. ¿Quiénes? Por supuesto que los individuos que conforman una sociedad.

 

Es decir, la justicia tiene que ser más que un concepto, una acción que se lleve a cabo en todos los niveles, desde la familia, la escuela, la comunidad, el país y entre las naciones.

Para que esto te pueda quedar más claro, pon atención al siguiente video, en el que se plantea una situación injusta; identifica cuál fue el mecanismo que permitió reparar el daño.

 

7. Justicia.

https://youtu.be/74fmSx9g2Vg

 

¿Qué te pareció el cuento La futbolista? ¿Identificaste cómo se relacionan la igualdad y la justicia?, ¿y cómo se procura la legalidad para lograr la justicia?

 

Es interesante que a Luis no sólo le gustará ver, sino actuar y practicar tanto el futbol como la justicia y la igualdad.

¿Tomaste nota de que Macarena recurrió al reglamento para luchar por su inclusión al equipo?

 

Eso demuestra que las normas pueden ser una excelente herramienta para la procuración de justicia. Generalmente, a la justicia se le representa con una balanza, como la que ves ahora en la siguiente imagen.

 

 

También lo hacen con una mujer con los ojos vendados que sostiene la balanza con una mano, esto significa que la justicia es igual para todas y todos y que no debe existir favoritismos ni preferencias por razón del sexo, género, posición económica, etnia, ni por ninguna otra causa. Con la otra sostiene una espada que significa que la justicia se aplicará con todo el peso de la ley.

 

 

Hay que hacer un alto para destacar que, a lo largo de la historia, han existido leyes que no han sido del todo justas; por ejemplo, aquellas que prohibían el voto de las mujeres en las elecciones, o el derecho que se les otorgaba a los papás para “corregir” a sus hijas e hijos por medio de los castigos corporales.

 

Como recordarás, al inicio de esta sesión se mencionó que las normas o leyes sirven para regular las relaciones entre personas o naciones; es decir, habrá normas o reglas en todos los contextos en los que te estés desenvolviendo.

 

Así, en tu familia existen reglas, tales como que todas y todos colaboren en los quehaceres de casa o que no se podrá jugar si no has hecho la tarea. En casa quienes aplican esas normas son tus padres o tutores y, en caso de no respetarlas, te haces acreedor a una sanción.

 

En la escuela debes guardar silencio en las ceremonias cívicas o no maltratar física o verbalmente a ninguna de las compañeras, compañeros o docentes, ya que, en caso de hacerlo, tendrás también una sanción conocida como medida disciplinaria, en apego al Marco para la Convivencia Escolar, expedido por la Secretaría de Educación Pública.

 

En tu comunidad también existen reglas o normas que debes seguir para tener una convivencia armónica; por ejemplo, si sacas a pasear a tu mascota debes recoger las heces fecales para no molestar a tus vecinas y vecinos ni dañar el medio ambiente y, en caso de no hacerlo, podrán multarte por haber cometido una infracción a la Ley de Cultura Cívica de la Ciudad de México.

 

Como podrás darte cuenta, en todos los espacios de convivencia existen normas que propician una interacción pacífica y armónica entre todas y todos.

 

Recapitulando lo que has estudiado hasta ahora. En tu cuaderno elabora un cuadro, divídelo en tres columnas. En la primera columna anota el ámbito de convivencia, en la segunda columna pon ejemplos de conducta y, en la tercera, normas que las regulan.

 

Pon cuatro filas abajo del primer ámbito colocando en cada una: familiar, escolar, laboral y social. Anota ejemplos de conductas y normas que regulan cada ámbito.

 

 

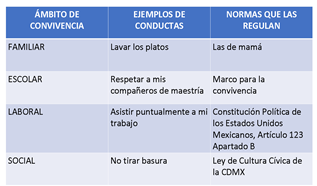
Por ejemplo, en la columna de ámbito familiar, se describe una conducta que es lavar los platos y en la columna de las normas que las regulan son las de mamá. Sigue completando el cuadro y anotando los diferentes ámbitos en que se desenvuelven los ejemplos de conducta y las normas que las regulan.

 

Entonces, se puede afirmar que las leyes son justas y permiten una sana convivencia entre los seres humanos. Sin embargo, aquel que las incumpla será sancionado por romper con la armonía y sana convivencia social.

 

Pero, ¿es suficiente con sancionar a quien incumplió la ley?

 

La respuesta es que, no basta con sancionar a quien violenta la tranquilidad o la seguridad de otra u otro.

 

Es necesario pensar que quien ha sido víctima del incumplimiento de una norma necesita que ese daño sea reparado. Y es entonces cuando surgen dos conceptos de suma importancia: la justicia conmutativa y la reparación del daño.

 

La justicia conmutativa se presenta entre particulares, que no son ni actúan como autoridades, pero tiene como fin llegar a acuerdos de manera pacífica para la resolución de un conflicto en el cual ambas partes quedan conformes sin que una de ellas obtenga ventaja alguna, sino que obtienen el mismo grado o nivel de satisfacción.

Por ejemplo, la compra-venta de un auto, en el cual ambas partes están de acuerdo en el precio y las características del vehículo.

 

En el caso de la reparación del daño, el infractor tendrá la obligación de volver a dejar las cosas en el estado en que se encontraban antes de que realizara su conducta y las cambiara o destruyera, además de pagar por los daños que le causó a la víctima.

 

Por ejemplo, alguien que al podar un árbol lesiona a otra persona que iba pasando por el lugar cuando serruchaba las ramas tendrá que pagar los gastos médicos por las curaciones y pagarle un dinero extra por los días que no pudo ir a trabajar por la lesión.

 

Si se habla de sanciones, éstas tendrán que estar contempladas en las leyes, las cuales, a su vez, deberán respetar la dignidad y los derechos humanos de todas las personas, sean víctimas o infractores.

Es decir, las leyes están sustentadas en los derechos humanos, los cuales como recordarás tienen sus antecedentes en la Declaración de los Derechos del Hombre y del Ciudadano, emitida en Francia en 1789 durante la Revolución francesa.

 

Esta sesión ha sido muy productiva y por ello es recomendable continuar tu reflexión con base en los siguientes puntos:

 

• La justicia es un valor, una virtud y un ideal que busca la equidad.
• Los actos injustos se pueden revertir cuando se reparan los daños.
• Las normas y leyes son instrumentos para promover la equidad y, por lo tanto, la justicia.
• Las normas y leyes se aplican para el logro de una convivencia justa.

 

Has llegado al final de la sesión.

SEC1-MAT-09MAR

 

MATEMÁTICAS - SECUNDARIA 1

Tríadas de medidas

(MARTES 09 MARZO)

ACTIVIDAD:

Revisa tu libro de texto, seguramente encontrarás situaciones similares a las vistas que resultarán enriquecedoras.

RESUMEN:

Para comenzar, se jugará al telegrama, para ello se describirá de qué se trata:

El juego consiste en enviar un telegrama a una persona describiendo las características de una figura para que la trace.

 

Una característica de los telegramas, es que tienen una cantidad restringida de palabras por mensaje, en el juego debes utilizar 30 palabras, como máximo, para indicar las características de la figura que se debe trazar. Ten a la mano lápiz y papel para que copies el siguiente formato del telegrama:

 

 

En la parte superior derecha lleva la fecha. Abajo va el domicilio del destinatario y después su nombre. En seguida, tiene el espacio para escribir el mensaje y, en la parte inferior, el nombre de quien envió el telegrama.

 

¿Lo tienes anotado?

 

Ya sabes que el mensaje no debe llevar más de 30 palabras. Pero hay que considerar que los números con unidades se cuentan como una palabra por ejemplo 3 centímetros, 45 grados, cuentan como una palabra.

 

Revisa un ejemplo para poder entender mejor el juego.

 

30 palabras máximo. Poder reproducir el triángulo a la perfección.   3cm, una palabra.   45°, una palabra.

 

Los datos como la fecha, el domicilio, destinatario, y remitente (quien envía) no se cuentan dentro de las 30 palabras.

Revisa el mensaje que trae los datos para trazar dos triángulos.

 

 

Se lee:

Trazar los triángulos, ahí van 3 palabras.

Debajo dice: T1 medidas: que cuenta como dos palabras, después medidas: 3 centímetros, 3 centímetros, 3 centímetro, 60 grados, 60 grados y 60 grados, obteniendo un total de 8 palabras. Los signos de puntuación no se cuentan.

 

En el siguiente renglón, se señala la información, T2 medidas: 6 centímetros, 45 grados, 6 centímetros, 45 grados, 8 punto 45 centímetros y por último 90 grados, otras 8 palabras.

 

Al sumar se tienen 19 palabras, por lo que se cumplió con la regla de usar máximo 30 palabras.

 

La persona que recibió el mensaje, que fue Luis Adrián, ya tiene los elementos suficientes para trazar los triángulos que se le pidieron. Revisa sus respuestas:

 

Luis describió los pasos que siguió para trazar las figuras.

 

Para el primer triángulo dibujó un segmento de 3 centímetros, en uno de sus extremos trazó un ángulo de 60 grados y sobre uno de sus lados, puso una marca de 3 centímetros. Volvió a marcar un ángulo de 60 grados y lo extendió para cerrar el triángulo.

 

Para el segundo triángulo, trazó un lado de 6 cm y un ángulo de 90 grados y sobre el otro lado del ángulo, otro lado de 6 cm; después midió y trazó un ángulo de 45 grados y el otro lado de 8.45 cm y con esto se cerró el triángulo, formando el segundo ángulo de 45 grados.

 

Ahora, ya tienes el formato para escribir tu telegrama, y también tienes idea de cómo se cuentan las palabras, recuerda de no pasarte de 30. ¿Lista o listo?

 

Observa la siguiente imagen con varios triángulos de los que hay que enviar información. Anota los valores, para que después, puedas hacer tu telegrama, no es necesario que copies las figuras.

 

 

Considera las medidas de cada triángulo:

 

• Primer triángulo, T1, lados, 3, 4 y 5 centímetros, respectivamente; ángulos 53 grados, 90 grados y 37 grados.

 

• Segundo triángulo, T2, lados: 5 cm, 5 cm y 9 cm; ángulos: 25 grados, 130 grados y 25 grados.
• Tercer triángulo, T3, lados: 3 cm, 3 cm y 2.5 cm; ángulos: 65 grados, 50 grados y 65 grados.

 

• Cuarto triángulo, T4, lados: 7.8 cm, 4 cm, 7.5 cm; ángulos: 30 grados, 70 grados y 80 grados.

 

• Quinto triángulo, T5, lados: 9.2 cm, 4 cm, 7 cm; ángulos: 24 grados, 46 grados y 110 grados.

 

• Sexto y último triángulo, T6, lados: 6.1 cm, 7.9 cm y 4 cm; ángulos: 100 grados, 30 grados y 50 grados

 

Tomaste nota, ¿verdad?

 

¿Será posible escribir todos los datos de todos los triángulos en un mismo telegrama? Recuerda que no puedes pasarte de 30 palabras. ¿Cuántos triángulos podrías enviar incluyendo todos tus datos?

 

Si anotaste todas las medidas, de lados y ángulos de un sólo triángulo, necesitas como mínimo 6 palabras y, si eso lo multiplicas por 6 triángulos, te excederías del número de palabras permitidas.

 

Reflexiona: ¿Habrá una forma de omitir datos en el telegrama de manera que quien lo recibe pueda construir los triángulos solicitados? ¿Tienes alguna estrategia?

 

Para responder lo anterior y saber si es posible enviar el telegrama incluyendo todos los triángulos, se retomará el ejemplo del primero de ellos.

 

Para trazar el triángulo, sabiendo que todos sus lados miden 3 cm y sus ángulos 60 grados, primero se traza un lado de 3 centímetros, a continuación, en un extremo se traza un ángulo de 60 grados, sobre el segundo lado del ángulo, se mide y se pone una marca a los 3 cm y se une el segmento inicial con el punto señalado para formar el triángulo. Observa que los triángulos obtenidos son iguales, es decir, son congruentes. Ahora la pregunta es: ¿cuántos datos fueron necesarios para trazar el segundo triángulo?

 

 

Observa que ya no fueron necesarios los datos de los otros dos ángulos ni del tercer lado; esto quiere decir que, con sólo 3 datos del triángulo, puedes reproducir uno congruente al que se describió en el telegrama. ¿Identificaste qué datos son? ¿Cómo se relacionan entre ellos?

 

Recuerda que dos figuras son congruentes cuando las medidas de sus lados y de sus ángulos correspondientes son iguales.

 

Revisa la siguiente situación.

 

Considera que tienes un ángulo de 60 grados y un segmento que mide 3 centímetros, para trazar un triángulo; y para otro, tienes la medida de dos lados, uno de 3 cm y el otro de 2 cm. ¿Con estos datos es posible construir un único triángulo, en cada caso?

 

Si construyes triángulos de manera que cumplan con estos datos, ¿considera que tus compañeras y compañeros trazarían triángulos congruentes a los tuyos? Analiza los datos y trazos que hicieron dos estudiantes.

 

Ellos trazaron un triángulo considerando la siguiente información: un ángulo de 60 grados y un lado de 3 cm. El primero, trazó un triángulo escaleno con un lado de 3 cm y un ángulo de 60 grados; y el segundo, trazó un triángulo equilátero. Ambos cumplieron con las condiciones dadas.

 

Ahora, considera las medidas para el otro triángulo que son dos lados, 3 cm y 2 cm. Nuevamente, dos estudiantes trazaron su triángulo.

 

 

Observa que ambos cumplieron con la condición, pero uno trazó un triángulo rectángulo y el otro uno obtusángulo, por lo que sus triángulos no son congruentes.

 

Con lo anterior, se puede asegurar que, para construir un único triángulo, considerando ciertos datos, se necesitan más de dos medidas.

 

Ahora, continuando con el juego, revisa el siguiente telegrama, donde se muestran las medidas para trazar 6 triángulos. En este caso, para cumplir con el límite de 30 palabras, se omitieron algunas medidas. Toma nota de las medidas e intenta reproducir las figuras y las compararás con otras figuras para ver qué sucede.

 

En el telegrama se tiene la información para trazar 6 triángulos. En todos los casos, únicamente se dan tres medidas.

Triángulo 1: 3 centímetros, 3 centímetros y 3 centímetros.

Triángulo 2: 5 centímetros, 9 centímetros y 4 centímetros.

Triángulo 3: 30 grados, 9 centímetros y 45 grados.

Triángulo 4: 80 grados, 7 centímetros y 100 grados.

Triángulo 5: 45 grados, 50 grados y 85 grados.

Triángulo 6: 8 centímetros, 30 grados, 10 centímetros.

 

¿Ya tienes las medidas registradas?

 

Ahora, tienes que reproducir los triángulos, considerando únicamente los tres datos dados en cada figura. Verificarás si, con esas medidas, se pueden construir triángulos únicos; es decir, triángulos congruentes.

 

Para construir los triángulos 1 y 2, únicamente tienes las medidas de los tres lados. Para trazarlos, usarás regla y compás. Observa:

 

 

Para el triángulo 1, primero trazas un segmento de 3 centímetros. Abres el compás a 3 centímetros y, con el centro en un extremo del segmento anterior, trazas una circunferencia Repites lo anterior desde el otro extremo del segmento de 3 centímetros. La abertura del compás representa la medida de los otros lados del triángulo. Señalas uno de los puntos donde se cortan las circunferencias, éste señalará el tercer vértice. Unes dicho punto con los extremos del segmento y obtienes tu triángulo.

 

Ahora, siguiendo el mismo procedimiento, intenta trazar el triángulo de lados 9, 5 y 4 centímetros. Trazas el segmento de 9 centímetros, abres el compás a 5 centímetros y con el centro en un extremo del segmento de 9 centímetros, trazas un arco de circunferencia. A continuación, abres el compás a 4 centímetros y trazas un arco de circunferencia desde el otro extremo del segmento.

 

 

Observa que los arcos de circunferencia no se cortan; sólo se tocan en un punto, por ello no se puede trazar un triángulo de 9, 5 y 4 cm de lado. Esta información es muy importante, ya que demuestra que un triángulo no puede ser construido con cualquier triada de longitudes o medidas. Esto te lleva a la condición que dice: “La suma de las medidas de cualquier par de lados en un triángulo, debe ser mayor que la medida del tercer lado”, y en el ejemplo puedes ver que 4 más 5 es igual que 9, por lo que no se cumple la condición mencionada.

 

Ya viste que el triángulo 2 no se pudo construir, ahora analiza al triángulo 1 ¿Cuántos triángulos diferentes piensas que se pueden trazar?

 

Observa que, para construir un triángulo dados sus tres lados, sólo hay una manera de colocarlos, aunque la posición del triángulo puede cambiar, como se ve.

 

Ahora se intentará construir el triángulo 3 del telegrama, cuyas medidas conocidas son: un ángulo de 30 grados, un lado de 9 centímetros y otro ángulo de 45 grados.

Toma tu transportador y regla para realizar el trazo.

 

 

Primero, con el transportador, trazas el ángulo de 30 grados; enseguida, a partir de su vértice y uno de sus lados, mide con la regla y traza el lado de 9 cm, y en el extremo del segmento trazado, marcas el ángulo de 45 grados.

 

Por último, prolongas los lados de los ángulos hasta que se crucen para formar el triángulo. Con estas medidas y en ese orden, ¿se podrán formar diferentes triángulos o todos serán congruentes?

 

Repite varias veces los trazos para construir diferentes triángulos, con las medidas anteriores y verifica si todos son congruentes.

 

Analiza el cuarto triángulo, tienes dada la misma información y en el mismo orden, ésta es: 80 grados, 7 centímetros y 100 grados. La pregunta es, ¿será posible construir el triángulo? Observa la siguiente imagen.

 

Se siguen los mismos pasos que en el caso anterior, pero algo pasó que, en este caso, no se puede trazar el triángulo. ¿Identificaste por qué?

 

Efectivamente, aunque realizaste los trazos correctamente, la posición y medida de los ángulos no permite que se crucen sus lados.

 

Lo anterior, se debe a la propiedad que muestran todos los triángulos, que debes recordar y dice que: “la suma de los ángulos interiores de cualquier triángulo es igual a 180º”. Y, en el caso anterior, sólo dos ángulos suman esa medida: 80 grados + 100 grados = 180 grados.

 

 

Recapitulando:

 

Viste que, para construir un triángulo, una condición es que la suma de las medidas de dos de sus lados debe ser mayor a la medida del tercer lado y también que la suma de sus ángulos interiores siempre es de 180º.

 

También revisaste que, para construir un triángulo que cumpla con ciertas medidas, no es necesario conocer todas ellas, únicamente necesitas tres datos. Con la medida de sus 3 lados; con la medida de 2 lados y el ángulo entre ellos y también, con la medida de dos ángulos y el lado entre ellos es suficiente. En todos estos casos, todos los triángulos correspondientes serán congruentes.

 

Aún falta construir los triángulos 5 y 6 del telegrama. En el caso del triángulo 5 las medidas son: 45 grados, 50 grados y 85 grados.

 

Con estos datos, ¿todos los triángulos construidos serán congruentes o pueden ser diferentes?

 

Revisa los triángulos que trazaron unos estudiantes.

 

 

Los tres triángulos tienen las mismas medidas de sus ángulos, aunque es evidente que sus tamaños son distintos. Esto sucede porque determinar ángulos iguales, no garantiza construir triángulos congruentes, en estos casos, únicamente tienen lados correspondientes iguales.

 

Únicamente falta el triángulo 6. Las medidas dadas son: 8 centímetros, 30 grados y 10 centímetros. Con estas medidas, ¿cómo serán todos los triángulos que se construyan?

Observa lo que hicieron tres estudiantes.

 

El primero, trazó el ángulo de 30 grados, después el lado de 8 centímetros; en el extremo de éste, opuesto al ángulo de 30 grados, trazó el lado de 10 centímetros y unió el extremo del segmento con el vértice del ángulo.

 

El segundo estudiante siguió un procedimiento similar: trazó el ángulo de 30 grados y el lado de 10 centímetros y, del lado opuesto al ángulo de 30 grados, trazó el lado de 8 centímetros.

 

El tercer estudiante primero trazó el lado de 8 centímetros, posteriormente el ángulo de 30 grados y, en el otro lado del ángulo, trazó el lado de 10 centímetros para terminar uniendo los extremos de los segmentos para completar el triángulo.

 

Si todos cumplieron con las tres medidas dadas, ¿por qué trazaron triángulos distintos? ¿Cuál de ellos cumple con la condición dada?

 

Si estás pensando que el error está en el orden de los trazos y la posición de las magnitudes, estás en lo correcto. Al momento de mencionar las medidas siempre hay que tomar en cuenta este orden dado para realizar los trazos, de lo contrario puedes trazar triángulos diferentes, como pudiste notar. Así que, de los estudiantes, quien siguió las instrucciones y construyó el triángulo correctamente fue el tercero, ya que cumplió con el orden dado; lado, ángulo y lado.

 

 

Es importante, que esta consideración la tengas muy presente, al momento de trazar un triángulo.

 

Ahora construirás cuadriláteros, siguiendo con el juego del telegrama. ¿Estás preparada o preparado? Toma lápiz y papel y registra los datos.

 

Telegrama:

Construir un rectángulo de 5 centímetros de base y 3 centímetros de altura. Y construir un rombo con lados de 4 cm y un ángulo de 150 grados.

 

¿Por qué en estos cuadriláteros sólo se dan 2 medidas? ¿Con ellas será posible construirlos?

 

Primero analiza las características del cuadrado y del rectángulo.

 

 

El cuadrado y el rectángulo son cuadriláteros conocidos como paralelogramos, ya que están formados por dos pares de lados paralelos.

 

El cuadrado tiene 4 lados iguales, el rectángulo tiene sus lados opuestos iguales y ambos tienen cuatro ángulos que miden 90 grados.

 

Sabiendo lo anterior y con la medida de sus lados, ya puedes construir el rectángulo.

 

Primero, trazas el lado de 5 centímetros, con apoyo del transportador trazas el ángulo de 90 grados en uno de sus extremos y sigues con la medida de 3 cm. Repites el proceso para completar el rectángulo.

 

Analiza ahora al rombo. ¿Cuál son sus características?

 

El rombo también es un paralelogramo, por tener un par de lados paralelos. Tiene sus 4 lados iguales, y sus ángulos opuestos son iguales, un par de ángulos son agudos y otro par, obtusos.

 

 

En el caso del rombo mencionado en el telegrama, sabes que sus lados serán de 4 cm y que sus ángulos obtusos miden 150 grados. Observa su construcción.

 

Trazas un segmento de 4 cm y, en uno de sus extremos, un ángulo de 150 grados; sobre la prolongación del lado del ángulo, mides un segmento de 4 centímetros. Ya tienes la mitad del rombo.

 

 

Para continuar, desde el extremo del segundo segmento de 4 cm, trazas una paralela al primer lado que trazas y pones una marca a los 4 cm. Finalmente, trazas el cuarto lado del rombo para cerrarlo.

 

 

Para saber la medida de los otros ángulos del rombo, aplicas la propiedad de los cuadriláteros que dice que la suma de sus ángulos interiores es de 360 grados.

 

 

La propiedad anterior ocurre porque, al cortar un cuadrilátero por una de sus diagonales, queda dividido en dos triángulos y, como la suma de los ángulos interiores de cualquier triángulo es de 180 grados; por consiguiente, en los cuadriláteros será de 180 grados + 180 grados igual a 360 grados.

 

En esta sesión estudiaste diversas situaciones con las que aprendiste a construir triángulos y cuadriláteros, a partir de conocer ciertas medidas y analizaste algunas de sus características.

 

Has terminado el tema del día de hoy.