ESPAÑOL - SECUNDARIA 1
Un gráfico dice un poco más que mil palabras
Te invitamos a realizar la siguiente actividad, para que te quede claro cómo usar en recurso gráfico.
Supongamos que nos interesa realizar una investigación sobre las maravillas del mundo moderno, y para ello queremos usar un mapa mental. Entonces, lo primero que haremos será recopilar la información relevante. Esto nos llevará a saber que las que se conocen como las maravillas del mundo moderno son siete.
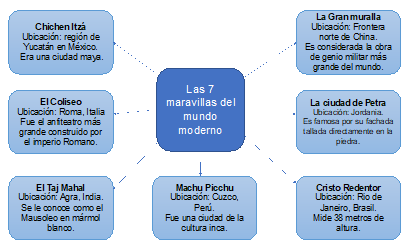
Las 7 maravillas del mundo moderno son:
Chichen Itzá, que se encuentra en la región de Yucatán, en México, y era habitada por la cultura Maya.
El Coliseo, ubicado en Roma, Italia fue el anfiteatro más grande construido por el imperio Romano.
El Taj Mahal, ubicado en Agra, en India, y conocido como el mausoleo en mármol blanco.
Machu Picchu, en Cuzco, Perú, fue una ciudad de la cultura inca.
La Gran Muralla, ubicada en la frontera norte de China, es considerada la obra de genio militar más grande del mundo.
La ciudad de Petra, ubicada en Jordania, es famosa por su fachada tallada directamente en la piedra.
Cristo Redentor, en Rio de Janeiro Brasil, que mide 38 metros de altura.
Ahora que tienes la información, puedes ya crear su mapa mental. Te puedes basar en el siguiente ejemplo. Usa tu imaginación y diséñalo e ilústralo como quieras.
Recuerda hacer uso de los recursos gráficos para apoyar tu investigación, que sean una manera sencilla y divertida de explicar toda la información que has recabado.
Para reforzar lo que has visto recapitulemos:
Los recursos gráficos ilustran o complementan la información de los textos, por ejemplo:
- Imágenes como: las fotografías, las ilustraciones o mapas.
- Organizadores textuales, como: los esquemas, cuadros sinópticos, mapas conceptuales y mentales.
- Las gráficas, diagramas y tablas.
La función de los recursos es presentar datos sintetizados en forma ordenada y clara. Esto facilita su lectura y la comprensión general del texto.
Un reto más, para que lo hagas en casa. Atención, te recomendamos escribir en tu libreta de anotaciones, para después elegir la respuesta correcta.
1. ¿Qué recurso gráfico ocuparían para su investigación, si desean ilustrar algo que nadie conoce?
a) Mapa conceptual
b) Imágenes e ilustraciones
c) Cuadro comparativo
2. Si tu investigación presenta datos variados y deseas compararlos entre ellos, ¿a qué elemento gráfico puedes recurrir?
a) Imágenes e ilustraciones
b) Mapa conceptual
c) Cuadro comparativo y gráficas.
3. Si deseo organizar la información en conceptos para que mi investigación sea más explícita ¿qué recursos gráficos puedo utilizar?
a) Imagen e ilustraciones
b) Mapa conceptual
c) Cuadro comparativo y gráficas
Seguramente pudiste identificar los recursos gráficos en cada caso. Te pedimos que investigues un tema de tu elección, para que a partir de éste elijas un recurso gráfico y lo integres a tu investigación.
Comencemos con unas preguntas para tu reflexión.

Estas preguntas te ayudan a reflexionar sobre la pertinencia de los recursos gráficos en tu investigación, si aportan algo al texto, o nada más están de adorno.
Durante tus investigaciones, obtendrás una gran cantidad de información. Los apoyos visuales pueden ayudarte a identificar y comparar la información que podría resultar confusa en un texto.
También la difusión de contenidos de la investigación es importante y, si quieres llamar la atención del lector, debes recurrir a varios recursos: las ilustraciones o gráficos pueden apoyarte para que el texto se comprenda mejor, y ayudará a tus lectores a absorber mejor el resultado de tu trabajo.
Por eso se suele decir que una imagen dice más que mil palabras, también, porque las imágenes ayudan a entender mejor el texto, pero también agregan un poco de información extra.
Por supuesto. Para hacer una investigación es importante considerar los recursos gráficos, pues ayudan a clarificar las ideas.
Una imagen puede decirnos de un solo golpe lo que abordaremos sobre un tema en un texto; es decir, es necesaria una relación estrecha entre el texto investigado y la imagen o gráfico. Así, la imagen y gráficos, con su capacidad ilustrativa, pueden ser clave para comprender el mensaje.
Pero entonces, ¿qué son los recursos gráficos?, ¿sólo son imágenes y fotografías?, ¿o hay otros recursos que nos sirven para organizar y profundizar nuestra investigación?
Los recursos gráficos ilustran o complementan la información de los textos, y los podemos clasificar de la siguiente manera:
1) Imágenes como fotografías, ilustraciones o mapas.
2) Organizadores textuales, como esquemas, cuadros sinópticos o mapas conceptuales y mentales.
3) También están las gráficas, diagramas y las tablas.
Todos estos recursos presentan datos sintetizados en forma ordenada y clara, a fin de facilitar su lectura y la comprensión de la información. Por ello debemos elegir la que más se adecue a lo que estamos investigando.

La investigación nos muestra información que el investigador quiere dar a conocer. Ello implica describir e interpretar su contenido.
Por ejemplo, si el texto habla sobre los viajes de Cristóbal Colón, será útil tener un mapa para que todos los lectores tengamos claro de qué rutas y partes del mundo estamos hablando.

A veces, la complejidad de un texto o el desconocimiento del vocabulario nos hacen creer que no entendimos lo que dice; sin embargo, cuando analizamos los gráficos e imágenes estos nos pueden apoyar y enriquecer nuestro conocimiento.
Por supuesto: hay una variedad de ordenadores textuales o gráficos que podemos usar, tales como:
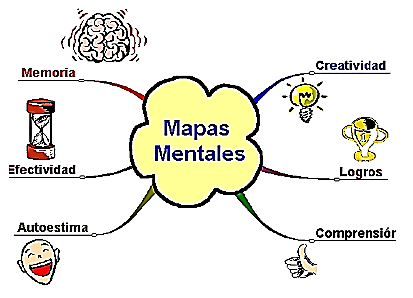
Mapa mental: asocia libremente conceptos e imágenes relativos al tema, usando formas como ramas o rayos para representar las relaciones entre ellas.
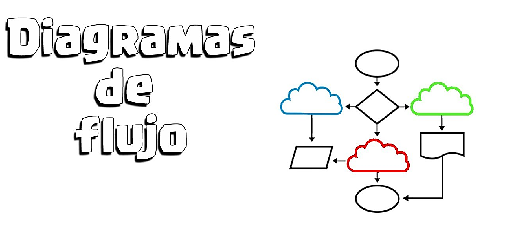
Diagrama de flujo: Presenta los pasos de un proceso o la secuencia de cambios en un fenómeno.
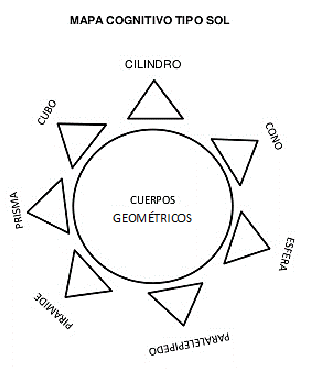
Mapa cognitivo tipo sol: es semejante a la figura de un sol. Sirve para introducir u organizar las ideas de un tema. En la parte central se anota el título o tema a tratar y en las líneas se anota los conceptos obtenidos sobre un tema.
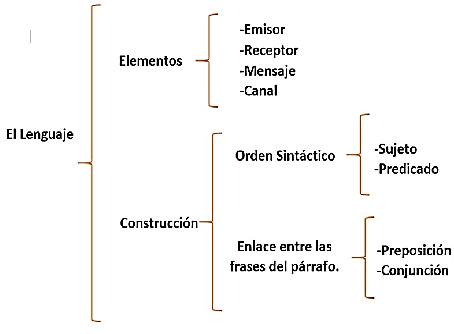
Cuadro sinóptico: resume y organiza, con llaves o corchetes la información de un tema de lo general a lo particular.
Existen otros recursos que nos ayudan a organizar nuestra investigación, pero estos son suficientes por ahora para comenzar a utilizarlos.
Existen varios recursos gráficos que podemos utilizar para presentar los resultados de nuestra investigación, y hacer que para nuestros lectores sea más comprensible lo que hemos indagado. Debemos seleccionar aquél que explique de mejor forma el texto que indagamos.
Las imágenes y gráficos nutren el contenido en la selección de fuentes de información, por eso debemos ser cautelosos al momento de elegirlos y clasificarlos, porque si no, podrían comunicar algo distinto de lo que queremos transmitir en nuestra investigación.
¿Cómo se realiza esta selección de gráficos e imágenes?
Es una elección que se lleva a cabo una vez que se tiene definido el tema de investigación. Sobre todo, se debe establecer una relación muy cercana entre la información y los gráficos, y debemos siempre tener en mente a qué tipo de lectores queremos presentarle nuestra información.
Por ejemplo:
Pensemos que el tema que hemos investigado es “el Sistema Circulatorio”, que básicamente depende del funcionamiento del corazón humano. Debemos pensar cómo manejar el tema para ser lo más claros posible.
Nuestro corazón presenta cuatro cámaras internas: de ellas, dos reciben sangre, las aurículas, y otras dos la expulsan, que son los ventrículos.
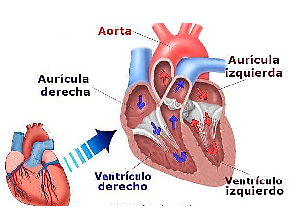
Entendamos que el corazón funciona como una bomba aspirante e impelente, es decir, que aspira y que expulsa. Para hacer esto, realiza movimientos de relajación (diástoles) seguidos de movimientos de contracción (sístoles). El ciclo cardíaco (lo que conocemos como latido) dura 0.8 segundos.
Si deseamos que sólo se conozca una imagen para señalar las partes del corazón y ubicar esto, se puede representar con una imagen que ilustre cómo se encuentra un corazón; sin embargo, si nuestra intención es tener presente el funcionamiento del corazón hay que recurrir a otro gráfico de índole textual, como el cuadro sinóptico.
Los dos tienen una finalidad: uno ilustra rápidamente la información y el otro profundiza en la explicación. Ahora bien, los dos se pueden plasmar para que sea clara nuestra investigación, de acuerdo con la intención con la que presentamos la investigación.
Cuando leemos y la información se apoya con gráficos, es más comprensible porque se relaciona la imagen con lo que está escrito.
Todas las imágenes son un apoyo visual. Por ejemplo, si decidimos investigar sobre Charles Darwin, autor de El origen de las especies, obra publicada en 1859, y queremos ilustrar los recorridos que hizo mientras estudiaba la evolución de las especies, nos será útil un mapa con la ruta.
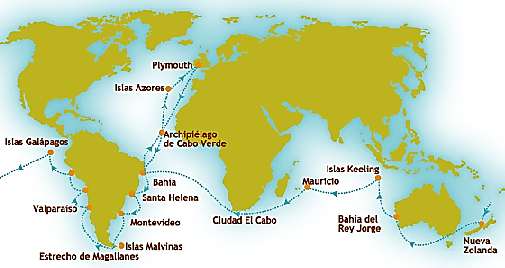
Pero también podemos apoyarnos con retratos del propio Darwin.

O esquemas como éste, que muestra visualmente la hipótesis sobre la evolución de las especies.

Es decir, elegiremos los recursos gráficos según lo que deseemos mostrar y ejemplificar con ellos.
Las gráficas nos pueden servir para ejemplificar esto, porque existen diversos tipos, como las de dispersión, las circulares, las de pastel y otras, y esto permite elegir la más adecuada para ilustrar el tipo de información que queremos presentar.
Con ellas se puede realizar un análisis de los resultados. Por ejemplo, el índice de natalidad o mortandad de la población en las décadas previas.
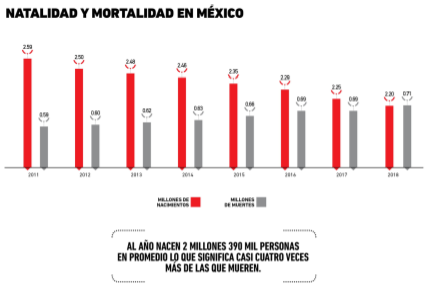
Quienes lean la investigación, podrán observar rápidamente el análisis de los datos recopilados. Los recursos son útiles siempre que se encuentren vinculados con el texto.
Otro recurso son las tablas comparativas o de datos. Por ejemplo, si nos interesa el tema del reino animal y deseamos comparar las diferencias entre vivíparos, ovíparos y ovovivíparos, podríamos ayudarnos con una tabla comparativa.
Vivíparos: son los animales que se forman en el vientre materno. Su nutrición es a través de la placenta, nacen cuando se encuentran completamente formados, y algunos ejemplos son el perro, la ballena o la vaca.
Ovíparos: son los animales que se forman dentro de un huevo, se nutren del contenido del huevo y cuando la cría ya está lista para nacer, rompe el cascarón. A esta categoría pertenecen animales como la hormiga, la gallina, el pingüino o el loro.
Ovovivíparos: son los animales que se forman dentro de un huevo que está dentro del vientre materno. Su nutrición fetal es a través de la placenta y también del contenido del huevo. Nacen cuando la cría cumple su proceso de desarrollo y la madre lo expulsa de su cuerpo. Por ejemplo, las mantarrayas, ornitorrinco o el sapo de Surinam.
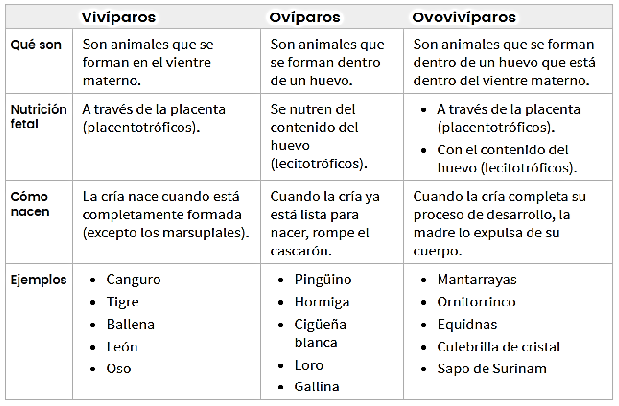
En este ejemplo vemos que un cuadro comparativo nos puede ayudar a comprender mejor las clasificaciones y descripciones de los vivíparos, ovíparos y ovovivíparos.
Después de la lectura de la investigación, podemos recurrir a este tipo de ordenadores gráficos, para facilitar la comprensión.
Después de hacer una lectura y una investigación, podemos apoyarnos de los mapas conceptuales, para organizar el tema de acuerdo con sus jerarquías y conceptos. Su lectura es sencilla y siempre están enlazados con conectores, que son palabras que articulan a los conceptos.
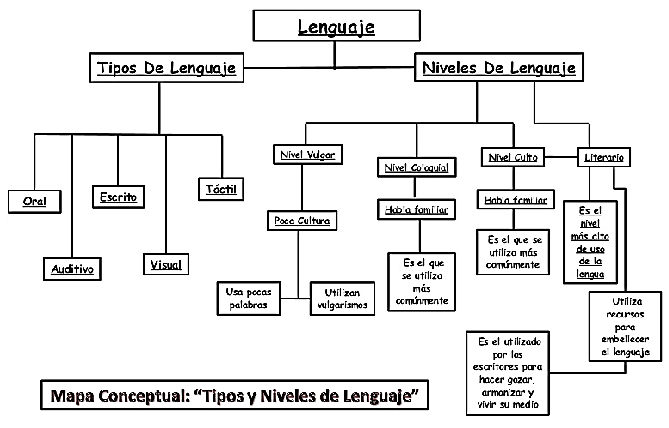
Los mapas conceptuales son distintos a los mapas mentales. Uno de los mapas plantea conceptos y el otro imágenes, pero siguen siendo recursos gráficos.
Observa el siguiente video del minuto: 00:28 a 04:32 para que conozcas este recurso, que es también considerado como un ordenador gráfico.
- Mapa de ideas o mapas conceptuales
https://www.youtube.com/watch?v=GMGZ9uW3PqA
El mapa mental sólo enuncia las partes de un tema, mientras que el conceptual las desarrolla en partes más pequeñas.