MATEMÁTICAS - SECUNDARIA 1
Alimentos proporcionales
El reto de esta sesión será que encuentres situaciones de la vida cotidiana, ejemplos en donde esté presente la variación proporcional. Analízalos, y si lo consideras útil, usa las tablas de variación de proporcionalidad directa.
Revisa el libro de texto de Matemáticas de Primer grado y resuelve los ejercicios que impliquen calcular valores faltantes en una tabla de variación.
Recuerda que en la sesión anterior analizaste que dos magnitudes guardan una relación de proporcionalidad directa, cuando al aumentar o disminuir una de ellas, la otra aumenta o disminuye en la misma proporción. Conforme a lo anterior, es importante, no perder de vista que una razón es la relación entre dos cantidades, que pueden ser de la misma naturaleza o no.
La razón entre a y b se denota de la siguiente forma, a.:b se lee “a” es a “b”. Por ejemplo:

Sabes o has aprendido que la proporción, es la igualdad de dos razones: a:b y c:d como: (a)(d) = (c)(b) por ejemplo:

Es por esta característica que se establece una relación de proporcionalidad directa entre las cantidades involucradas, ya que, al aumentar una cantidad, aumenta la otra en la misma proporción. Por lo anterior podríamos definir a la proporcionalidad directa como la relación que existe entre cuatro cantidades.
Para ejemplificar lo dicho anteriormente realicemos las siguientes actividades:
Era una mañana calurosa, y un grupo de amigos comentaba sobre las bebidas que los refrescaban más; dentro de las que mencionaron, estaban: refrescos, té helado, agua de frutas y algunas otras. En la reunión, una de las amigas que era nutrióloga les hablaba de los nutrientes de las bebidas, así como sobre la cantidad de azúcar que contenían las bebidas que les gustaba ingerir. Por ello, le preguntaron ¿Cuál es la cantidad diaria de azúcar que se recomendada? A lo que les respondió que.
La Organización Mundial de la Salud recomienda, en promedio, ingerir 1/40 de kilogramo, que son 25 gramos de azúcar para personas sin actividades físicas. Si se excede la cantidad recomendada, se podrían adquirir enfermedades tales como: diabetes, caries y obesidad.
Por lo tanto, los amigos empezaron a analizar las cantidades de azúcares que ingieren y verificar si existe una relación de proporcionalidad directa, ya que dependiendo de las bebidas y la cantidad que ingieren, es la cantidad de azúcares que obtienen de ese alimento.
Hay que hacer hincapié en que no debemos confundir la información nutrimental con el hecho de que el refresco sea nutritivo, ya que no aporta ningún nutriente a las personas. Revisando la información nutrimental de un refresco cuya presentación era de 500 mililitros, contiene 1/20 de kilogramo de azúcar. En esa semana uno de los amigos dijo haber consumido alrededor de 1 botella de 500 mililitros por día.
Para calcular la cantidad de azúcar que consumió en esa semana, observa el siguiente video hasta el minuto 03:20:
- Consumo de refresco
https://youtu.be/AWsf1ba2hWw
Para verificar si existe una relación de proporcionalidad directa entre las cantidades involucradas, podemos ayudarnos de una tabla de datos.
La tabla está formada por 2 columnas y 7 filas, en cada columna se han registrado las cantidades relacionadas a nuestra situación planteada. La primera cantidad corresponde a los mililitros consumidos de refresco y la segunda, refiere a los kilogramos de azúcar.
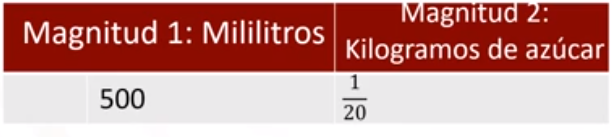
¿Qué cantidad de azúcar total se habrá consumido para el segundo día?
En la segunda fila se registra la cantidad del primer día por 2, esto es debido a que para el segundo día, ya se ha consumió el doble de refresco que el primer día, junto con la cantidad de azúcar que es el doble de la cantidad que el primer día.
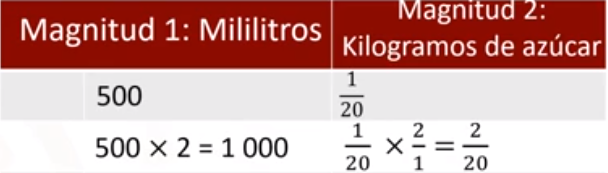
¿Qué cantidad de azúcar se consumió en total el tercer día?
Se registra en la fila 3 la cantidad de refresco que se consume ese día, 500 ml por 3, junto con la cantidad de azúcar que se ingirió, para ello multiplicamos 1/20 por 3 que es igual a 3/20.
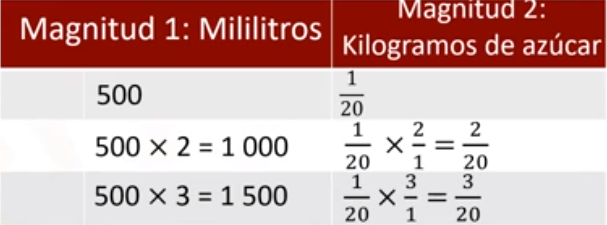
¿Cuál es la cantidad de azúcar total que se consume en el cuarto día? Nuevamente multiplicamos la cantidad de refresco que es 500 ml por 4, y la cantidad de azúcar se multiplica por 4, es decir: 1/20 por 4 que es igual a 4/20.
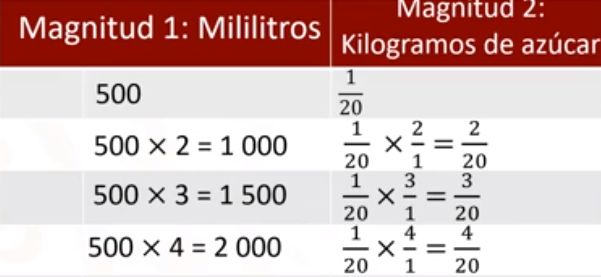
¿Qué cantidad de azúcar se consume en el quinto día?
Se continúa multiplicando la cantidad de refresco que es 500 ml por 5, cuyo producto es 2500, después la cantidad de azúcar por 5, que es, 1/20 por 5, es igual a 5/20.

¿Qué cantidad de azúcar se consumió para el sexto día? Se multiplica 500 por 6 que es igual a 3000, es decir, se consumen 3000 mililitros de refresco; y para calcular su correspondiente en azúcar se multiplica 1/20 por 6, que es igual a 6/20 de kilogramo de azúcar.

Finalmente se multiplica 500 por 7, cuyo producto representa 3500 mililitros de refresco y 1/20 por 7 que es igual a 7/20 de kilogramo de azúcar. Encontramos que se consumió 3500 mililitros de refresco, mismos que contienen 7/20 de kilogramo de azúcar.

¿Cómo sabemos que los datos son los correctos? Para verificarlo, observa el siguiente video del minuto: 03:21 al 05:35
- Consumo de refresco
https://youtu.be/AWsf1ba2hWw
Observamos que en la primera columna se ha registrado la cantidad en mililitros de refresco que se consume por día, asimismo en la segunda columna se ha registrado la cantidad de kilogramos de azúcar que se consume en correspondencia con los días registrados. Sabemos que en el día 1 se consumen 500 mililitros de refresco y esto aporta 1/20 kilogramos de azúcar al organismo.
Si para el día 2 se ha consumido el doble de la cantidad en mililitros de refresco que se consume el día anterior, se duplica la cantidad en mililitros de refresco y asimismo se duplica la cantidad en kilogramos de consumo de azúcar.
Si en el día 3 se consume el triple de la cantidad en mililitros de refresco que se consume el día 1, se triplica la cantidad en mililitros de refresco y asimismo se triplica la cantidad en kilogramos de consumo de azúcar.
Si en el día 4 se consume el cuádruple de la cantidad en mililitros de refresco que se consume el día 1, se cuadruplica la cantidad en mililitros de refresco y asimismo se cuadruplica la cantidad en kilogramos de consumo de azúcar.
Si en el día 5 se consume el quíntuple de la cantidad en mililitros de refresco que se consume el día 1, se quintuplica la cantidad en mililitros de refresco y asimismo se quintuplica la cantidad en kilogramos de consumo de azúcar.
Si en el día 6 se consume el séxtuple de la cantidad en mililitros de refresco que se consume el día 1, se sextuplica la cantidad en mililitros de refresco y asimismo se sextuplica la cantidad en kilogramos de consumo de azúcar.
Si en el día 7 se consume el séptuple o 7 veces la cantidad en mililitros de refresco que se consume el día 1, se septuplica la cantidad en mililitros de refresco y asimismo se septuplica la cantidad en kilogramos de consumo de azúcar.
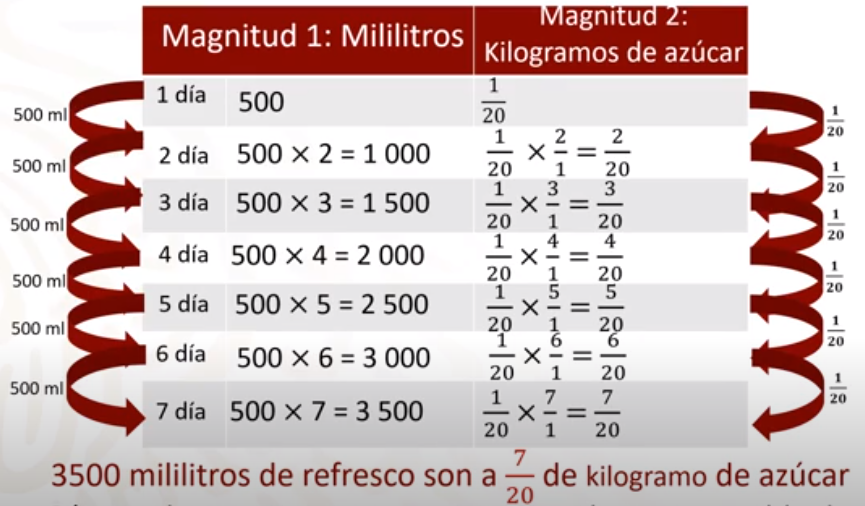
Como identificaste, las cantidades relacionadas entre sí aumentan en la misma proporción, por lo que se puede concluir que están en una relación directamente proporcional.
Analizando la relación entre la cantidad de azúcar que contiene el refresco, y la cantidad de azúcar que provee su consumo, ¿se consumió lo recomendado por la OMS?, ¿qué piensas?
En esa misma semana de lunes a viernes, esa persona había consumido 2500 mililitros de té helado. Si cada 500 mililitros contienen 1/35 de kilogramo de azúcar, ¿cuál es la cantidad de azúcar que habría consumido en esa semana?
Para analizar el procedimiento y responder la pregunta, observa el siguiente video:
- Consumo de té
https://www.youtube.com/watch?v=OqXwBZ9cTrY
Para apoyar nuestro análisis es conveniente construir una tabla de variación. En la primera columna colocamos el té helado que se ha consumido durante toda la semana, y del otro lado los kilogramos de azúcar que contienen 500 ml de té helado. del lado de las filas son los días de la semana que van del lunes al viernes.
Sabemos que el día 1 se ha consumido 500 ml de té y esto aporta 1/35 de kilogramo de azúcar al organismo.
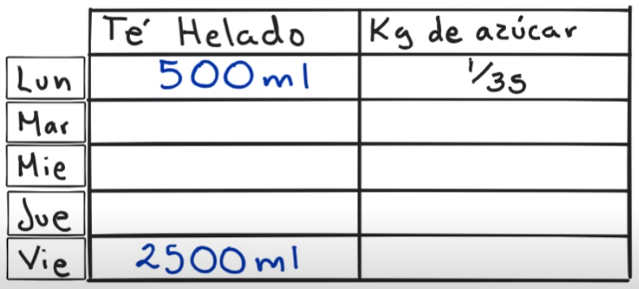
Si para el día 2 se ha consumido el doble de la cantidad en mililitro de té que se consume el día anterior, se duplica la cantidad en mililitros de té, así que serán 1000 mililitros.

Si en el día 3 se consume el triple de la cantidad en mililitros de té que se consume en el día 1, se triplica la cantidad en mililitros de té, por lo tanto, son 1500 mililitros.

Para el día 4 se consume el cuádruple de la cantidad en mililitros de té que se consume el día 1, se cuadruplica la cantidad en mililitros de té, así que ya serán 2000 mililitros.

Para el día 5 se habrá consumido el quíntuple de la cantidad en mililitros respecto al día 1, que son 2500 mililitros.

Para resolver la segunda columna, tenemos la siguiente proporción: por cada 500 ml de té helado, se consume 1/35 de kg de azúcar.
Para el día 2 se ha consumido el doble de la cantidad en kilogramos de azúcar que se consume el día anterior, se duplica la cantidad en kilogramos de azúcar, así que multiplico por 2; convertimos en fracción el 2 y multiplicamos de forma directa; dos por una dos y treintaicinco por 1, treintaicinco. Esto da 2 treintaicincoavos.
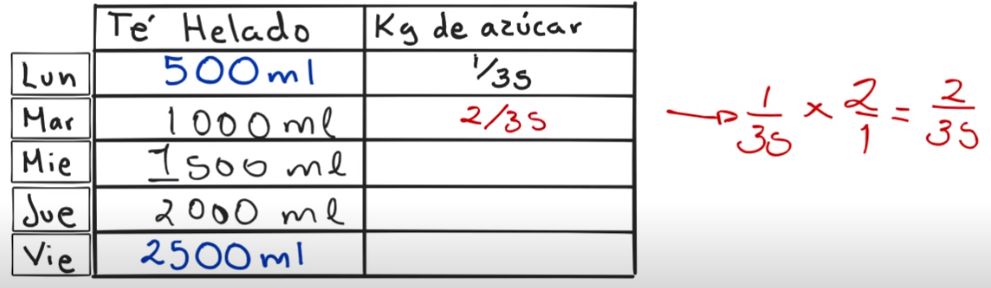
Para el día 3, se triplica la cantidad de azúcar en kilogramo que se consume el día 1, por lo que multiplicamos 1/35 por 3; lo convertimos en fracción y multiplicamos directo, 3 por 1, 3; y 35 por 1, 35; 3 treintaicincoavos de kilogramo.

Puedes darte cuenta que hay una relación entre cada fracción. Observa, para el día lunes es 1 treintaicincoavo, para el día martes, 2 treintaicincoavos; para el día miércoles 3 treintaicincoavos; ¿qué seguiría?
El jueves serían 4 treintaicincoavos, ya que se cuadruplica la cantidad de azúcar en kilogramos y el viernes 5 treintaicincoavos de kilogramo de azúcar, por lo tanto, se quintuplica la cantidad de azúcar.
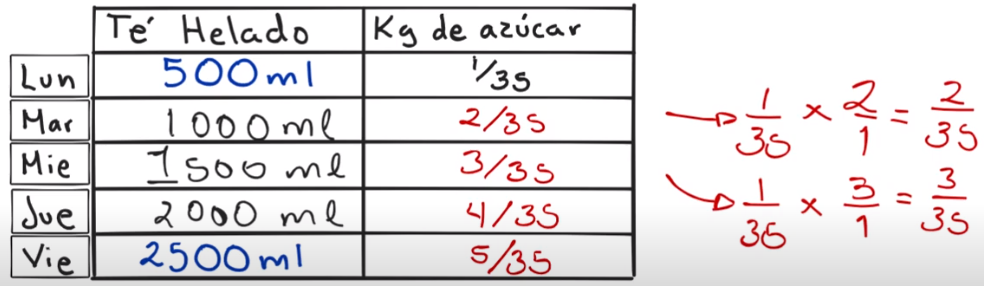
En una relación de proporcionalidad directa al multiplicar los datos del segundo conjunto por la constante de proporcionalidad, la cual se representa convencionalmente con la letra k, se obtienen los datos correspondientes del primer conjunto y viceversa, multiplicando por el inverso multiplicativo de esa constante.
Veamos otro ejemplo: En una casa preparan una jarra de 2 litros de agua de jamaica, cuya preparación utiliza 1/6 de kilogramo de azúcar ¿qué cantidad de azúcar se necesitaría para preparar 1 litro y 3 litros de agua?, ¿qué procedimiento utilizarías para obtener una menor porción de agua? En este caso vamos a utilizar una propiedad de los números llamada, inverso multiplicativo.
- JARRA DE AGUA
https://youtu.be/0pLRz2kOfMs
Se llama inverso multiplicativo de un número, a aquel número que, al ser multiplicado con el número original, es decir, con a; da como resultado 1.
El inverso multiplicativo de un número racional a entre b, siempre será b entre a, es decir, ahora el numerador del número original será denominador y el denominador, numerador; y esto se cumple para todos a y b, que sean distintos de cero.
Revisemos unos ejemplos, el inverso multiplicativo de tres séptimos (3/7) es siete tercios (7/3). ¿Cómo lo comprobamos? Tenemos que tres séptimos (3/7) por siete tercios (7/3) es igual a veintiún veintiunavos (21/21), recuerda que cuando tenemos el mismo numerador y denominador, esto es igual a uno.
Otro ejemplo, el inverso multiplicativo de dos quintos (2/5) es cinco medios (5/2), comprobamos, dos quintos (2/5) por cinco medios (5/2) es igual a 2 x 5 = 10, 5 x 2 = 10, es igual a diez décimos (10/10), y esto es 1; por lo tanto, se cumple la propiedad del inverso multiplicativo, donde al multiplicar ambos números, resulta 1.
¿Cómo aplicamos el inverso multiplicativo en una división de fracciones? Revisémoslo por medio de este ejemplo:
Un medio (1/2) entre tres quintos (3/5), lo primero que tenemos que hacer es ubicar el divisor, ¿Quién es el divisor?, tres quintos (3/5), por lo que aplicaremos el inverso multiplicativo de éste, que es cinco tercios (5/3); ahora sabemos que un medio (1/2) entre tres quintos (3/5) es igual que multiplicar un medio (1/2) por el inverso multiplicativo del divisor, que es cinco tercios (5/3); y esto es igual 1 x 5 = 5 y 2 x 3 = 6; así que el resultado de la división es cinco sextos (5/6).
Para resolver la situación anterior utilizaremos las tablas de variación, observa el siguiente video del minuto: 3:00 al 5:35 para resolverlo.
- JARRA DE AGUA
https://youtu.be/0pLRz2kOfMs
Para resolver dicha situación nos apoyaremos de una tabla en donde las cantidades que se relacionan son los litros de agua y los kilogramos de azúcar. La situación menciona que para preparar dos litros de agua se requiere de un sexto de kilogramo de azúcar; ¿Qué cantidad utilizaremos para uno y tres litros de agua?, ¿Qué operación podemos realizar?

Podemos dividir un sexto, que es la cantidad de azúcar que se utiliza para preparar dos litros de agua de jamaica, entre dos y así conocer lo que se utilizaría para preparar un litro de agua de jamaica, convertimos nuestro entero a fracción, colocando como denominador al número uno. Para ello, aplicaremos el inverso multiplicativo, ¿Quién es el divisor?, dos enteros y su inverso multiplicativo es un medio. Entonces, un sexto entre dos enteros tiene el mismo resultado que multiplicar un sexto por un medio, esto es igual a uno por uno, uno; seis por dos, doce; un doceavo; por lo tanto, para preparar un litro de agua se requiere de un doceavo de kilogramo de azúcar.
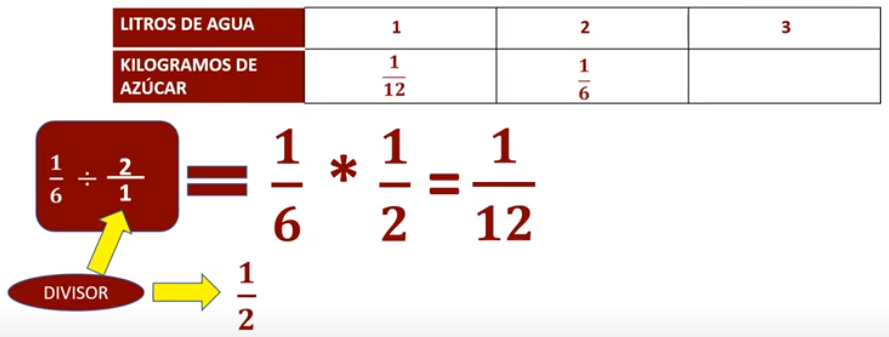
Como ya tenemos el valor unitario es más práctico calcular el azúcar presente en tres litros de agua. ¿Qué haremos?
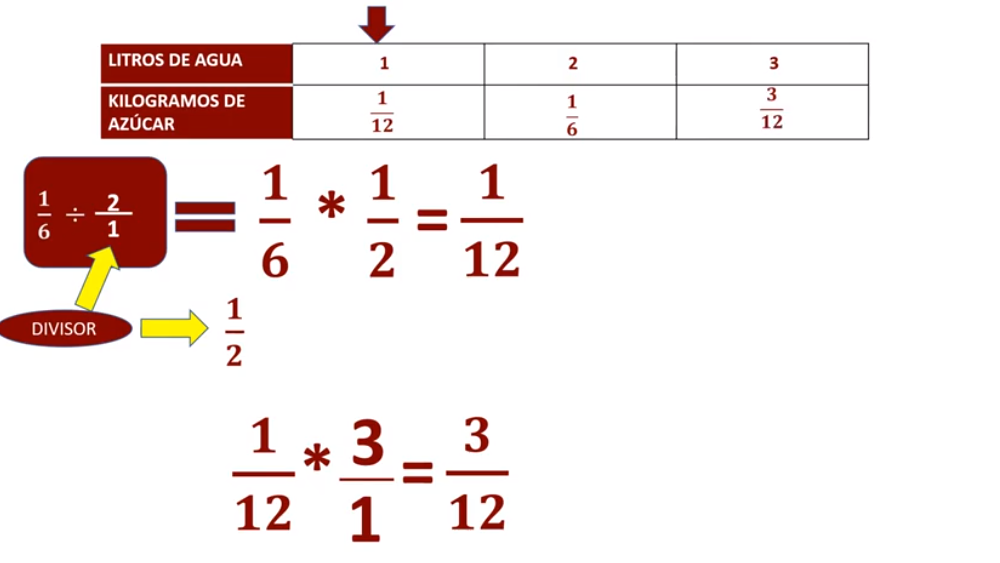
Multiplicamos un doceavo, que es la cantidad de azúcar que se necesita para preparar un litro de agua, por tres, que es la cantidad de litros de agua que deseamos preparar, convertimos nuestro entero a fracción y esto es igual a uno por tres, tres; doce por uno, doce; tres doceavos, por lo tanto, para preparar tres litros de agua se requieren tres doceavos de kilogramo de azúcar.
¿Has preparado en casa chocolate caliente? Una olla para cuatro porciones utiliza en promedio 3/10 de kilogramo de azúcar. ¿Qué cantidad de azúcar se utilizará para una, dos, tres y cinco porciones?
- La OLLA
https://youtu.be/w9XrY-zgC7c
Para dar respuesta a nuestra situación usaremos una tabla como las anteriores, en la primera columna registraremos las porciones que se necesitan elaborar y en la segunda, los kilogramos de azúcar que se requieren por porción.

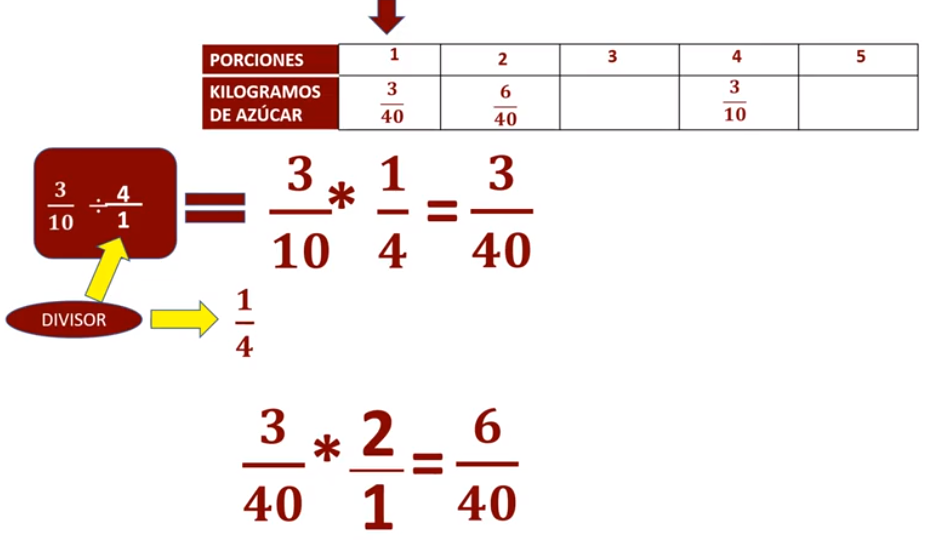
La situación planteada, menciona que para cuatro porciones se requieren tres décimos de kilogramo de azúcar. ¿Cuál es la cantidad de azúcar que utilizaremos para una, dos, tres y cinco porciones? Dividiremos tres décimos, que es la cantidad de azúcar para cuatro porciones entre cuatro; y así conocer la cantidad de azúcar para una porción. Convertimos el entero a fracción colocando al número uno como denominador; para ello utilizaremos el inverso multiplicativo. En esta operación ¿Cuál es el divisor? 4 enteros y su recíproco es un cuarto; por lo tanto, el cociente de tres décimos entre cuatro enteros es el mismo que el producto de tres décimos por un cuarto.

Por lo tanto, para una porción de chocolate caliente se requieren tres cuarentavos de kilogramo de azúcar.
¿Y para dos porciones? Como ya tenemos el valor unitario, podemos multiplicar tres cuarentavos por dos, convertimos nuestro entero a fracción, y resolvemos tres por dos, seis; cuarenta por uno, cuarenta seis cuarentavos; para dos porciones se requieren seis cuarentavos de kilogramos de azúcar.
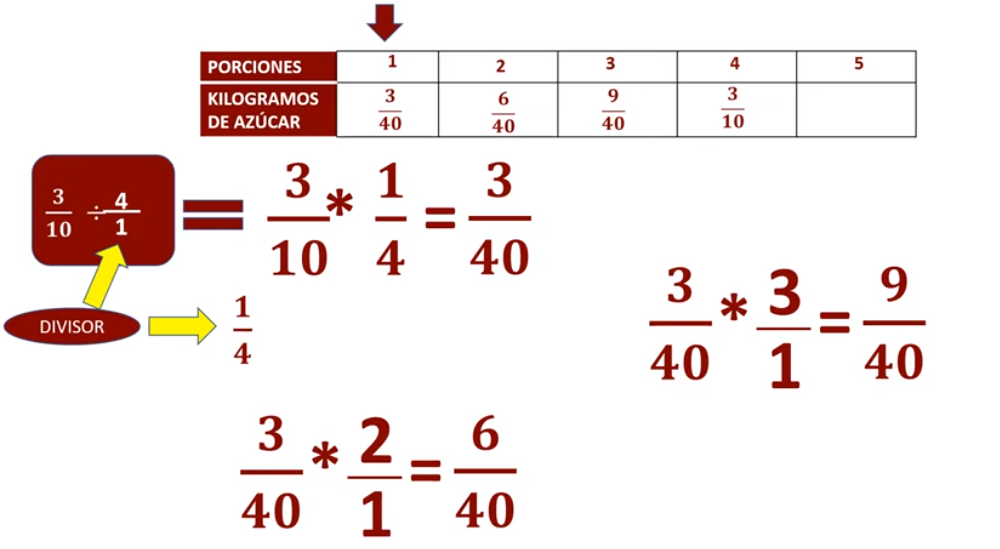
Y, ¿para tres porciones? Multiplicamos tres cuarentavos por tres, convertimos nuestro entero a fracción y obtenemos tres por tres, nueve, cuarenta por uno, cuarenta; nueve cuarentavos, para tres porciones se requieren tres cuarentavos de kilogramo de azúcar y para cinco, quince cuarentavos.
Es muy importante limitar nuestro consumo de azúcar para llevar una vida más saludable, si es que nuestro consumo no es el adecuado.
Tal vez enfrentaste dificultades para encontrar el inverso multiplicativo de un número entero. Una de las posibles causas es que hayas omitido el paso de convertir el número entero a fracción, colocando en el denominador un 1, recuerda que se le coloca el número uno, ya que no altera el valor numérico de dicho número, sólo es otra forma de escribirlo; para –posteriormente- encontrar su inverso multiplicativo, en el cual el numerador pasa a ser denominador y el denominador, numerador.






