GEOGRAFÍA - SECUNDARIA 1
Los conflictos territoriales en México
(VIERNES 19 MARZO)
ACTIVIDAD:
Investiga y elige algún conflicto territorial de tu localidad o entidad, y elabora una ficha técnica del caso, anotando dónde se localiza el conflicto, la causa, quiénes intervienen en él, las consecuencias; y si éste ya se solucionó, y ¿cómo se solucionó?
Piensa, ¿qué otro dato podrías agregar a tu ficha? Podrías agregar alguna ilustración o un mapa.
RESUMEN:
¿Has escuchado algo al respecto del caso de los Chimalapas?
¿Cómo es que se pueden derivar problemas, entre dos partes, al interior del país?
¿Te has confrontado con alguien de tu familia porque usa alguno de tus artículos preferidos?
¿Qué ocurrió para que esta situación terminara?
Pues algo similar, pero a mayor escala, ocurre en los conflictos territoriales, en donde el enfrentamiento se deriva por la propiedad o aprovechamiento de un territorio.
Y no necesariamente es un país extranjero el que llega a reclamar la propiedad de dicho territorio.
Sin duda cada metro cuadrado del planeta tiene un valor incalculable, pero sabiendo que cada espacio geográfico es único y diverso, seguro habrá algunos, que desde cierta perspectiva, pueden llegar a tener más valor.
Un conflicto territorial es la presencia de un desacuerdo entre dos o más partes sobre la pertenencia de un territorio o parte de él.
Este tipo de desacuerdos ocurren entre países, entre estados de un mismo país y entre localidades o municipios.
Generalmente, esta diferencia se debe a la situación estratégica de dicho territorio o a la presencia de algún recurso natural de gran valor.
Es decir que, ¿el componente natural de ese espacio geográfico se ve acechado por varias partes interesadas?
Así es, en México se presentan varios conflictos territoriales.
Entre sus causas están: las divisiones territoriales no bien definidas entre dos o más entidades federativas, como las 25, 000 hectáreas que disputan Nayarit y Jalisco; o entre dos o más municipios de una misma entidad, como en el caso de las tierras que pelean los municipios de Capulhuac y Ocoyoacac del Estado de México; la creación de municipios sin estudios históricos y demográficos, sin decretos que lo fundamenten, como la fundación del municipio Calakmul de Campeche, que afectó los territorios de Quintana Roo y Yucatán; la arbitrariedad de particulares y empresas privadas que invaden zonas para provechar sus recursos naturales, como en Cherán, Michoacán; y la invasión de tierras tanto en zonas rurales como urbanas por campesinos o grupos vulnerables, algunas veces apoyados por grupos políticos, como en los alrededores de las áreas de reserva de la Sierra de Guadalupe, en el Estado de México.
Analiza un conflicto territorial que tiene lugar en el sureste mexicano.
Este conflicto se desarrolla entre los estados de Oaxaca y Chiapas por la posesión de una región de gran riqueza natural, hablamos de la región de los Chimalapas.
En el sureste mexicano, es en donde predominan las regiones de selva y bosque en el país, regiones que cuentan con un alto grado de biodiversidad.
La región de los Chimalapas se encuentra en el corazón del Istmo de Tehuantepec, en el oriente del estado de Oaxaca; y se destaca por ser el lugar cuyas selvas húmedas y bosques mesófilos se encuentran en muy buen estado de conservación, por lo que es la zona de mayor biodiversidad de México.
Incluso, en el año 2014, se estimó que dicha región produjo 40% de los escurrimientos pluviales del país, es decir que esta área de 595, 000 hectáreas fue responsable de producir casi la mitad de los escurrimientos pluviales en el territorio nacional.
Además, en esta región nacen los ríos Coatzacoalcos, Uxpanapa y Tonalá.
Chimalapas, en náhuatl significa: "agua de los escudos", y en lengua zoque quiere decir: "jícara de oro".
Sin duda estos nombres hacen referencia a su gran riqueza natural.
Ahora, para que conozcas acerca de esa riqueza natural de los Chimalapas, te invito a ver y escuchar el siguiente audiovisual. Observa del minuto 00:08 al 04:05.
- Chimalapas, Una ventana a las selvas húmedas.
https://www.youtube.com/watch?v=4cNPpZEPLGw
Cómo pudiste identificar en el audiovisual la región cuenta con una gran diversidad de flora y fauna.
La combinación de la selva húmeda y el bosque, propician que su biodiversidad sea abundante.
Si bien están presentes los dos tipos de regiones es común que, sólo se le llame la selva de los Chimalapas.
En esta región, la selva de los Chimalapas, están asentadas dos comunidades agrarias: Santa María y San Miguel; y son propiedad del pueblo indígena zoque chimalapa, descendiente de los olmecas.
Ambas comunidades están registradas desde la colonia como parte del territorio de Oaxaca.
Ya que los zoques oaxaqueños cuentan con un título de propiedad que confirma que la corona española les vendió sus tierras, 900 mil hectáreas de Santa María, por 25 mil pesos oro.
¿Cómo fue que se produjo el conflicto por las tierras en los Chimalapas?
Un primer incidente ocurrió en la década de 1940.
Cuando se estableció en la región una empresa maderera, de origen michoacano, que obtuvo concesiones para explotar los recursos forestales en las tierras comunales de los zoques de Santa María y San Miguel Chimalapa.
Eso debió ser una gran afrenta por el saqueo de sus tierras.
Pero, ¿cuándo comenzó el conflicto entre los estados vecinos: Oaxaca y Chiapas?
El conflicto por la selva de los Chimalapas comenzó en 1967 fecha en la que el gobierno federal concedió al estado de Chiapas 6, 000 hectáreas de esta región, localizadas en territorio oaxaqueño, y a la que llegaron asentamientos de tzotziles y zoques chiapanecos; lo que inconformó a los zoques oaxaqueños, y desde ese entonces la disputa persiste.
¿Te das cuenta de cuáles son las partes involucradas en este conflicto?
Se logra identificar a los pobladores, al gobierno federal que otorgó las tierras y a los gobiernos locales que entraron en disputa por la posesión de éstas.
Exacto, pero además que entre los pobladores están: la población originaria, zoques oaxaqueños; y por otro lado los pobladores que llegaron, los zoques y los tzotziles procedentes de Chiapas.
El conflicto se remonta a la concesión de estas tierras al pueblo y gobierno chiapaneco.
Aunque desde antes venían ocurriendo irregularidades como la entrada de empresas madereras, que se comentaron; y, posteriormente, se han ido sumando más y más acontecimientos que han vuelto más y más complejo el problema.
¿Y cuál fue la reacción del pueblo oaxaqueño zoque?
El pueblo oaxaqueño zoque lleva décadas protestando por la explotación de los recursos de la región, que involucra la deforestación y la tala indiscriminada de la selva debido a la sobreexplotación de dos recursos de gran valor: la caoba y el cedro.
La disputa por la posesión del territorio y el uso de los recursos de esta región, ha tenido como consecuencia enfrentamientos violentos entre oaxaqueños y chiapanecos. Por ejemplo, los zoques, oaxaqueños y dueños originarios de esas tierras llegaron a quemar algunos asentamientos chiapanecos por considerarlos invasores de sus tierras
Además, se han favorecido desacuerdos políticos entre los gobiernos de los estados.
Una consecuencia más, es la explotación desmedida de la selva y el bosque, la deforestación, y con ello la consecuente pérdida de biodiversidad.
¿Qué otro tipo de acciones tomaba la población que se sentía despojada de su tierra?
Cerraban los caminos para que no pasaran a la selva o al bosque los camiones de los taladores; o bien confiscaban los camiones que salían de la zona repletos de madera y otros productos forestales.
Defendían su territorio y sus recursos a toda costa y esto explica porque eran y son tierras comunales.
El término tierras comunales, se refiere a que de manera institucional una superficie de terreno se ha concedido como propiedad a un grupo de personas determinado; en este caso, a los zoques, lo que incluye las tierras, agua, bosques y otros recursos naturales.
Una variable más -que complicó el conflicto- fue que en el año 2008 se otorgaron alrededor de 7, 000 hectáreas de la comunidad de San Miguel, a una empresa canadiense para su exploración y explotación minera, cuya concesión tendría una duración de 50 años, por lo que culminaría hasta el 2058.
¿Y cuáles eran los intereses de la empresa minera?
Su propósito era extraer minerales como el oro, la plata y el cobre.
Esto desencadenó la oposición de los habitantes de las comunidades de Oaxaca, así como diversos grupos ambientalistas.
Lo destacable de esta situación es que se unieron todos los comuneros, es decir los comuneros zoques y los tzotziles pues ante el acecho de las empresas privadas unieron fuerzas para oponerse a la explotación de sus tierras y sus recursos.
Juntos protestaron y denunciaron la presencia de un enemigo común que atentaba contra los recursos de sus tierras.
Y de la conservación de la región, ya que es común que la extracción mineral conlleve la alteración de la vegetación natural, la contaminación de los cuerpos de agua del lugar y la contaminación del aire.
¿Y sí se instaló la mina?, ¿continúa operando?
No, ante la movilización de los habitantes de la región y la búsqueda incesante del diálogo con las autoridades, a fines del año pasado los gobiernos federal, estatal y local acordaron cancelar el proyecto minero y propusieron impulsar un proyecto ecoturístico en la región.
Se observan dos caminos para resolver el conflicto, ya que hubo momentos en los que se presentaron soluciones violentas y posteriormente se buscó la solución pacífica, a través del diálogo; pero supongo que siempre manteniéndose firmes y exigiendo sus derechos.
De hecho, el conflicto no se ha resuelto del todo, esto último -de la denuncia y rechazo a que se instalara la empresa minera y su resolución institucional-, sólo es una solución a una parte del conflicto.
¿Qué parte del conflicto aún persiste?
La lucha contra las empresas madereras por la explotación legal e ilegal de la selva y el bosque.
¿Cómo se pueden ordenar las ideas para hacer una síntesis de este conflicto?
Observa cómo elaborar un organizador gráfico en el que sintetizas las variables que componen la problemática.
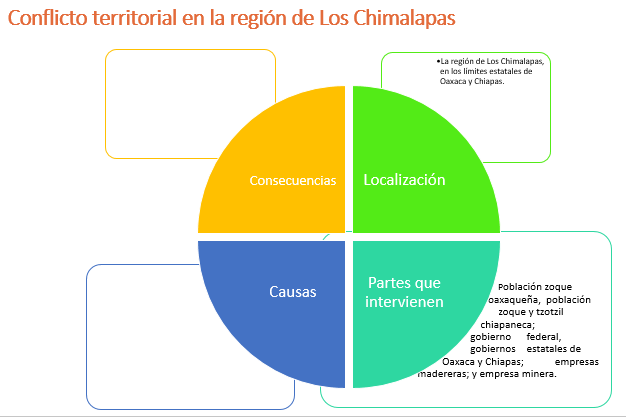
Las variables que intervienen en el conflicto, para su análisis: su localización, las partes que intervienen; la causa o causas del conflicto; y las consecuencias.
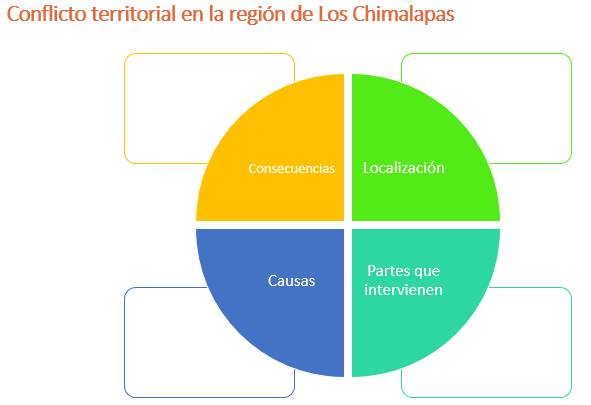
Se comienza por señalar: en dónde se localiza el conflicto del que se ha estado hablando.
La zona en conflicto es la región de Los Chimalapas, en los límites estatales de Oaxaca y Chiapas. Ahora identifica las partes que intervienen en el conflicto.
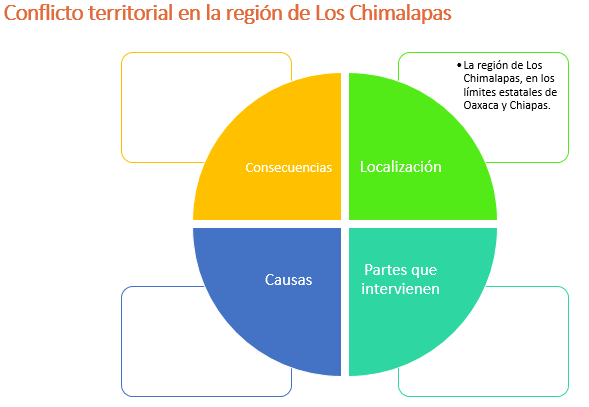
Interviene la población que ahí se asienta, originalmente los dueños de esas tierras; los zoques oaxaqueños; también la población que llegó a habitar las tierras los zoques y tzotziles chiapanecos; están además el gobierno federal -que cedió las tierras-, los gobiernos estatales de Oaxaca y Chiapas; las empresas madereras; y, anotemos también, la empresa minera que sabemos que estuvo interesada en la región, aunque por el momento detuvieron su proyecto.
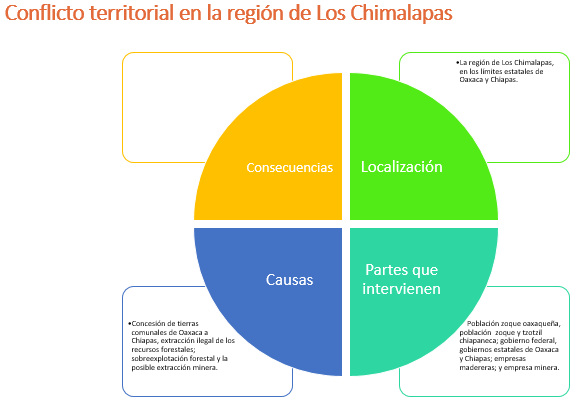
Continúa con las causas que propiciaron el conflicto:
La concesión de tierras comunales de Oaxaca a Chiapas, la extracción ilegal de los recursos forestales; la sobreexplotación forestal y la posible extracción minera.
El enfrentamiento entre pueblos hermanos, zoques oaxaqueños y tzotziles y zoques chiapanecos; la quema de casas; enfrentamientos violentos con las empresas madereras, bloqueo de caminos, decomiso de camiones, con el saqueo de los recursos de la región; explotación excesiva de la selva y el bosque, deforestación y pérdida de biodiversidad.
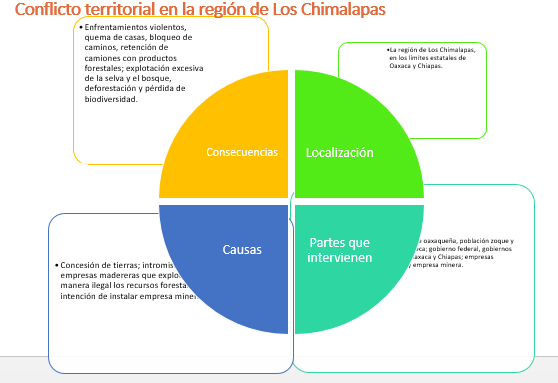
Agrega recortes o dibujos para que sea un trabajo más completo.
El análisis de este tipo de conflictos, desde la perspectiva de la Geografía, deja ver el entramado de los componentes del espacio geográfico.
Por un lado, se tiene un lugar: los Chimalapas, ubicado en una región con gran riqueza de flora y fauna; además de yacimientos minerales; esto corresponde al componente natural.
¿Qué otro componente identificas en el conflicto?
Podría ser el componente social representado por los habitantes originales de la zona; y los nuevos pobladores que arribaron cuando les cedieron parte de esas tierras.
También interviene el componente político representado por la intervención de los gobiernos federal, estatal y local; así como el activismo de los comuneros y campesinos.
Igualmente está presente el componente económico, constituido por las negociaciones monetarias motivadas por las empresas.
Recuerda las preguntas que se plantearon al inicio, reflexiona en ellas y respóndelas.
Considera que puedes seguir investigando más sobre el tema de los conflictos territoriales en tu libro de texto.
Si quieres saber más acerca de esta región de los Chimalapas y su problemática, pueden ver la entrevista realizada a una habitante y activista de esa zona en el video "Guardianes de los Chimalapas", Revista de la Universidad; lo pueden encontrar en la página:
Investiga y elige algún conflicto territorial de tu localidad o entidad, y elabora una ficha técnica del caso, anotando dónde se localiza el conflicto, la causa, quiénes intervienen en él, las consecuencias; y si éste ya se solucionó, y ¿cómo se solucionó?
Piensa, ¿qué otro dato podrías agregar a tu ficha? Podrías agregar alguna ilustración o un mapa.
¿Has escuchado algo al respecto del caso de los Chimalapas?
¿Cómo es que se pueden derivar problemas, entre dos partes, al interior del país?
¿Te has confrontado con alguien de tu familia porque usa alguno de tus artículos preferidos?
¿Qué ocurrió para que esta situación terminara?
Pues algo similar, pero a mayor escala, ocurre en los conflictos territoriales, en donde el enfrentamiento se deriva por la propiedad o aprovechamiento de un territorio.
Y no necesariamente es un país extranjero el que llega a reclamar la propiedad de dicho territorio.
Sin duda cada metro cuadrado del planeta tiene un valor incalculable, pero sabiendo que cada espacio geográfico es único y diverso, seguro habrá algunos, que desde cierta perspectiva, pueden llegar a tener más valor.
Un conflicto territorial es la presencia de un desacuerdo entre dos o más partes sobre la pertenencia de un territorio o parte de él.
Este tipo de desacuerdos ocurren entre países, entre estados de un mismo país y entre localidades o municipios.
Generalmente, esta diferencia se debe a la situación estratégica de dicho territorio o a la presencia de algún recurso natural de gran valor.
Es decir que, ¿el componente natural de ese espacio geográfico se ve acechado por varias partes interesadas?
Así es, en México se presentan varios conflictos territoriales.
Entre sus causas están: las divisiones territoriales no bien definidas entre dos o más entidades federativas, como las 25, 000 hectáreas que disputan Nayarit y Jalisco; o entre dos o más municipios de una misma entidad, como en el caso de las tierras que pelean los municipios de Capulhuac y Ocoyoacac del Estado de México; la creación de municipios sin estudios históricos y demográficos, sin decretos que lo fundamenten, como la fundación del municipio Calakmul de Campeche, que afectó los territorios de Quintana Roo y Yucatán; la arbitrariedad de particulares y empresas privadas que invaden zonas para provechar sus recursos naturales, como en Cherán, Michoacán; y la invasión de tierras tanto en zonas rurales como urbanas por campesinos o grupos vulnerables, algunas veces apoyados por grupos políticos, como en los alrededores de las áreas de reserva de la Sierra de Guadalupe, en el Estado de México.
Analiza un conflicto territorial que tiene lugar en el sureste mexicano.
Este conflicto se desarrolla entre los estados de Oaxaca y Chiapas por la posesión de una región de gran riqueza natural, hablamos de la región de los Chimalapas.
En el sureste mexicano, es en donde predominan las regiones de selva y bosque en el país, regiones que cuentan con un alto grado de biodiversidad.
La región de los Chimalapas se encuentra en el corazón del Istmo de Tehuantepec, en el oriente del estado de Oaxaca; y se destaca por ser el lugar cuyas selvas húmedas y bosques mesófilos se encuentran en muy buen estado de conservación, por lo que es la zona de mayor biodiversidad de México.
Incluso, en el año 2014, se estimó que dicha región produjo 40% de los escurrimientos pluviales del país, es decir que esta área de 595, 000 hectáreas fue responsable de producir casi la mitad de los escurrimientos pluviales en el territorio nacional.
Además, en esta región nacen los ríos Coatzacoalcos, Uxpanapa y Tonalá.
Chimalapas, en náhuatl significa: "agua de los escudos", y en lengua zoque quiere decir: "jícara de oro".
Sin duda estos nombres hacen referencia a su gran riqueza natural.
Ahora, para que conozcas acerca de esa riqueza natural de los Chimalapas, te invito a ver y escuchar el siguiente audiovisual. Observa del minuto 00:08 al 04:05.
- Chimalapas, Una ventana a las selvas húmedas.
https://www.youtube.com/watch?v=4cNPpZEPLGw
Cómo pudiste identificar en el audiovisual la región cuenta con una gran diversidad de flora y fauna.
La combinación de la selva húmeda y el bosque, propician que su biodiversidad sea abundante.
Si bien están presentes los dos tipos de regiones es común que, sólo se le llame la selva de los Chimalapas.
En esta región, la selva de los Chimalapas, están asentadas dos comunidades agrarias: Santa María y San Miguel; y son propiedad del pueblo indígena zoque chimalapa, descendiente de los olmecas.
Ambas comunidades están registradas desde la colonia como parte del territorio de Oaxaca.
Ya que los zoques oaxaqueños cuentan con un título de propiedad que confirma que la corona española les vendió sus tierras, 900 mil hectáreas de Santa María, por 25 mil pesos oro.
¿Cómo fue que se produjo el conflicto por las tierras en los Chimalapas?
Un primer incidente ocurrió en la década de 1940.
Cuando se estableció en la región una empresa maderera, de origen michoacano, que obtuvo concesiones para explotar los recursos forestales en las tierras comunales de los zoques de Santa María y San Miguel Chimalapa.
Eso debió ser una gran afrenta por el saqueo de sus tierras.
Pero, ¿cuándo comenzó el conflicto entre los estados vecinos: Oaxaca y Chiapas?
El conflicto por la selva de los Chimalapas comenzó en 1967 fecha en la que el gobierno federal concedió al estado de Chiapas 6, 000 hectáreas de esta región, localizadas en territorio oaxaqueño, y a la que llegaron asentamientos de tzotziles y zoques chiapanecos; lo que inconformó a los zoques oaxaqueños, y desde ese entonces la disputa persiste.
¿Te das cuenta de cuáles son las partes involucradas en este conflicto?
Se logra identificar a los pobladores, al gobierno federal que otorgó las tierras y a los gobiernos locales que entraron en disputa por la posesión de éstas.
Exacto, pero además que entre los pobladores están: la población originaria, zoques oaxaqueños; y por otro lado los pobladores que llegaron, los zoques y los tzotziles procedentes de Chiapas.
El conflicto se remonta a la concesión de estas tierras al pueblo y gobierno chiapaneco.
Aunque desde antes venían ocurriendo irregularidades como la entrada de empresas madereras, que se comentaron; y, posteriormente, se han ido sumando más y más acontecimientos que han vuelto más y más complejo el problema.
¿Y cuál fue la reacción del pueblo oaxaqueño zoque?
El pueblo oaxaqueño zoque lleva décadas protestando por la explotación de los recursos de la región, que involucra la deforestación y la tala indiscriminada de la selva debido a la sobreexplotación de dos recursos de gran valor: la caoba y el cedro.
La disputa por la posesión del territorio y el uso de los recursos de esta región, ha tenido como consecuencia enfrentamientos violentos entre oaxaqueños y chiapanecos. Por ejemplo, los zoques, oaxaqueños y dueños originarios de esas tierras llegaron a quemar algunos asentamientos chiapanecos por considerarlos invasores de sus tierras
Además, se han favorecido desacuerdos políticos entre los gobiernos de los estados.
Una consecuencia más, es la explotación desmedida de la selva y el bosque, la deforestación, y con ello la consecuente pérdida de biodiversidad.
¿Qué otro tipo de acciones tomaba la población que se sentía despojada de su tierra?
Cerraban los caminos para que no pasaran a la selva o al bosque los camiones de los taladores; o bien confiscaban los camiones que salían de la zona repletos de madera y otros productos forestales.
Defendían su territorio y sus recursos a toda costa y esto explica porque eran y son tierras comunales.
El término tierras comunales, se refiere a que de manera institucional una superficie de terreno se ha concedido como propiedad a un grupo de personas determinado; en este caso, a los zoques, lo que incluye las tierras, agua, bosques y otros recursos naturales.
Una variable más -que complicó el conflicto- fue que en el año 2008 se otorgaron alrededor de 7, 000 hectáreas de la comunidad de San Miguel, a una empresa canadiense para su exploración y explotación minera, cuya concesión tendría una duración de 50 años, por lo que culminaría hasta el 2058.
¿Y cuáles eran los intereses de la empresa minera?
Su propósito era extraer minerales como el oro, la plata y el cobre.
Esto desencadenó la oposición de los habitantes de las comunidades de Oaxaca, así como diversos grupos ambientalistas.
Lo destacable de esta situación es que se unieron todos los comuneros, es decir los comuneros zoques y los tzotziles pues ante el acecho de las empresas privadas unieron fuerzas para oponerse a la explotación de sus tierras y sus recursos.
Juntos protestaron y denunciaron la presencia de un enemigo común que atentaba contra los recursos de sus tierras.
Y de la conservación de la región, ya que es común que la extracción mineral conlleve la alteración de la vegetación natural, la contaminación de los cuerpos de agua del lugar y la contaminación del aire.
¿Y sí se instaló la mina?, ¿continúa operando?
No, ante la movilización de los habitantes de la región y la búsqueda incesante del diálogo con las autoridades, a fines del año pasado los gobiernos federal, estatal y local acordaron cancelar el proyecto minero y propusieron impulsar un proyecto ecoturístico en la región.
Se observan dos caminos para resolver el conflicto, ya que hubo momentos en los que se presentaron soluciones violentas y posteriormente se buscó la solución pacífica, a través del diálogo; pero supongo que siempre manteniéndose firmes y exigiendo sus derechos.
De hecho, el conflicto no se ha resuelto del todo, esto último -de la denuncia y rechazo a que se instalara la empresa minera y su resolución institucional-, sólo es una solución a una parte del conflicto.
¿Qué parte del conflicto aún persiste?
La lucha contra las empresas madereras por la explotación legal e ilegal de la selva y el bosque.
¿Cómo se pueden ordenar las ideas para hacer una síntesis de este conflicto?
Observa cómo elaborar un organizador gráfico en el que sintetizas las variables que componen la problemática.
Las variables que intervienen en el conflicto, para su análisis: su localización, las partes que intervienen; la causa o causas del conflicto; y las consecuencias.

Se comienza por señalar: en dónde se localiza el conflicto del que se ha estado hablando.
La zona en conflicto es la región de Los Chimalapas, en los límites estatales de Oaxaca y Chiapas. Ahora identifica las partes que intervienen en el conflicto.

Interviene la población que ahí se asienta, originalmente los dueños de esas tierras; los zoques oaxaqueños; también la población que llegó a habitar las tierras los zoques y tzotziles chiapanecos; están además el gobierno federal -que cedió las tierras-, los gobiernos estatales de Oaxaca y Chiapas; las empresas madereras; y, anotemos también, la empresa minera que sabemos que estuvo interesada en la región, aunque por el momento detuvieron su proyecto.

Continúa con las causas que propiciaron el conflicto:
La concesión de tierras comunales de Oaxaca a Chiapas, la extracción ilegal de los recursos forestales; la sobreexplotación forestal y la posible extracción minera.

El enfrentamiento entre pueblos hermanos, zoques oaxaqueños y tzotziles y zoques chiapanecos; la quema de casas; enfrentamientos violentos con las empresas madereras, bloqueo de caminos, decomiso de camiones, con el saqueo de los recursos de la región; explotación excesiva de la selva y el bosque, deforestación y pérdida de biodiversidad.

Agrega recortes o dibujos para que sea un trabajo más completo.
El análisis de este tipo de conflictos, desde la perspectiva de la Geografía, deja ver el entramado de los componentes del espacio geográfico.
Por un lado, se tiene un lugar: los Chimalapas, ubicado en una región con gran riqueza de flora y fauna; además de yacimientos minerales; esto corresponde al componente natural.
¿Qué otro componente identificas en el conflicto?
Podría ser el componente social representado por los habitantes originales de la zona; y los nuevos pobladores que arribaron cuando les cedieron parte de esas tierras.
También interviene el componente político representado por la intervención de los gobiernos federal, estatal y local; así como el activismo de los comuneros y campesinos.
Igualmente está presente el componente económico, constituido por las negociaciones monetarias motivadas por las empresas.
Recuerda las preguntas que se plantearon al inicio, reflexiona en ellas y respóndelas.
Considera que puedes seguir investigando más sobre el tema de los conflictos territoriales en tu libro de texto.
Si quieres saber más acerca de esta región de los Chimalapas y su problemática, pueden ver la entrevista realizada a una habitante y activista de esa zona en el video "Guardianes de los Chimalapas", Revista de la Universidad; lo pueden encontrar en la página: