MATEMÁTICAS - SECUNDARIA 1
Variación lineal y su representación tabular
(MAR 20 OCT)
ACTIVIDAD:
Para este reto, retomaremos el último problema de la lección.
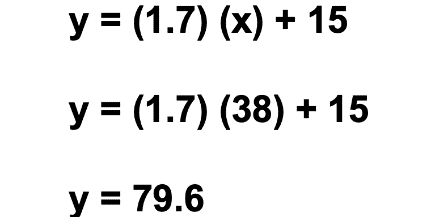
Este último resultado sigue siendo menor a 100, por lo que te retamos a encontrar el tiempo que tarda la batería del celular en cargar al 100%.
No olvides considerar que la máxima carga de batería es al 100% y, en ese momento, desconectar el celular para evitar un consumo innecesario de energía eléctrica.
RESUMEN:
Para comenzar reflexiona sobre las siguientes preguntas:
Alguna vez te has preguntado si existe una relación entre…
- ¿... el tiempo y el porcentaje de carga de un celular?
- ¿... la relación entre el tiempo y los litros de agua vertidos en un tinaco vacío?
- ¿... la relación del tiempo de llenado de un depósito de agua con cierto volumen inicial y la capacidad de bombeo?
- ¿... el costo en relación con los días de renta de un automóvil, con un depósito inicial?
Reflexiona en torno a estas preguntas para comprender mejor la relación que las magnitudes implicadas guardan entre sí.
Dicha relación se puede representar y analizar en tablas. Esto es algo que ya has hecho cuando calculas la variación entre dos magnitudes distintas.
Analicemos la siguiente situación:
El tinaco de una casa tiene capacidad de 1 200 litros; el manual de la bomba de agua dice que se vierten 80 litros por cada minuto, ¿cuánto tiempo tardaría en llenarse el tinaco?
Analicemos en una tabla los datos, comparando los minutos transcurridos y los litros de agua que se depositan en el tinaco.
En la primera columna tenemos el tiempo en minutos, los cuales son 1, 2, 3, 5, y escribimos “x”, que representa el tiempo de llenado del tinaco, y que es el dato desconocido. En la segunda columna ubicamos la capacidad en litros, cuyos valores son 80, 160, 240, 400 y 1 200 litros.
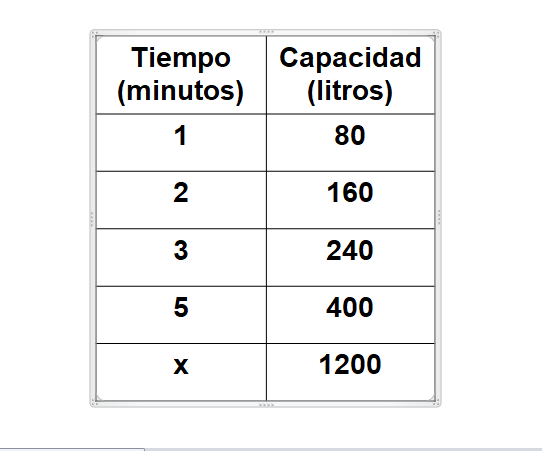
En la tabla podemos relacionar los minutos transcurridos con la cantidad de litros vertidos en el tinaco, esto nos ayudará a calcular los minutos que deben transcurrir para que el tinaco se llene.
Recuerda que en el manual se indica que la bomba vierte 80 litros por minuto, así que este valor es la constante de variación que, en este caso, también es de proporcionalidad, y queremos calcular los minutos que tardará en llenarse un tinaco de 1 200 litros.
Analicemos qué sucede al dividir los litros “y” que aparecen en la tabla, entre la constante de variación “k”. La constante de variación “k” es la constante de proporcionalidad.
Agregamos a la tabla anterior una tercera columna para analizar la relación entre las magnitudes de nuestro problema, para lo cual dividimos cada uno de los litros vertidos entre la constante de variación:
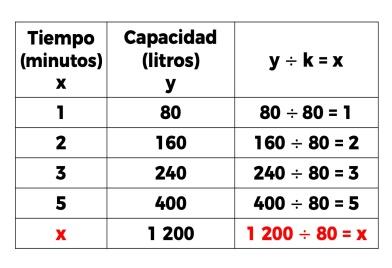
Observemos que, al realizar la división de cada uno de los datos que están en la segunda columna entre la constante de variación, se obtienen los minutos que se observan en la primera columna.
Por lo tanto, al obtener el cociente de 1 200 entre la constante de variación, que es 80, obtenemos los minutos que tardará en llenarse el tinaco, en este caso, 15 minutos, que es el valor faltante en nuestra tabla.

Esta constante de variación es importante para determinar cualquier valor desconocido de una u otra magnitud relacionadas entre sí, conociendo una de ellas.
Para este caso, esta constante recibe el nombre de constante de variación o de proporcionalidad.
Ahora analicemos la siguiente situación:
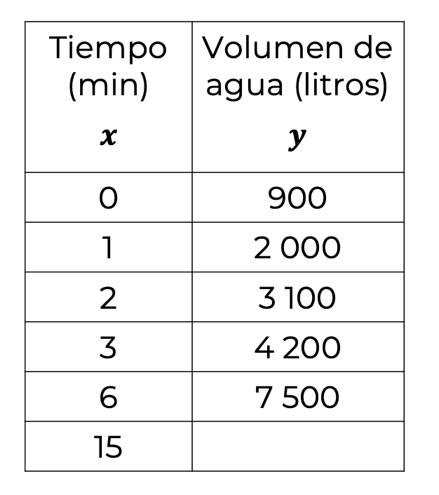
El depósito de agua que se construyó en una población, tiene un volumen de 24 000 litros de capacidad para abastecer a todos los hogares. El gobierno de la localidad les donó una bomba con una capacidad de abastecimiento de 1 100 litros por minuto y le instalaron un sistema automático que se activa cuando el depósito baja a un nivel de
900 litros para que los pobladores no se queden sin agua en ningún momento. El ingeniero que realizó la instalación de la bomba dejó la siguiente tabla:

En esta tabla se especifican los minutos transcurridos, representados con “x” en la primera columna, los cuales son 0, 1, 2, 3, 6 y 15. Mientras que en la segunda columna se indica el volumen de agua, representada con “y”, que se vierte en el depósito, que son 900, 2 000, 3 100, 4 200 y 7 500 litros, y como observas en el último renglón, únicamente se indican los minutos que trabaja la bomba, pero falta el dato del volumen correspondiente a dicho tiempo, ¿cómo calcularías el volumen de agua que tendrá el depósito en esos 15 minutos?
Para responder a esta pregunta, observa el siguiente video que plantea algo muy parecido a esta situación.
- Gráficas de los movimientos
Matemáticas 1, Bloque 2
Del minuto: 0:22 a 0:55
https://www.youtube.com/watch?v=MA81aT3LnMs&feature=youtu.be
De acuerdo con el video, y analizando los datos que se presentan en la tabla, se puede determinar el volumen en litros de agua que tendrá el depósito al transcurrir 15 minutos después de haberse activado el encendido automático de la bomba. Entonces, analicemos la tabla para determinar cómo se calculan los litros en relación con el tiempo transcurrido en minutos.
Para esto, ya sabemos dos datos: los litros de bombeo por minuto, los cuales son 1 100, tomando en cuenta que ese bombeo siempre es el mismo, el cual representa la constante de variación, y que el encendido automático de la bomba se activa cuando quedan 900 litros en el depósito.
Es importante considerar que, cuando el depósito tiene 900 litros de agua, la bomba se activa y ese breve instante se considera como el minuto 0. Por lo que 1 100 litros los multiplicamos por el minuto 0 y al resultado le sumamos 900 para obtener los 900 litros iniciales.
Transcurrido el primer minuto, la bomba ha mandado al depósito 1 100 litros, que es la constante de variación, por lo que escribimos 1 100 por 1 más los 900 litros que contenía inicialmente el depósito; da un total de 2 000 litros de agua. Para el segundo minuto, se multiplica la constante de variación por 2, más los 900 litros iniciales, obteniendo 3 100 litros. En el minuto 3 multiplicamos 1 100 por 3 y al producto le sumamos 900; da como resultado 4 200. Para el minuto 6, multiplicamos 1 100 por 6, y al resultado se le suman 900, obteniendo así 7 500.
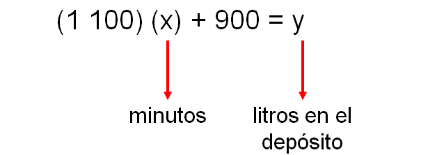
Observa que lo que está cambiando son los minutos y la cantidad de agua que llena el tinaco; es decir, son los únicos que presentan variación y tanto la constante de variación como los litros iniciales que contenía el depósito al instante de encender la bomba, son magnitudes fijas. Tomando como referencia esta relación determinamos el total de litros que habrá en 15 minutos multiplicando 15 por 1 100, y a este producto le sumamos 900, obteniendo 17 400 litros.
15 X 1100 + 900 = 17400
Tomando en cuenta lo antes descrito, podemos determinar el total de litros en el depósito para cualquier minuto utilizando una expresión que generalizamos de la siguiente manera:
Te invitamos a buscar en tu libro de texto el aprendizaje esperado que has estado trabajando durante esta lección, encontrarás información complementaria como la siguiente:
“Cuando una cantidad depende o se relaciona con otra de manera proporcional, se dice que entre ellas se establece una variación directamente proporcional entre ambas cantidades. En dicha relación, las cantidades que cambian se llaman variables, y las cantidades que no cambian se denominan constantes. En estos casos, cuando conocemos el valor de una variable, es posible determinar el de la otra. Por ello, la primera se conoce como variable independiente y la segunda, como variable dependiente.”
De acuerdo con la información que acabas de leer, en la situación anterior podemos identificar que el total de litros que tendrá el depósito dependerá del tiempo que esté encendida la bomba.
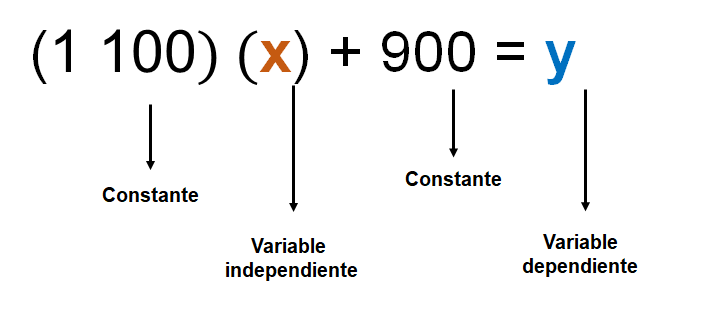
Por tal motivo, la variable dependiente son los litros resultantes en el depósito y la variable independiente son los minutos transcurridos.
Asimismo, podemos identificar las magnitudes que son constantes; en este caso, la cantidad de litros que se vierte por cada minuto y los litros que inicialmente tiene el depósito.
En las dos situaciones anteriores hemos identificado la constante de variación proporcional, la cual se usa para calcular una de las dos variables que están relacionadas entre sí, aun cuando se tenga una condición inicial. Mientras que en el primer caso, la constante de variación era la constante de proporcionalidad. No ocurre así en el segundo caso, donde existe una cantidad inicial.
El tema de esta lección puede aplicarse en múltiples situaciones, una de ellas es, por ejemplo, en las agencias donde rentan autos. Algunas agencias cobran una cantidad base más una renta por día, sin importar el kilometraje.
Aquí, en la Ciudad de México, una conocida agencia ofrece su servicio con un costo actual de $108 por día, más un pago único de $550 por el seguro de viaje.
Al contratar el servicio, la agencia incluye una tabla en donde se muestra lo que se debe pagar por la renta del automóvil por un determinado número de días.
Con esta información, respondamos a la pregunta: ¿cuánto pagaremos por el uso del automóvil durante 7 días?
Para ayudarnos a responder la pregunta anterior, analicemos la tabla en donde están concentrados algunos datos, y de esta manera podremos calcular el costo que se debe pagar por 7 días de renta.
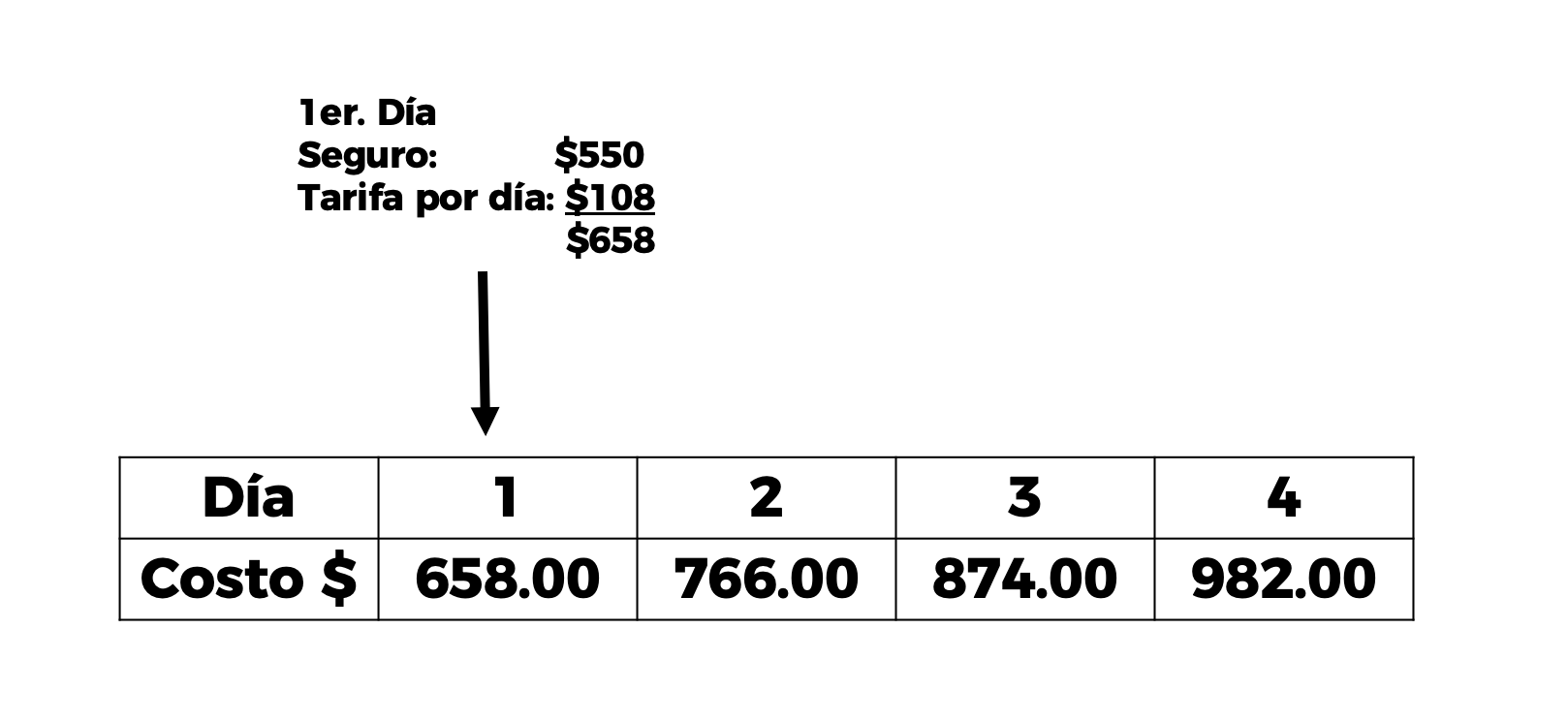
Observa que en la primera fila tenemos los días que utilizaremos el automóvil, que son 1, 2, 3 y 4, respectivamente. Mientras que en la segunda fila tenemos el costo que corresponde a los días que utilizaremos el servicio, es decir, 658, 766, 874, 982 y 1 090 pesos, respectivamente.
De acuerdo con estos datos, ¿pudiste identificar las variables y las constantes?
En este caso, el total que se debe pagar está relacionado con los días de renta, por lo tanto, el costo total depende de los días que rentamos el automóvil.
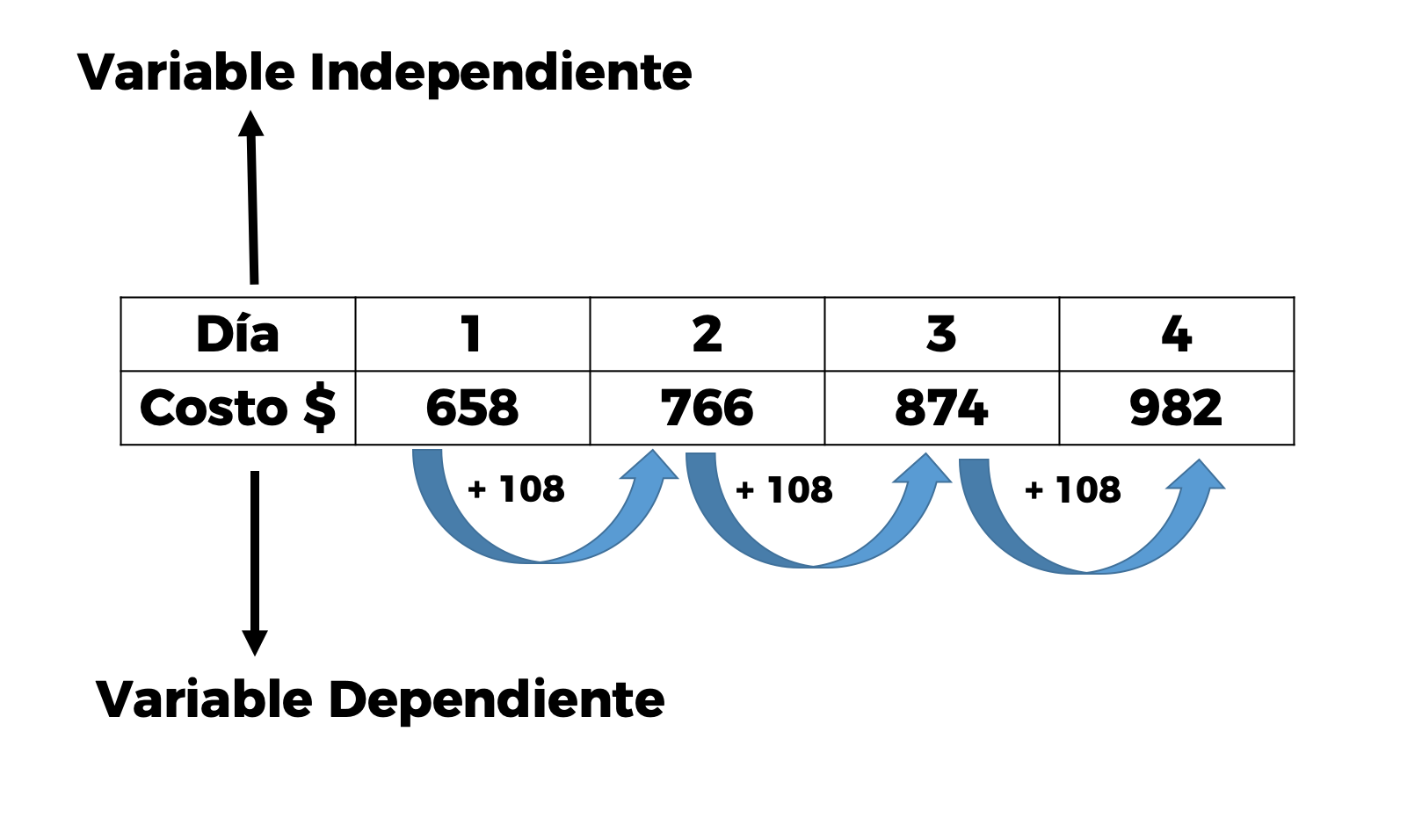
Entonces, podemos afirmar que la variable dependiente es el costo total y la variable independiente son los días de renta.
Por otro lado, en este problema hay dos datos que no cambian. El pago del seguro, que es de $550, corresponde a la cantidad o condición inicial, y el costo fijo de $108 por cada día que se renta el automóvil; este último hace variar el costo por los días rentados, razón por la cual se le llama constante de variación.
Esta situación representa una variación lineal, pues las dos cantidades aumentan o disminuyen en la misma proporción, por lo tanto, observamos que la relación entre las dos magnitudes de nuestro problema aumentan de 108 en 108. A esta relación se le llama lineal.
De acuerdo con lo establecido anteriormente, se puede calcular el costo para cualquier cantidad de días contratados en la renta de un automóvil mediante la siguiente expresión:
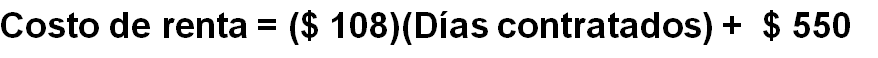
De esta manera, podemos responder la pregunta inicial: ¿cuánto pagaremos por el uso del automóvil durante 7 días?

Observa que en cada uno de los casos siempre hay dos magnitudes que se relacionan.
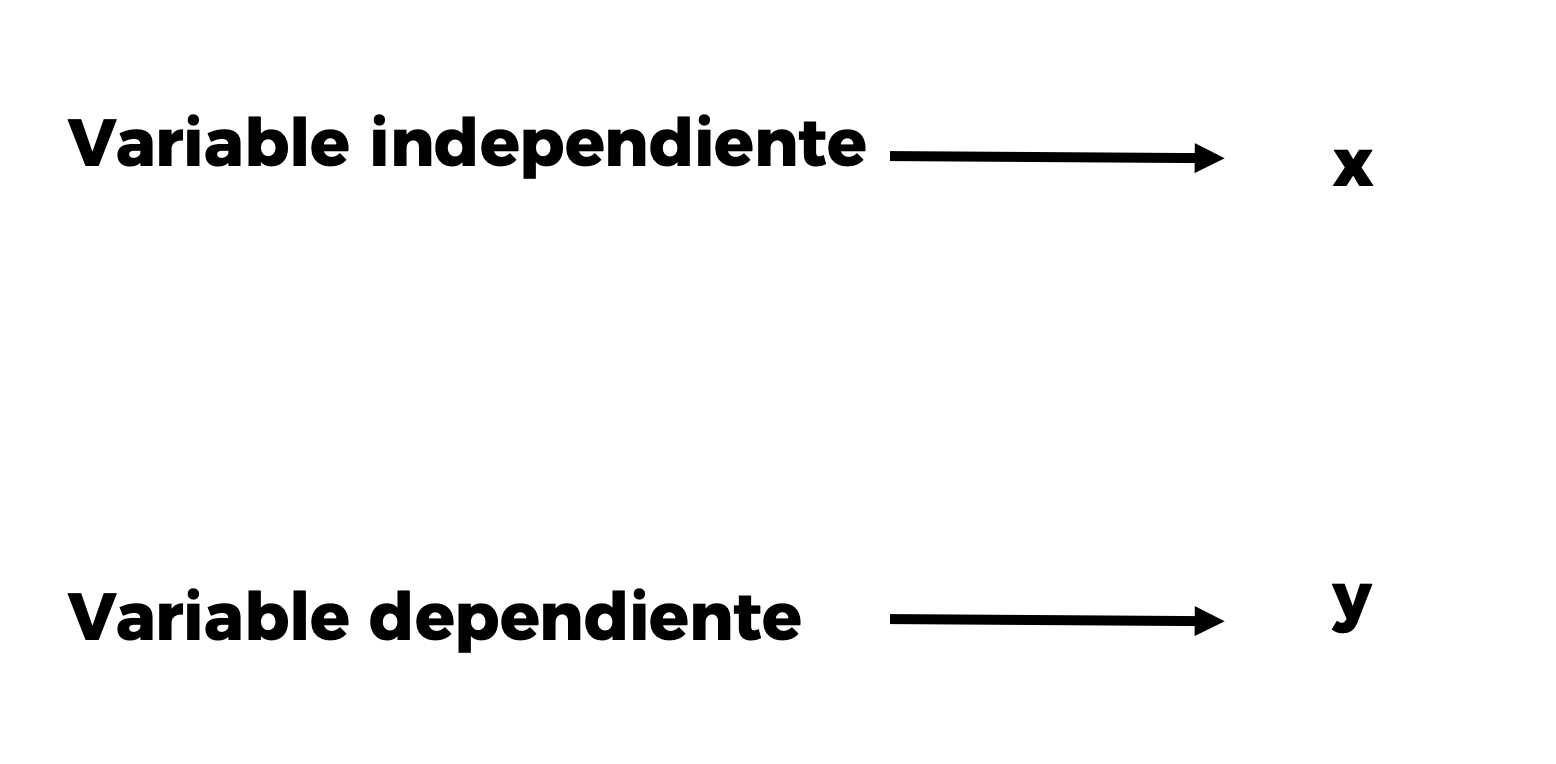
Si una de las magnitudes adquiere un valor que depende del valor de la otra, se le designa como variable dependiente, la cual podemos expresar mediante la letra “y”.
A la magnitud que no depende del valor de la otra se le conoce como variable independiente, la cual podemos expresar mediante la letra “x”.
Recuerda que en esta lección estas estudiando el significado de la variación lineal de una situación problemática mediante el análisis de los datos concentrados en una tabla. Observa que en el problema del tinaco la constante de variación es la misma que la constante de proporcionalidad, ya que no hay una condición inicial, puesto que partimos de 0.
En problemas donde sí hay una condición inicial, debemos considerarla para determinar la variación que existe entre los datos proporcionados.
El problema que acabas de ver es un ejemplo de ello, en donde antes de comenzar a utilizar el auto, debe cubrirse una cierta cantidad por el seguro, por lo que no se parte de 0.
Considerando lo visto en esta lección, podemos decir que estos conceptos también los podemos aplicar en casa. Por ejemplo, la necesidad de utilizar con mayor frecuencia el celular debido al aislamiento voluntario por la contingencia sanitaria, por lo cual es necesario optimizar el tiempo de carga, es decir, medir el tiempo que tarda la pila del celular en cargar al 100%, y así no generar un consumo de electricidad innecesario. Es recomendable no dejar que la batería se descargue totalmente para que dure más tiempo, por lo cual se debe poner a cargar el celular cuando aún tiene 15% de batería.
Para poder conocer el tiempo que tarda en cargarse completamente la batería del celular, analicemos la siguiente tabla:
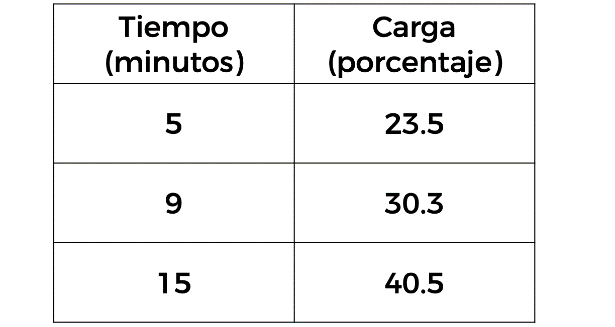
En la primera columna se muestran los minutos transcurridos, que son 5, 9 y 15, mientras que en la segunda columna tenemos la carga, mostrada en porcentaje, que corresponde a 23.5, 30.3 y 40.5.
La carga está aumentando al igual que los minutos, y también la carga aumenta dependiendo de los minutos que esté administrando energía al celular. Por lo que podemos afirmar que el porcentaje de la carga varía dependiendo de los minutos, en consecuencia, el porcentaje de la carga es la variable dependiente, y la podemos representar con la letra “y”.
Entonces, la otra cantidad que está variando son los minutos durante los cuales el celular recibe energía, por lo que los minutos son la variable independiente y la representaremos con la letra “x”. Como se muestra en la siguiente tabla:

Para determinar la constante de variación analicemos las variables:
Consideremos dos pares de datos de la tabla y obtengamos su variación; por ejemplo, cuando han transcurrido 5 minutos, la carga marca 23.5%, y cuando han transcurrido 9 minutos, la batería marca 30.3%.
Para determinar la constante de variación, encontremos la diferencia de sus variables:
Para la variable de los minutos, restamos 9 menos 5 = 4. Y para la variable del porcentaje de carga, restamos 30.3 menos 23.5 = 6.8. Finalmente dividimos el resultado de la variación de porcentaje de carga entre el resultado de la variación de los minutos. Es decir, dividimos 6.8 entre 4 = 1.7; esta es la constante de variación.

Comprobemos en otro par de datos:
Si han transcurrido 9 minutos, el porcentaje de carga es de 30.3. Y al transcurrir 15 minutos el porcentaje de carga es de 40.5. Encontremos la variación entre magnitudes de la misma variable restando las dos seleccionadas.
Para los minutos, que corresponden a la variable independiente, restamos 15 menos 9 = 6. En relación con el porcentaje de carga, que es la variable dependiente, restamos sus correspondientes valores 40.5 menos 30.3 = 10.2. Determinemos la constante dividiendo los dos resultados: 10.2 entre 6 = 1.7.

Con lo anterior podemos concluir que existe una variación que es constante, cuyo valor es de 1.7, y de acuerdo con lo estudiado en esta lección, la llamamos constante de variación, la cual nos indica que la carga es constante minuto a minuto; esto es, que la carga se incrementa 1.7% por cada minuto.
Recuerda que, para este problema, existe una condición inicial, que es la carga de 15% que el teléfono tiene antes de comenzar a recibir energía.
De acuerdo con la tabla, en el minuto 5 el teléfono registra una carga de 23.5%; este valor se obtiene de multiplicar la constante de variación 1.7 por el minuto 5, y al resultado se le suma la condición inicial de 15% de batería. Para el minuto 9, la carga del teléfono es de 30.3%, que es resultado de multiplicar 1.7 por 9, más 15. Para el minuto 15, la carga del teléfono es de 40.5%, que es resultado de multiplicar 1.7 por 15, más 15.

Por lo tanto, la condición para calcular el porcentaje de carga en el celular para cualquier minuto es multiplicar la constante de variación (1.7) por los minutos transcurridos, más la condición inicial 15. Se obtiene así la siguiente expresión:
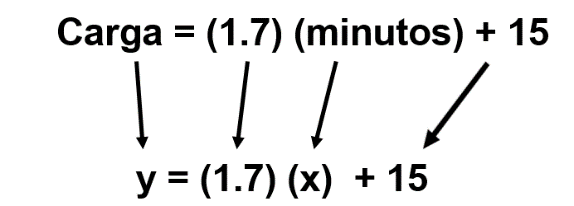
En un principio determinamos que los minutos son la variable independiente, a la cual llamamos “x”, y la carga, la variable dependiente, a la cual llamamos “y”. Entonces podemos escribir la expresión aritmética de tal forma que, en lugar de escribir minutos, escribimos “x”, y en lugar de escribir carga, escribimos “y”; queda de la siguiente manera:
y = (1.7) (x) + 15
Ahora ocuparemos esta última expresión para calcular el nivel de carga que tendrá el celular transcurridos 25 minutos.
Recuerda que, en este caso, el tiempo corresponde a la variable independiente “x”. A dicha variable podemos asignarle valores, puesto que la “y” depende directamente de ella.
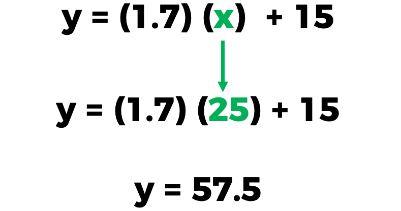
En dicha expresión sustituimos la variable independiente “x” por los minutos que han transcurrido, en este caso, 25.
Ahora resolvemos las operaciones resultantes tomando en cuenta la jerarquía de operaciones, es decir, el producto de 1.7 por 25 más 15, que da como resultado 57.5.
Este resultado nos indica que a los 25 minutos el celular registra una carga de 57.5%.
Realicemos otro cálculo para determinar la carga que tendrá la batería del celular después de estar conectado durante 38 minutos.
Para conocer la carga en el minuto 38, realicemos el procedimiento anterior: multiplicamos 1.7 por 38, al producto le sumamos 15, lo que nos da como resultado 79.6.
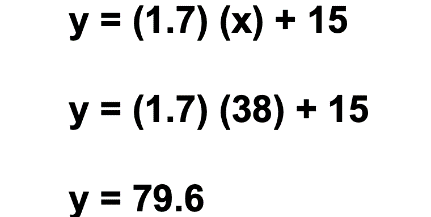
En esta lección resolviste situaciones problemáticas concentrando los datos en tablas. Esta estrategia te permitió realizar un análisis de la variación entre sus magnitudes correspondientes. Identificaste:
- La variable independiente. Recuerda que este valor no depende de otro.
- La variable dependiente, cuyo valor depende de otro.
- La constante de variación, en donde dicho valor es constante y representa la variación entre las magnitudes.
En cada uno de los casos que analizaste, determinaste que dos variables se relacionan de tal manera que la variación de una magnitud respecto de la otra se le conoce como constante de variación, existiendo o no una condición inicial.
Cuando las variables aumentan o disminuyen simultáneamente de manera constante, implica que existe una relación lineal entre ellas, lo que significa que es una variación lineal.
Con los elementos que identificaste y el valor de la condición inicial, si está presente en el planteamiento del problema, se genera una expresión aritmética con la cual puedes calcular el valor de la variable dependiente, dando diferentes valores a la variable independiente.
En las situaciones que desarrollaste a lo largo de esta lección los datos de las variables que intervienen se encuentran relacionados entre sí. Sin embargo, no son las únicas circunstancias en las cuales puedes aplicar estos conceptos.
Por ejemplo, los antropólogos pueden determinar la estatura de una persona con sólo medir el largo del fémur, ya que entre estas magnitudes existe una relación de variación lineal.
En el ámbito de la Geometría se emplea para calcular las medidas de un círculo en donde el diámetro es la variable independiente, mientras que el valor de la circunferencia varía; aquí consideramos el valor de pi = 3.1416 y que se mantiene constante, lo cual representa la constante de variación.
Para este reto, retomaremos el último problema de la lección.
Este último resultado sigue siendo menor a 100, por lo que te retamos a encontrar el tiempo que tarda la batería del celular en cargar al 100%.
No olvides considerar que la máxima carga de batería es al 100% y, en ese momento, desconectar el celular para evitar un consumo innecesario de energía eléctrica.
Para comenzar reflexiona sobre las siguientes preguntas:
Alguna vez te has preguntado si existe una relación entre…
- ¿... el tiempo y el porcentaje de carga de un celular?
- ¿... la relación entre el tiempo y los litros de agua vertidos en un tinaco vacío?
- ¿... la relación del tiempo de llenado de un depósito de agua con cierto volumen inicial y la capacidad de bombeo?
- ¿... el costo en relación con los días de renta de un automóvil, con un depósito inicial?
Reflexiona en torno a estas preguntas para comprender mejor la relación que las magnitudes implicadas guardan entre sí.
Dicha relación se puede representar y analizar en tablas. Esto es algo que ya has hecho cuando calculas la variación entre dos magnitudes distintas.
Analicemos la siguiente situación:
El tinaco de una casa tiene capacidad de 1 200 litros; el manual de la bomba de agua dice que se vierten 80 litros por cada minuto, ¿cuánto tiempo tardaría en llenarse el tinaco?
Analicemos en una tabla los datos, comparando los minutos transcurridos y los litros de agua que se depositan en el tinaco.
En la primera columna tenemos el tiempo en minutos, los cuales son 1, 2, 3, 5, y escribimos “x”, que representa el tiempo de llenado del tinaco, y que es el dato desconocido. En la segunda columna ubicamos la capacidad en litros, cuyos valores son 80, 160, 240, 400 y 1 200 litros.

En la tabla podemos relacionar los minutos transcurridos con la cantidad de litros vertidos en el tinaco, esto nos ayudará a calcular los minutos que deben transcurrir para que el tinaco se llene.
Recuerda que en el manual se indica que la bomba vierte 80 litros por minuto, así que este valor es la constante de variación que, en este caso, también es de proporcionalidad, y queremos calcular los minutos que tardará en llenarse un tinaco de 1 200 litros.
Analicemos qué sucede al dividir los litros “y” que aparecen en la tabla, entre la constante de variación “k”. La constante de variación “k” es la constante de proporcionalidad.
Agregamos a la tabla anterior una tercera columna para analizar la relación entre las magnitudes de nuestro problema, para lo cual dividimos cada uno de los litros vertidos entre la constante de variación:

Observemos que, al realizar la división de cada uno de los datos que están en la segunda columna entre la constante de variación, se obtienen los minutos que se observan en la primera columna.
Por lo tanto, al obtener el cociente de 1 200 entre la constante de variación, que es 80, obtenemos los minutos que tardará en llenarse el tinaco, en este caso, 15 minutos, que es el valor faltante en nuestra tabla.

Esta constante de variación es importante para determinar cualquier valor desconocido de una u otra magnitud relacionadas entre sí, conociendo una de ellas.
Para este caso, esta constante recibe el nombre de constante de variación o de proporcionalidad.
Ahora analicemos la siguiente situación:
El depósito de agua que se construyó en una población, tiene un volumen de 24 000 litros de capacidad para abastecer a todos los hogares. El gobierno de la localidad les donó una bomba con una capacidad de abastecimiento de 1 100 litros por minuto y le instalaron un sistema automático que se activa cuando el depósito baja a un nivel de
900 litros para que los pobladores no se queden sin agua en ningún momento. El ingeniero que realizó la instalación de la bomba dejó la siguiente tabla:

En esta tabla se especifican los minutos transcurridos, representados con “x” en la primera columna, los cuales son 0, 1, 2, 3, 6 y 15. Mientras que en la segunda columna se indica el volumen de agua, representada con “y”, que se vierte en el depósito, que son 900, 2 000, 3 100, 4 200 y 7 500 litros, y como observas en el último renglón, únicamente se indican los minutos que trabaja la bomba, pero falta el dato del volumen correspondiente a dicho tiempo, ¿cómo calcularías el volumen de agua que tendrá el depósito en esos 15 minutos?
Para responder a esta pregunta, observa el siguiente video que plantea algo muy parecido a esta situación.
- Gráficas de los movimientos
Matemáticas 1, Bloque 2
Del minuto: 0:22 a 0:55
https://www.youtube.com/watch?v=MA81aT3LnMs&feature=youtu.be
De acuerdo con el video, y analizando los datos que se presentan en la tabla, se puede determinar el volumen en litros de agua que tendrá el depósito al transcurrir 15 minutos después de haberse activado el encendido automático de la bomba. Entonces, analicemos la tabla para determinar cómo se calculan los litros en relación con el tiempo transcurrido en minutos.
Para esto, ya sabemos dos datos: los litros de bombeo por minuto, los cuales son 1 100, tomando en cuenta que ese bombeo siempre es el mismo, el cual representa la constante de variación, y que el encendido automático de la bomba se activa cuando quedan 900 litros en el depósito.
Es importante considerar que, cuando el depósito tiene 900 litros de agua, la bomba se activa y ese breve instante se considera como el minuto 0. Por lo que 1 100 litros los multiplicamos por el minuto 0 y al resultado le sumamos 900 para obtener los 900 litros iniciales.
Transcurrido el primer minuto, la bomba ha mandado al depósito 1 100 litros, que es la constante de variación, por lo que escribimos 1 100 por 1 más los 900 litros que contenía inicialmente el depósito; da un total de 2 000 litros de agua. Para el segundo minuto, se multiplica la constante de variación por 2, más los 900 litros iniciales, obteniendo 3 100 litros. En el minuto 3 multiplicamos 1 100 por 3 y al producto le sumamos 900; da como resultado 4 200. Para el minuto 6, multiplicamos 1 100 por 6, y al resultado se le suman 900, obteniendo así 7 500.

Observa que lo que está cambiando son los minutos y la cantidad de agua que llena el tinaco; es decir, son los únicos que presentan variación y tanto la constante de variación como los litros iniciales que contenía el depósito al instante de encender la bomba, son magnitudes fijas. Tomando como referencia esta relación determinamos el total de litros que habrá en 15 minutos multiplicando 15 por 1 100, y a este producto le sumamos 900, obteniendo 17 400 litros.
15 X 1100 + 900 = 17400
Tomando en cuenta lo antes descrito, podemos determinar el total de litros en el depósito para cualquier minuto utilizando una expresión que generalizamos de la siguiente manera:

Te invitamos a buscar en tu libro de texto el aprendizaje esperado que has estado trabajando durante esta lección, encontrarás información complementaria como la siguiente:
“Cuando una cantidad depende o se relaciona con otra de manera proporcional, se dice que entre ellas se establece una variación directamente proporcional entre ambas cantidades. En dicha relación, las cantidades que cambian se llaman variables, y las cantidades que no cambian se denominan constantes. En estos casos, cuando conocemos el valor de una variable, es posible determinar el de la otra. Por ello, la primera se conoce como variable independiente y la segunda, como variable dependiente.”
De acuerdo con la información que acabas de leer, en la situación anterior podemos identificar que el total de litros que tendrá el depósito dependerá del tiempo que esté encendida la bomba.

Por tal motivo, la variable dependiente son los litros resultantes en el depósito y la variable independiente son los minutos transcurridos.
Asimismo, podemos identificar las magnitudes que son constantes; en este caso, la cantidad de litros que se vierte por cada minuto y los litros que inicialmente tiene el depósito.
En las dos situaciones anteriores hemos identificado la constante de variación proporcional, la cual se usa para calcular una de las dos variables que están relacionadas entre sí, aun cuando se tenga una condición inicial. Mientras que en el primer caso, la constante de variación era la constante de proporcionalidad. No ocurre así en el segundo caso, donde existe una cantidad inicial.
El tema de esta lección puede aplicarse en múltiples situaciones, una de ellas es, por ejemplo, en las agencias donde rentan autos. Algunas agencias cobran una cantidad base más una renta por día, sin importar el kilometraje.
Aquí, en la Ciudad de México, una conocida agencia ofrece su servicio con un costo actual de $108 por día, más un pago único de $550 por el seguro de viaje.
Al contratar el servicio, la agencia incluye una tabla en donde se muestra lo que se debe pagar por la renta del automóvil por un determinado número de días.
Con esta información, respondamos a la pregunta: ¿cuánto pagaremos por el uso del automóvil durante 7 días?
Para ayudarnos a responder la pregunta anterior, analicemos la tabla en donde están concentrados algunos datos, y de esta manera podremos calcular el costo que se debe pagar por 7 días de renta.

Observa que en la primera fila tenemos los días que utilizaremos el automóvil, que son 1, 2, 3 y 4, respectivamente. Mientras que en la segunda fila tenemos el costo que corresponde a los días que utilizaremos el servicio, es decir, 658, 766, 874, 982 y 1 090 pesos, respectivamente.
De acuerdo con estos datos, ¿pudiste identificar las variables y las constantes?
En este caso, el total que se debe pagar está relacionado con los días de renta, por lo tanto, el costo total depende de los días que rentamos el automóvil.

Entonces, podemos afirmar que la variable dependiente es el costo total y la variable independiente son los días de renta.
Por otro lado, en este problema hay dos datos que no cambian. El pago del seguro, que es de $550, corresponde a la cantidad o condición inicial, y el costo fijo de $108 por cada día que se renta el automóvil; este último hace variar el costo por los días rentados, razón por la cual se le llama constante de variación.
Esta situación representa una variación lineal, pues las dos cantidades aumentan o disminuyen en la misma proporción, por lo tanto, observamos que la relación entre las dos magnitudes de nuestro problema aumentan de 108 en 108. A esta relación se le llama lineal.
De acuerdo con lo establecido anteriormente, se puede calcular el costo para cualquier cantidad de días contratados en la renta de un automóvil mediante la siguiente expresión:
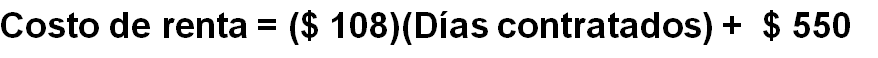
De esta manera, podemos responder la pregunta inicial: ¿cuánto pagaremos por el uso del automóvil durante 7 días?

Observa que en cada uno de los casos siempre hay dos magnitudes que se relacionan.

Si una de las magnitudes adquiere un valor que depende del valor de la otra, se le designa como variable dependiente, la cual podemos expresar mediante la letra “y”.
A la magnitud que no depende del valor de la otra se le conoce como variable independiente, la cual podemos expresar mediante la letra “x”.
Recuerda que en esta lección estas estudiando el significado de la variación lineal de una situación problemática mediante el análisis de los datos concentrados en una tabla. Observa que en el problema del tinaco la constante de variación es la misma que la constante de proporcionalidad, ya que no hay una condición inicial, puesto que partimos de 0.
En problemas donde sí hay una condición inicial, debemos considerarla para determinar la variación que existe entre los datos proporcionados.
El problema que acabas de ver es un ejemplo de ello, en donde antes de comenzar a utilizar el auto, debe cubrirse una cierta cantidad por el seguro, por lo que no se parte de 0.
Considerando lo visto en esta lección, podemos decir que estos conceptos también los podemos aplicar en casa. Por ejemplo, la necesidad de utilizar con mayor frecuencia el celular debido al aislamiento voluntario por la contingencia sanitaria, por lo cual es necesario optimizar el tiempo de carga, es decir, medir el tiempo que tarda la pila del celular en cargar al 100%, y así no generar un consumo de electricidad innecesario. Es recomendable no dejar que la batería se descargue totalmente para que dure más tiempo, por lo cual se debe poner a cargar el celular cuando aún tiene 15% de batería.
Para poder conocer el tiempo que tarda en cargarse completamente la batería del celular, analicemos la siguiente tabla:

En la primera columna se muestran los minutos transcurridos, que son 5, 9 y 15, mientras que en la segunda columna tenemos la carga, mostrada en porcentaje, que corresponde a 23.5, 30.3 y 40.5.
La carga está aumentando al igual que los minutos, y también la carga aumenta dependiendo de los minutos que esté administrando energía al celular. Por lo que podemos afirmar que el porcentaje de la carga varía dependiendo de los minutos, en consecuencia, el porcentaje de la carga es la variable dependiente, y la podemos representar con la letra “y”.
Entonces, la otra cantidad que está variando son los minutos durante los cuales el celular recibe energía, por lo que los minutos son la variable independiente y la representaremos con la letra “x”. Como se muestra en la siguiente tabla:

Para determinar la constante de variación analicemos las variables:
Consideremos dos pares de datos de la tabla y obtengamos su variación; por ejemplo, cuando han transcurrido 5 minutos, la carga marca 23.5%, y cuando han transcurrido 9 minutos, la batería marca 30.3%.
Para determinar la constante de variación, encontremos la diferencia de sus variables:
Para la variable de los minutos, restamos 9 menos 5 = 4. Y para la variable del porcentaje de carga, restamos 30.3 menos 23.5 = 6.8. Finalmente dividimos el resultado de la variación de porcentaje de carga entre el resultado de la variación de los minutos. Es decir, dividimos 6.8 entre 4 = 1.7; esta es la constante de variación.

Comprobemos en otro par de datos:
Si han transcurrido 9 minutos, el porcentaje de carga es de 30.3. Y al transcurrir 15 minutos el porcentaje de carga es de 40.5. Encontremos la variación entre magnitudes de la misma variable restando las dos seleccionadas.
Para los minutos, que corresponden a la variable independiente, restamos 15 menos 9 = 6. En relación con el porcentaje de carga, que es la variable dependiente, restamos sus correspondientes valores 40.5 menos 30.3 = 10.2. Determinemos la constante dividiendo los dos resultados: 10.2 entre 6 = 1.7.

Con lo anterior podemos concluir que existe una variación que es constante, cuyo valor es de 1.7, y de acuerdo con lo estudiado en esta lección, la llamamos constante de variación, la cual nos indica que la carga es constante minuto a minuto; esto es, que la carga se incrementa 1.7% por cada minuto.
Recuerda que, para este problema, existe una condición inicial, que es la carga de 15% que el teléfono tiene antes de comenzar a recibir energía.
De acuerdo con la tabla, en el minuto 5 el teléfono registra una carga de 23.5%; este valor se obtiene de multiplicar la constante de variación 1.7 por el minuto 5, y al resultado se le suma la condición inicial de 15% de batería. Para el minuto 9, la carga del teléfono es de 30.3%, que es resultado de multiplicar 1.7 por 9, más 15. Para el minuto 15, la carga del teléfono es de 40.5%, que es resultado de multiplicar 1.7 por 15, más 15.

Por lo tanto, la condición para calcular el porcentaje de carga en el celular para cualquier minuto es multiplicar la constante de variación (1.7) por los minutos transcurridos, más la condición inicial 15. Se obtiene así la siguiente expresión:
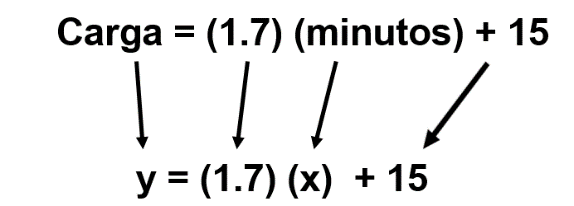
En un principio determinamos que los minutos son la variable independiente, a la cual llamamos “x”, y la carga, la variable dependiente, a la cual llamamos “y”. Entonces podemos escribir la expresión aritmética de tal forma que, en lugar de escribir minutos, escribimos “x”, y en lugar de escribir carga, escribimos “y”; queda de la siguiente manera:
y = (1.7) (x) + 15
Ahora ocuparemos esta última expresión para calcular el nivel de carga que tendrá el celular transcurridos 25 minutos.
Recuerda que, en este caso, el tiempo corresponde a la variable independiente “x”. A dicha variable podemos asignarle valores, puesto que la “y” depende directamente de ella.
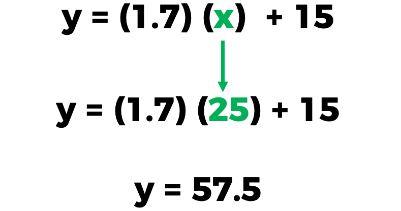
En dicha expresión sustituimos la variable independiente “x” por los minutos que han transcurrido, en este caso, 25.
Ahora resolvemos las operaciones resultantes tomando en cuenta la jerarquía de operaciones, es decir, el producto de 1.7 por 25 más 15, que da como resultado 57.5.
Este resultado nos indica que a los 25 minutos el celular registra una carga de 57.5%.
Realicemos otro cálculo para determinar la carga que tendrá la batería del celular después de estar conectado durante 38 minutos.
Para conocer la carga en el minuto 38, realicemos el procedimiento anterior: multiplicamos 1.7 por 38, al producto le sumamos 15, lo que nos da como resultado 79.6.
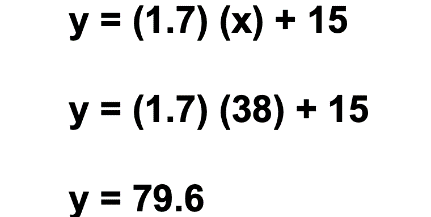
En esta lección resolviste situaciones problemáticas concentrando los datos en tablas. Esta estrategia te permitió realizar un análisis de la variación entre sus magnitudes correspondientes. Identificaste:
- La variable independiente. Recuerda que este valor no depende de otro.
- La variable dependiente, cuyo valor depende de otro.
- La constante de variación, en donde dicho valor es constante y representa la variación entre las magnitudes.
En cada uno de los casos que analizaste, determinaste que dos variables se relacionan de tal manera que la variación de una magnitud respecto de la otra se le conoce como constante de variación, existiendo o no una condición inicial.
Cuando las variables aumentan o disminuyen simultáneamente de manera constante, implica que existe una relación lineal entre ellas, lo que significa que es una variación lineal.
Con los elementos que identificaste y el valor de la condición inicial, si está presente en el planteamiento del problema, se genera una expresión aritmética con la cual puedes calcular el valor de la variable dependiente, dando diferentes valores a la variable independiente.
En las situaciones que desarrollaste a lo largo de esta lección los datos de las variables que intervienen se encuentran relacionados entre sí. Sin embargo, no son las únicas circunstancias en las cuales puedes aplicar estos conceptos.
Por ejemplo, los antropólogos pueden determinar la estatura de una persona con sólo medir el largo del fémur, ya que entre estas magnitudes existe una relación de variación lineal.
En el ámbito de la Geometría se emplea para calcular las medidas de un círculo en donde el diámetro es la variable independiente, mientras que el valor de la circunferencia varía; aquí consideramos el valor de pi = 3.1416 y que se mantiene constante, lo cual representa la constante de variación.