MATEMÁTICAS - SECUNDARIA 1
Sumas y restas de números enteros
(JUEVES 28 ENERO)
ACTIVIDAD:
Aplica lo aprendido. Retoma el ejemplo inicial y responde a las preguntas:
“San Luis Potosí presentó un lunes 15 de enero de 1951 en el municipio de Moctezuma, una temperatura de 13 grados centígrados bajo cero. De acuerdo con datos de la CONAGUA, la temperatura mínima promedio en 2018 en los siguientes estados fue de: Nuevo León -3ºC y Tamaulipas -4ºC:”
¿Cuál es la diferencia entre las temperaturas que se tienen registradas en el municipio de Moctezuma en San Luis Potosí y Tamaulipas?,
¿Cuál es la diferencia entre las temperaturas que se tienen registradas en el municipio de Moctezuma en San Luis Potosí y Nuevo León?
¿Qué significan estas diferencias?
Para responder la primera pregunta, plantea la siguiente sustracción: (− 13) – (−4), donde -13 representa temperatura de 13 grados centígrados bajo cero y –4 la temperatura de -4 grados centígrados bajo cero.
Ahora aplica la regla: Restar un número, positivo o negativo es lo mismo que sumar por su opuesto:
Por lo que se tiene: (−13) + (+4)=−9
Al resolver la sustracción, identificamos que la diferencia de temperaturas es de -9ºC. Pero, ¿qué significado tiene este resultado? Esto significa que, de -13ºC a menos 4 grados centígrados hay menos 9 grados.
Para responder la segunda pregunta, plantea la siguiente sustracción: (− 13) – (−3), donde -13 representa temperatura de 13 grados centígrados bajo cero y –4 la temperatura de -4 grados centígrados bajo cero.
Ahora aplicamos la regla: Restar un número, positivo o negativo es lo mismo que sumar por su opuesto:
Por lo que se tiene: (−13) + (+3) =−10
Al resolver la sustracción, identificamos que la diferencia de temperaturas es de -10ºC. Pero, ¿qué significado tiene este resultado? Esto significa que, de -13ºC a menos 4 grados centígrados hay menos 9 grados.
RESUMEN:Analiza la siguiente pregunta:
¿Cómo surgen estas operaciones con números enteros?
Para llegar a desarrollar estructuras aditivas con números enteros, las matemáticas han tenido que recorrer un largo camino. En el siglo III antes de nuestra era, los chinos trabajaron con cantidades negativas. Para ello, utilizaron dos conjuntos de varillas, unas rojas para las positivas y otras negras para las negativas.
Tuvieron que pasar todavía unos mil años, hasta que en el siglo VII, en India, se sistematizó el uso de los números negativos, del cero y de la regla de los signos. Desde la India, y gracias a los árabes, estos conceptos llegaron a Europa hacia el siglo IX. Sin embargo, hasta el siglo XV no aparecieron los signos positivos y negativos, primero, para designar cantidades positivas y negativas, y después, para las operaciones de suma y resta. El signo igual (=) se inventó en 1560.
En la actualidad, lo que tú puedes escribir en unos instantes, a distintos estudiosos de la ciencia de la matemática les costó miles de años.
Observa el siguiente ejemplo de operación con números enteros ya sean positivos o negativos según sea el caso:
Ejemplo, operación con números enteros positivos o negativos:
“Carlos tenía 20 pesos en su alcancía, posteriormente ahorró 50 pesos más; al paso de unos días decidió sacar 60 pesos de la alcancía para hacer una compra y por último, pudo ahorrar 30 pesos más.”
¿Cuánto dinero tiene en la alcancía? ¿Qué procedimiento u operación puedes establecer para responder la pregunta?
Para dar respuesta tendrás que construir una operación con números enteros, en los que los números positivos representan los ahorros de Carlos y los números negativos, el dinero que sacó de la alcancía.
Para dar solución a la situación usa la siguiente tabla, en donde se registran las cantidades que representan el ahorro y los gastos de Carlos.

En la primera columna de la tabla se registra la cantidad del dinero que ahorró con números positivos: 20, 50 y 30 pesos, y en la segunda columna, la cantidad de dinero que gastó para hacer su compra: 60 pesos, que representamos con números negativos por ser un egreso.
Se suman los números positivos: 20 más 50 más 30 que es igual a 100, posteriormente realizamos la adición entre números positivos y negativos, 100 positivo más 60 negativo es igual a 40 positivo.
Por lo tanto, la alcancía contiene 40 pesos.
Lo anterior puedes representarlo en una recta numérica, con una suma; los números positivos representan movimientos a la derecha y los negativos, movimientos a la izquierda. Ubica el cero y se hacen movimientos de 100 unidades a la derecha, que es el dinero que ahorró Carlos, llegando al 100 positivo, después, se hace el movimiento de 60 unidades a la izquierda, para representar los 60 negativos que se suman a 100, llegando al número 40 positivo. Tal como lo muestra la siguiente imagen:

La regla de la adición de números positivos y negativos dice que: al sumar números que tienen signo diferente, se calcula la diferencia entre sus valores absolutos y el resultado conserva el signo del número con mayor valor absoluto.
Analiza la siguiente pregunta:
¿En qué situación dentro de tu vida diaria podrías ejemplificar el uso de números negativos y positivos?
Observa a siguiente imagen:

En la imagen observas el recibo de Leslie en el que se incluye el resumen de movimientos. Cabe aclarar que las cantidades muestran las ganancias y pérdidas que obtiene la compañía telefónica con los consumos mensuales. El resumen de ganancias y pérdidas es el siguiente:
La compañía cobra por el servicio 250 pesos, por datos de internet 50 pesos; por mensajes, 25 pesos; consulta a buzón de voz, 18 pesos.
Pero descontaron por bonificación del equipo 101 pesos; 64 pesos por una falla de sistema y 33 pesos por una promoción de llamadas, estas cantidades se representan con números negativos por ser pérdidas para la compañía.
También cobraron un enlace de llamadas internacionales de 22 pesos; por un excedente de llamadas mensuales, 78 pesos; por un excedente por datos mensuales, 123 pesos, y por último, hicieron una bonificación por ser cliente preferencial de 33 pesos. El total del cobro es de 565 pesos.
A partir de lo planteado, piensa en la siguiente pregunta:
¿Qué tienes que realizar para determinar si el cobro fue correcto?
Te propongo organizar la información en una tabla, en una columna registra los conceptos que generan ganancias a la compañía, es decir, los cobros y en la segunda columna, los reembolsos o descuentos por promociones. Tal como lo muestra la siguiente imagen:
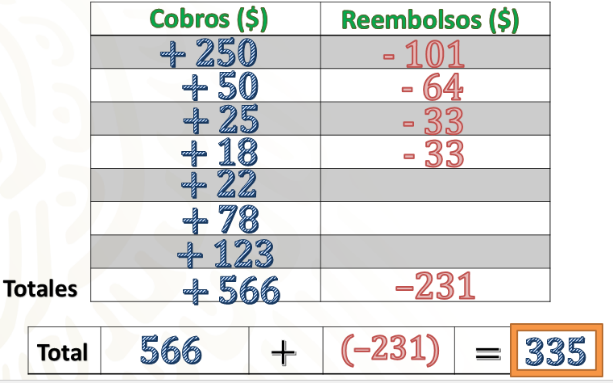
La primera columna muestra los cobros y la segunda, los rembolsos. Sumaremos las cantidades de las columnas por separado para obtener los totales de positivos y negativos, para posteriormente adicionarlos. Se sabe que al sumar números positivos o números negativos, se suman los valores absolutos y el resultado conserva el signo de los números en cuestión.
En la primera columna la suma de 250 más 50 más 25 más 18 más 22 más 78 más 123 es igual a 566 positivo. En la segunda columna: 101 negativo más 64 negativo más 33 negativo más 33 negativo es igual a 231 negativo.
Ahora suma 566 más 231 negativo, para ello calculamos la diferencia entre los valores absolutos 566 menos 231 es igual a 335 y como el valor absoluto de 566 positivo es mayor que el de 231 negativo, entonces 566 más 231 negativo es igual a 335 positivo.
Por lo tanto el cobro que tuvieron que hacerle a Leslie es de 335 pesos. Como puedes ver, el cobro del servicio debió ser menor al que señala el recibo.
Observa la siguiente situación para aplicar el uso de la adición de números positivos y negativos
“En Chihuahua, cierto día de invierno, a las 7 de la mañana la temperatura era de dos grados bajo cero. A las doce del mediodía, la temperatura había subido 8 grados, a las dos de la tarde subió 3 grados más. De las dos de la tarde a las ocho de la noche la temperatura descendió 5 grados y, para la medianoche bajó 6 grados más.”
¿Cuál era la temperatura a la media noche?
¿Cómo representarías las temperaturas que ascienden y descienden?
Para darle solución a la situación observa la siguiente imagen.
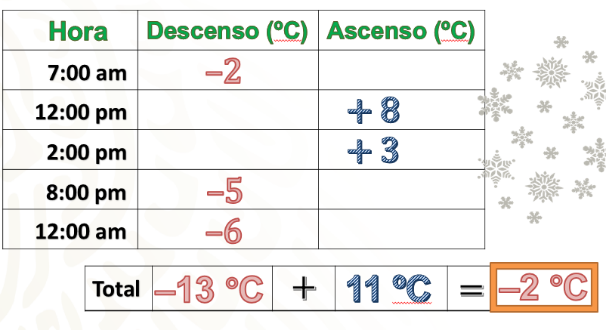
Escribe en una tabla en la primera columna, la hora en la que se registró la variación de la temperatura, en la segunda columna, el registro de las temperaturas que descendieron y en la tercera columna el registro de las temperaturas que ascendieron.
A las 7 de la mañana la temperatura era de dos grados bajo cero, a las 12 del día aumentó 8 grados; para las 2 de tarde aumentó 3 grados más; a las 8 de la noche descendió 5 grados y para la media noche descendió 6 grados más. Sumamos las temperaturas que descendieron y obtuvimos 13 grados negativos y las temperaturas que ascendieron suman 11 grados, aplicando la regla de la suma de números positivos y negativos, se calcula la diferencia entre los valores absolutos, por lo cual obtenemos 2 y como la cantidad con mayor valor absoluto, es negativa, por lo tanto, la temperatura a la media noche era de 2 grados Celsius negativos, es decir, 2 grados bajo cero.
Al sumar dos números positivos o números negativos, se suman los valores absolutos y el resultado conserva el signo de los números en cuestión.
Al sumar un número positivo y uno negativo, se calcula la diferencia entre los valores absolutos y el resultado conserva el signo del número con mayor valor absoluto.
Observa el siguiente ejemplo sobre la manera de sustraer números positivos y negativos:
“La hermana de Leslie tiene una tarjeta de crédito, y en su último estado de cuenta llegaron tres cargos; uno por 450 pesos, un segundo por 520 y otro por 380 pesos, como pueden ver en su pantalla. Al revisar ella no reconoció el gasto de 450 pesos y fue al banco a hacer la aclaración. El banco acepto el error y le descontaron ese dinero de su deuda.”
De acuerdo con la información de la tabla,
¿Cuál era la deuda de la hermana de Leslie? ¿Cuál fue su deuda después de la aclaración? ¿Cuáles operaciones de números positivos y negativos permiten responder las preguntas anteriores?
Profesor, para responder a la pregunta: ¿cuál era la deuda de la hermana de Leslie? Tienes que realizar una suma de números negativos: 450 negativo, más 520 negativo más 380 negativo.
Al resolver la suma de los números negativos el resultado es igual a 1,350 negativo, es decir, la deuda de mi hermana era de 1,350 pesos.
En el caso de la pregunta, ¿cuál fue su deuda después de la aclaración? Tienes dos palabras clave, descontar, palabra relaciona con una sustracción y deuda que se relaciona con números negativos, analicemos la siguiente explicación.
A la deuda de 1,350 pesos negativos se le tiene que descontar 450 pesos negativos de la aclaración. La operación que resulta es una sustracción de un número negativo menos un número negativo, como pueden ver: 1,350 negativo, menos 450 negativo.
Al representar la situación en la recta numérica nos movemos a la derecha, porque si lo hacemos a la izquierda estaríamos sumando un número negativo, agregando una deuda, como lo vimos en la adición y ahora lo que hacemos es restar o descontar una deuda. Entonces, al movernos 450 unidades a la derecha llegamos al número 900 negativo. Lo que significa que la deuda de mi hermana quedó en 900 pesos después de la aclaración.
Aplica lo aprendido. Retoma el ejemplo inicial y responde a las preguntas:
“San Luis Potosí presentó un lunes 15 de enero de 1951 en el municipio de Moctezuma, una temperatura de 13 grados centígrados bajo cero. De acuerdo con datos de la CONAGUA, la temperatura mínima promedio en 2018 en los siguientes estados fue de: Nuevo León -3ºC y Tamaulipas -4ºC:”
¿Cuál es la diferencia entre las temperaturas que se tienen registradas en el municipio de Moctezuma en San Luis Potosí y Tamaulipas?,
¿Cuál es la diferencia entre las temperaturas que se tienen registradas en el municipio de Moctezuma en San Luis Potosí y Nuevo León?
¿Qué significan estas diferencias?
Para responder la primera pregunta, plantea la siguiente sustracción: (− 13) – (−4), donde -13 representa temperatura de 13 grados centígrados bajo cero y –4 la temperatura de -4 grados centígrados bajo cero.
Ahora aplica la regla: Restar un número, positivo o negativo es lo mismo que sumar por su opuesto:
Por lo que se tiene: (−13) + (+4)=−9
Al resolver la sustracción, identificamos que la diferencia de temperaturas es de -9ºC. Pero, ¿qué significado tiene este resultado? Esto significa que, de -13ºC a menos 4 grados centígrados hay menos 9 grados.
Para responder la segunda pregunta, plantea la siguiente sustracción: (− 13) – (−3), donde -13 representa temperatura de 13 grados centígrados bajo cero y –4 la temperatura de -4 grados centígrados bajo cero.
Ahora aplicamos la regla: Restar un número, positivo o negativo es lo mismo que sumar por su opuesto:
Por lo que se tiene: (−13) + (+3) =−10
Al resolver la sustracción, identificamos que la diferencia de temperaturas es de -10ºC. Pero, ¿qué significado tiene este resultado? Esto significa que, de -13ºC a menos 4 grados centígrados hay menos 9 grados.
Analiza la siguiente pregunta:
¿Cómo surgen estas operaciones con números enteros?
Para llegar a desarrollar estructuras aditivas con números enteros, las matemáticas han tenido que recorrer un largo camino. En el siglo III antes de nuestra era, los chinos trabajaron con cantidades negativas. Para ello, utilizaron dos conjuntos de varillas, unas rojas para las positivas y otras negras para las negativas.
Tuvieron que pasar todavía unos mil años, hasta que en el siglo VII, en India, se sistematizó el uso de los números negativos, del cero y de la regla de los signos. Desde la India, y gracias a los árabes, estos conceptos llegaron a Europa hacia el siglo IX. Sin embargo, hasta el siglo XV no aparecieron los signos positivos y negativos, primero, para designar cantidades positivas y negativas, y después, para las operaciones de suma y resta. El signo igual (=) se inventó en 1560.
En la actualidad, lo que tú puedes escribir en unos instantes, a distintos estudiosos de la ciencia de la matemática les costó miles de años.
Observa el siguiente ejemplo de operación con números enteros ya sean positivos o negativos según sea el caso:
Ejemplo, operación con números enteros positivos o negativos:
“Carlos tenía 20 pesos en su alcancía, posteriormente ahorró 50 pesos más; al paso de unos días decidió sacar 60 pesos de la alcancía para hacer una compra y por último, pudo ahorrar 30 pesos más.”
¿Cuánto dinero tiene en la alcancía? ¿Qué procedimiento u operación puedes establecer para responder la pregunta?
Para dar respuesta tendrás que construir una operación con números enteros, en los que los números positivos representan los ahorros de Carlos y los números negativos, el dinero que sacó de la alcancía.
Para dar solución a la situación usa la siguiente tabla, en donde se registran las cantidades que representan el ahorro y los gastos de Carlos.

En la primera columna de la tabla se registra la cantidad del dinero que ahorró con números positivos: 20, 50 y 30 pesos, y en la segunda columna, la cantidad de dinero que gastó para hacer su compra: 60 pesos, que representamos con números negativos por ser un egreso.
Se suman los números positivos: 20 más 50 más 30 que es igual a 100, posteriormente realizamos la adición entre números positivos y negativos, 100 positivo más 60 negativo es igual a 40 positivo.
Por lo tanto, la alcancía contiene 40 pesos.
Lo anterior puedes representarlo en una recta numérica, con una suma; los números positivos representan movimientos a la derecha y los negativos, movimientos a la izquierda. Ubica el cero y se hacen movimientos de 100 unidades a la derecha, que es el dinero que ahorró Carlos, llegando al 100 positivo, después, se hace el movimiento de 60 unidades a la izquierda, para representar los 60 negativos que se suman a 100, llegando al número 40 positivo. Tal como lo muestra la siguiente imagen:

La regla de la adición de números positivos y negativos dice que: al sumar números que tienen signo diferente, se calcula la diferencia entre sus valores absolutos y el resultado conserva el signo del número con mayor valor absoluto.
Analiza la siguiente pregunta:
¿En qué situación dentro de tu vida diaria podrías ejemplificar el uso de números negativos y positivos?
Observa a siguiente imagen:

En la imagen observas el recibo de Leslie en el que se incluye el resumen de movimientos. Cabe aclarar que las cantidades muestran las ganancias y pérdidas que obtiene la compañía telefónica con los consumos mensuales. El resumen de ganancias y pérdidas es el siguiente:
La compañía cobra por el servicio 250 pesos, por datos de internet 50 pesos; por mensajes, 25 pesos; consulta a buzón de voz, 18 pesos.
Pero descontaron por bonificación del equipo 101 pesos; 64 pesos por una falla de sistema y 33 pesos por una promoción de llamadas, estas cantidades se representan con números negativos por ser pérdidas para la compañía.
También cobraron un enlace de llamadas internacionales de 22 pesos; por un excedente de llamadas mensuales, 78 pesos; por un excedente por datos mensuales, 123 pesos, y por último, hicieron una bonificación por ser cliente preferencial de 33 pesos. El total del cobro es de 565 pesos.
A partir de lo planteado, piensa en la siguiente pregunta:
¿Qué tienes que realizar para determinar si el cobro fue correcto?
Te propongo organizar la información en una tabla, en una columna registra los conceptos que generan ganancias a la compañía, es decir, los cobros y en la segunda columna, los reembolsos o descuentos por promociones. Tal como lo muestra la siguiente imagen:

La primera columna muestra los cobros y la segunda, los rembolsos. Sumaremos las cantidades de las columnas por separado para obtener los totales de positivos y negativos, para posteriormente adicionarlos. Se sabe que al sumar números positivos o números negativos, se suman los valores absolutos y el resultado conserva el signo de los números en cuestión.
En la primera columna la suma de 250 más 50 más 25 más 18 más 22 más 78 más 123 es igual a 566 positivo. En la segunda columna: 101 negativo más 64 negativo más 33 negativo más 33 negativo es igual a 231 negativo.
Ahora suma 566 más 231 negativo, para ello calculamos la diferencia entre los valores absolutos 566 menos 231 es igual a 335 y como el valor absoluto de 566 positivo es mayor que el de 231 negativo, entonces 566 más 231 negativo es igual a 335 positivo.
Por lo tanto el cobro que tuvieron que hacerle a Leslie es de 335 pesos. Como puedes ver, el cobro del servicio debió ser menor al que señala el recibo.
Observa la siguiente situación para aplicar el uso de la adición de números positivos y negativos
“En Chihuahua, cierto día de invierno, a las 7 de la mañana la temperatura era de dos grados bajo cero. A las doce del mediodía, la temperatura había subido 8 grados, a las dos de la tarde subió 3 grados más. De las dos de la tarde a las ocho de la noche la temperatura descendió 5 grados y, para la medianoche bajó 6 grados más.”
¿Cuál era la temperatura a la media noche?
¿Cómo representarías las temperaturas que ascienden y descienden?
Para darle solución a la situación observa la siguiente imagen.

Escribe en una tabla en la primera columna, la hora en la que se registró la variación de la temperatura, en la segunda columna, el registro de las temperaturas que descendieron y en la tercera columna el registro de las temperaturas que ascendieron.
A las 7 de la mañana la temperatura era de dos grados bajo cero, a las 12 del día aumentó 8 grados; para las 2 de tarde aumentó 3 grados más; a las 8 de la noche descendió 5 grados y para la media noche descendió 6 grados más. Sumamos las temperaturas que descendieron y obtuvimos 13 grados negativos y las temperaturas que ascendieron suman 11 grados, aplicando la regla de la suma de números positivos y negativos, se calcula la diferencia entre los valores absolutos, por lo cual obtenemos 2 y como la cantidad con mayor valor absoluto, es negativa, por lo tanto, la temperatura a la media noche era de 2 grados Celsius negativos, es decir, 2 grados bajo cero.
Al sumar dos números positivos o números negativos, se suman los valores absolutos y el resultado conserva el signo de los números en cuestión.
Al sumar un número positivo y uno negativo, se calcula la diferencia entre los valores absolutos y el resultado conserva el signo del número con mayor valor absoluto.
Observa el siguiente ejemplo sobre la manera de sustraer números positivos y negativos:
“La hermana de Leslie tiene una tarjeta de crédito, y en su último estado de cuenta llegaron tres cargos; uno por 450 pesos, un segundo por 520 y otro por 380 pesos, como pueden ver en su pantalla. Al revisar ella no reconoció el gasto de 450 pesos y fue al banco a hacer la aclaración. El banco acepto el error y le descontaron ese dinero de su deuda.”
De acuerdo con la información de la tabla,
¿Cuál era la deuda de la hermana de Leslie? ¿Cuál fue su deuda después de la aclaración? ¿Cuáles operaciones de números positivos y negativos permiten responder las preguntas anteriores?
Profesor, para responder a la pregunta: ¿cuál era la deuda de la hermana de Leslie? Tienes que realizar una suma de números negativos: 450 negativo, más 520 negativo más 380 negativo.
Al resolver la suma de los números negativos el resultado es igual a 1,350 negativo, es decir, la deuda de mi hermana era de 1,350 pesos.
En el caso de la pregunta, ¿cuál fue su deuda después de la aclaración? Tienes dos palabras clave, descontar, palabra relaciona con una sustracción y deuda que se relaciona con números negativos, analicemos la siguiente explicación.
A la deuda de 1,350 pesos negativos se le tiene que descontar 450 pesos negativos de la aclaración. La operación que resulta es una sustracción de un número negativo menos un número negativo, como pueden ver: 1,350 negativo, menos 450 negativo.
Al representar la situación en la recta numérica nos movemos a la derecha, porque si lo hacemos a la izquierda estaríamos sumando un número negativo, agregando una deuda, como lo vimos en la adición y ahora lo que hacemos es restar o descontar una deuda. Entonces, al movernos 450 unidades a la derecha llegamos al número 900 negativo. Lo que significa que la deuda de mi hermana quedó en 900 pesos después de la aclaración.