MATEMÁTICAS - SECUNDARIA 1
Representaciones equivalentes entre fracciones y decimales I
(JUEVES 14 ENERO)
ACTIVIDAD:Anota en tu cuaderno las siguientes fracciones e identifica haciendo los cálculos correspondientes, aquellas fracciones que tienen una fracción decimal equivalente y cuáles tienen como representación una expansión decimal o un número periódico.

RESUMEN:
Las matemáticas están presentes en diversas situaciones de la vida cotidiana y son útiles en aspectos tanto elementales como de gran complejidad en campos científicos y tecnológicos. De hecho, guardan una estrecha relación con ciencias como la física y la química, entre otras.
Con relación a lo descrito anteriormente, escribe en tu cuaderno las asignaturas o áreas del conocimiento, en las que consideras que las matemáticas se encuentran presentes y que pueden utilizarse, tal vez puedes describir algunos ejemplos de cómo se da esta vinculación.
En esta lección se emplearán algunos ejemplos sobre conocimientos matemáticos que son útiles en algunos campos científicos y tecnológicos, específicamente las representaciones equivalentes entre fracciones y decimales.
Por ejemplo: en tecnología usan las matemáticas, específicamente usan las fracciones para medir y hacer cálculos para la creación de proyectos técnicos.
A partir de los saberes previos que tienes, ¿cómo se escribe una fracción?
La fracción está compuesta por un numerador y un denominador, a partir de la cual se puede obtener su equivalencia decimal, al realizar una división. Si se divide el numerador entre el denominador, el resultado, es decir, el cociente de la división, es una equivalencia de la fracción y puede estar compuesta por números enteros o decimales.
Pero, ¿qué se entiende por equivalencia en este contexto?
Es una pregunta importante, ya que tener claridad de lo que es una equivalencia, es de gran utilidad en matemáticas. Para contestar la pregunta, se usará un ejemplo:
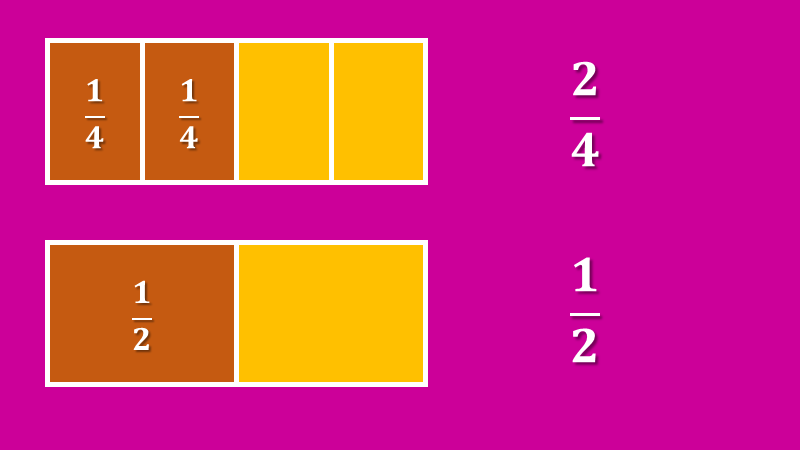
La fracción dos cuartos es equivalente a la fracción un medio. Como se observa en la imagen, el área sombreada en color naranja es la misma para ambas fracciones. Así, dos cuartos, equivale a un medio, y esto se puede comprobar si se divide el numerador entre el denominador, primero en una fracción y luego en otra.
¿Qué resultado esperarías obtener en cada caso?
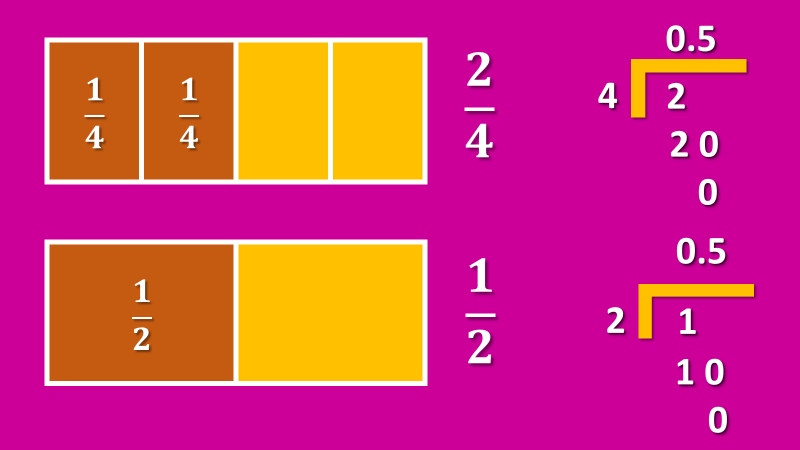
La respuesta, es que el cociente de ambas divisiones debe ser el mismo porque las fracciones son equivalentes. Así es. Si se divide dos entre cuatro el resultado es igual a cinco décimos, de igual manera, al dividir uno entre dos el resultado también es cinco décimos.
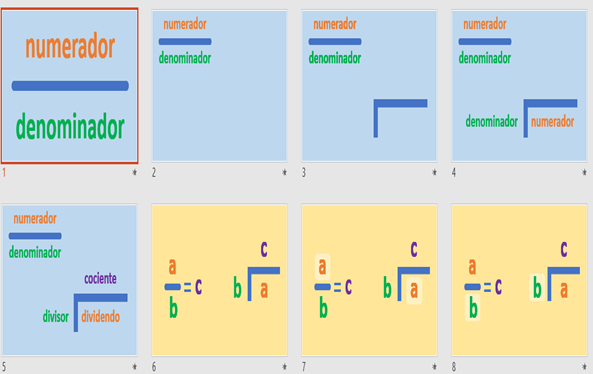
Una fracción puede tener distintos significados: puede representar la parte o partes de un todo, o representar una razón entre dos cantidades o también puede representar un cociente.
Es decir, expresa una división en la que, el numerador es el dividendo y el denominador es el divisor. Cuando se escribe la fracción “a” sobre “b”, donde “a” es el numerador y “b” es el denominador, existe implícita la equivalencia “a” entre “b” igual a “c”, donde “a” es el dividendo y “b” es el divisor y “c” representa el cociente.
Ahora, revisa algunas observaciones sobre los diferentes tipos de fracciones:
Una fracción propia es aquella en la que el numerador es menor al denominador, por ejemplo: dos quintos. Si se procede a realizar la división, 2 entre 5, el cociente es 0.4 que es un número decimal. El cociente de una fracción propia siempre resultará un número decimal menor a la unidad.
Por otro lado, una fracción impropia es aquella en la que el numerador es mayor o igual que el denominador.
Analiza dos ejemplos; primero, quince medios. Para encontrar el cociente se escribe la división 15 entre 2. Al realizar la operación se encuentra que el resultado es 7.5. Es posible afirmar que el cociente es una fracción impropia, por lo que resultará un número igual o mayor a la unidad.
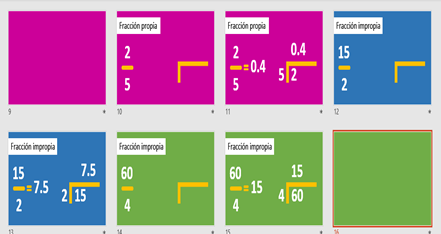
Cabe señalar que, en las fracciones impropias, no siempre se obtendrá un cociente que sea un número con una parte decimal, puede ser un número entero sin decimales. Lo que lleva a un segundo ejemplo de una fracción impropia, analiza: sesenta cuartos. Si realizas la operación, el cociente es 15, que es un número entero. Independientemente si el cociente resulta un número entero o decimal, al cociente de la división del numerador entre el denominador se le llama equivalencia o expansión decimal de la fracción.
A partir de estas observaciones, se puede afirmar que cuando se trata de un número mixto la equivalencia decimal de la fracción nunca será un número entero. Siempre será un número decimal.
Esta es una buena observación. Porque un número mixto se compone de un número entero más una fracción propia, así, a la parte entera se le sumará el cociente de la fracción propia que siempre es un número decimal. Por ejemplo: el número mixto 2 enteros un cuarto, tiene como equivalencia decimal dos enteros veinticinco centésimos, dado que la equivalencia decimal de la fracción propia un cuarto es veinticinco centésimos que, al sumarla con la parte entera, que en este caso es 2, efectivamente resulta dos enteros veinticinco centésimos.
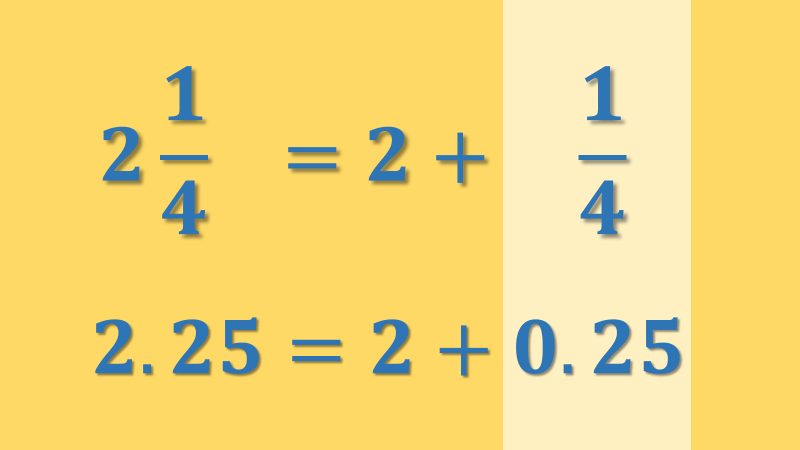
Dos expresiones matemáticas son equivalentes, cuando estas representan el mismo valor, aunque se escriban de forma diferente. Así también sucede con las fracciones.
Hay fracciones que son equivalentes entre sí, por ejemplo: sesenta cuartos es equivalente a quince medios. ¿Cómo demostrarías que son equivalentes?
Es importante destacar, que las fracciones tienen como ya se explicó una equivalencia o expansión decimal. Por ejemplo: cuatro quintos es equivalente a ocho décimos.
Para dar respuesta a la pregunta anteriormente planteada, se pude decir que obtener la equivalencia decimal de un número consiste en hallar el cociente del numerador entre el denominador de la fracción. En física y química puede ser útil encontrar la equivalencia decimal de una fracción. Por ejemplo, en el laboratorio de física es común utilizar la balanza para realizar experimentos. Una balanza es un instrumento de medición que permite conocer la masa de un cuerpo, que según el sistema internacional de unidades se mide en kilogramos.
Tal vez, hayas utilizado la balanza del laboratorio escolar en diferentes ocasiones, para medir la masa de un objeto. La balanza es un instrumento de medición útil en la vida cotidiana y también en el ámbito científico.
Revisa el siguiente ejemplo: en un laboratorio de física se comprobará que la masa de dos piezas de metal esté correctamente etiquetada, para lo cual es posible usar una balanza.
Para este ejemplo, la balanza es digital y su límite de medición es un kilogramo, por lo que en la pantalla aparece la medición en números decimales menores que uno.
Si la primera pieza de metal está etiquetada con una masa de un octavo de kilogramo, ¿qué valor decimal aparecerá en la pantalla de la balanza?
Para saber la medición en números decimales se puede obtener la equivalencia o expansión decimal de la fracción, un octavo.
Es correcto. Para obtener la equivalencia, el numerador 1 se divide entre el denominador 8.
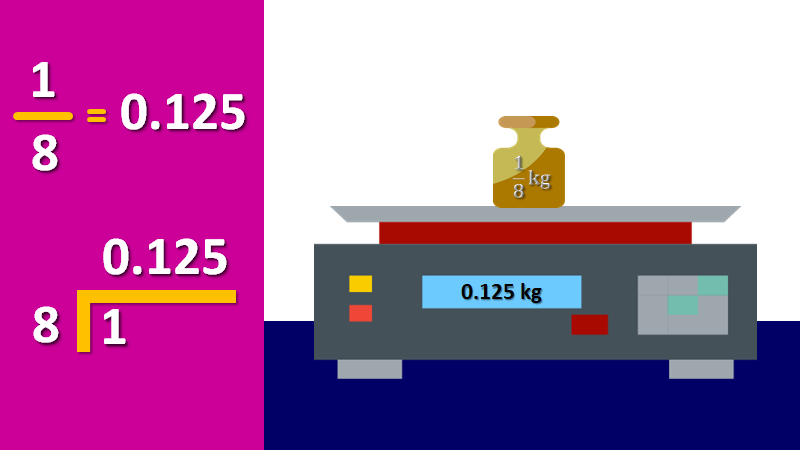
Como es una fracción propia se espera un cociente decimal y menor a uno. Al realizar la división, resulta ciento veinticinco milésimos, por lo que el uso de esta balanza es adecuado.
¿Por qué el número 0.125 se lee cómo ciento veinticinco milésimos?
Se lee así porque 0.125 llega hasta la tercera posición después del punto decimal, en donde se encuentran los milésimos, también es equivalente a una fracción decimal con denominador mil.
¡Es correcto!, pero tú, ¿qué entiendes por fracción decimal?
Registra tus ideas y puedes complementarlas con la siguiente información.
Una fracción decimal es aquella fracción en la que el denominador es una potencia del número 10, puede ser 10; 100; 1000; 10,000; 100,000, e.
En este caso el número 0.125 es equivalente a la fracción decimal 125 sobre 1000. Nota que, tanto el número decimal como la fracción se leen: ciento veinticinco milésimos. Por lo tanto, se puede afirmar que un octavo es equivalente a la fracción decimal 125 milésimos.
Qué tal si ahora escribes en tu cuaderno un par de ejemplos de fracciones decimales y cómo se leen.
Para ello se seguirá con el ejemplo.
La segunda pieza de metal está etiquetada con una masa de cuarenta y cinco centésimos de kilogramo.
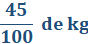
¿Qué valor decimal aparecerá en la pantalla de la balanza?
Para saber la medición en números decimales hay que encontrar la equivalencia o expansión decimal de la fracción cuarenta y cinco centésimos. Y encontrar la expansión o equivalencia decimal de este tipo de fracciones puede hacerse sin necesidad de resolver la división escrita usando la galera, que es el nombre correcto de la “casita” de la división.
Sí, de hecho, se puede hacer de forma mental, sólo se tiene que escribir el numerador de la fracción y recorrer el punto decimal hacia la izquierda tantos ceros tenga el denominador. En este caso sería 0.45.
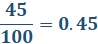
Así es, puedes hacer los cálculos de forma mental, dividiendo entre 10, 100 u otra potencia de 10.
Con base en este procedimiento, se explicará la forma de convertir números decimales en fracciones decimales.
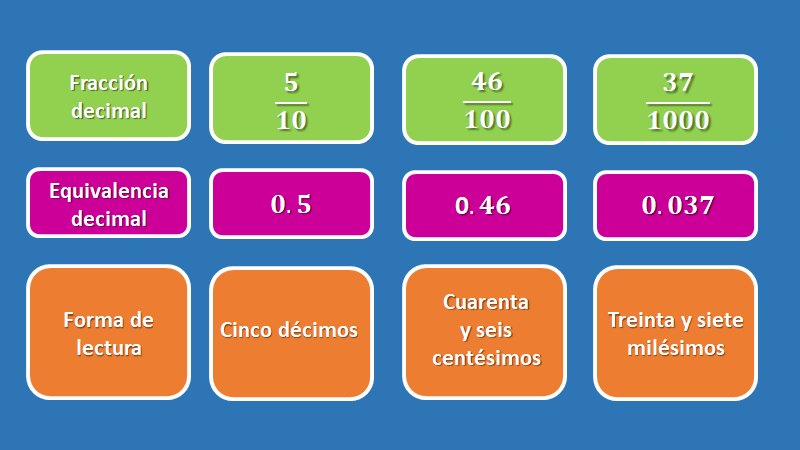
Como una fracción decimal tiene como denominador una potencia del número 10, por ejemplo: 5/10; 46/100; 37/1000.
Encontrar la expansión decimal de esas fracciones, implica dividir el numerador entre el denominador, que en cada uno de los casos es: 0.5; 0.46; 0.037.
También puede resultar sencillo si se lee de la siguiente forma: Cinco décimos, cuarenta y seis centésimos y treinta y siete milésimos.
De hecho, la lectura de los números decimales de esta manera es útil para convertir números decimales a una fracción.
Por ejemplo:
0.75 se lee como setenta y cinco centésimos, y se puede expresar como la fracción 75/100, que también se puede leer como setenta y cinco centésimos. Para comprobar, la expansión decimal de 75/100 resulta de dividir 75 entre 100, que efectivamente es 0.75.
Para convertir un número decimal a una fracción decimal equivalente es útil recorrer el punto decimal hacia la derecha hasta que quede un número entero. Si a 0.75 se le recorre el punto decimal hacia la derecha para que quede un número entero, se debe recorrer dos posiciones, así el entero resultante es 75. Éste será el numerador de la fracción.
Y el denominador número resultante de multiplicar por sí mismo al 10, tantas veces como el número de posiciones recorridas, para el ejemplo es 2, así que el denominador será 10 x 10 = 100. Por eso, una fracción equivalente de 0.75 es 75/100, aunque esta fracción se puede simplificar a 15/20, y más aún puede simplificarse a 3/4. Es decir, la fracción propia 3/4 tiene como fracción decimal equivalente a la fracción 75/100.
Ahora, se convertirá el número 6.425 a una fracción decimal. Si se recorre el punto decimal hacia la derecha hasta lograr un número entero, se debe recorrer el punto tres posiciones, quedando 6425. Este número será el numerador.
El denominador se multiplica por sí mismo al 10, tantas veces como el número de posiciones recorridas, en este caso 3. Así que el denominador es el resultado de la multiplicación 10 x 10 x 10 = 1000.
Nota que la cantidad de ceros es la misma que las posiciones recorridas en el número anterior. Por lo tanto, la fracción equivalente es 6425/1000 aunque esta fracción se puede simplificar a 1285/200 y luego a 257/40.
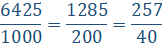
Bien a lo largo de esta sesión has estudiado cómo aplicar la equivalencia entre fracciones y números decimales. Ve el siguiente audiovisual a manera de resumen.
- 35. De fracción común a fracción decimal y viceversa.
Revisa del tiempo 01:39 al 4:00.
Después de revisar el video, te puede quedar más claro, por ejemplo, el número decimal 0.8 es equivalente a la fracción ocho décimos, es decir 8 sobre 10, que se puede simplificar como 4 sobre cinco o cuatro quintos.
Pero, ¿todas las fracciones tienen una fracción decimal equivalente?
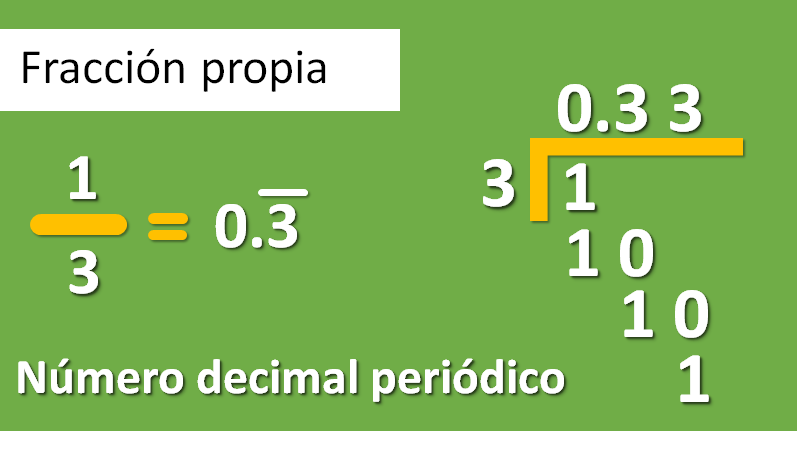
La respuesta es que hay fracciones que no tienen una representación o equivalencia como fracción decimal, ya que, al convertirlas a número decimal, el cociente es un número decimal periódico. Ve el siguiente caso, que es la fracción 1/3.
Al realizar la división para obtener el número decimal correspondiente, resulta 0.33 y residuo 1, si se sigue operando, el número 3 en el cociente se repetirá de manera infinita, es decir, se obtiene un número decimal con expansión infinita. A este tipo de números decimales se les conoce como número decimal periódico, eso significa que inmediatamente después del punto decimal hay una o más cifras que son repetitivas hasta el infinito y que para no omitir ninguna de las repeticiones se puede expresar como 0.3 con una testa, o segmento sobre el número que representa la periodicidad de la cifra.
Entonces, por ello, la fracción un tercio no tiene una representación equivalente como fracción decimal, porque su número decimal correspondiente únicamente es una aproximación, en este caso 0.3 periódico.
Has concluido la lección. Puedes solicitar a tu maestra o maestro a distancia que te pongan otras situaciones que contribuyan a dar sentido y significado a la conversión de números fraccionarios a decimales y viceversa.
Además, puedes consultar tu libro de Matemáticas de primer grado, ubica en él este tema. Resuelve todo lo que puedas para comprender el tema. Tal vez encuentres formas diferentes para realizar estos cálculos.
Anota en tu cuaderno las siguientes fracciones e identifica haciendo los cálculos correspondientes, aquellas fracciones que tienen una fracción decimal equivalente y cuáles tienen como representación una expansión decimal o un número periódico.

Las matemáticas están presentes en diversas situaciones de la vida cotidiana y son útiles en aspectos tanto elementales como de gran complejidad en campos científicos y tecnológicos. De hecho, guardan una estrecha relación con ciencias como la física y la química, entre otras.
Con relación a lo descrito anteriormente, escribe en tu cuaderno las asignaturas o áreas del conocimiento, en las que consideras que las matemáticas se encuentran presentes y que pueden utilizarse, tal vez puedes describir algunos ejemplos de cómo se da esta vinculación.
En esta lección se emplearán algunos ejemplos sobre conocimientos matemáticos que son útiles en algunos campos científicos y tecnológicos, específicamente las representaciones equivalentes entre fracciones y decimales.
Por ejemplo: en tecnología usan las matemáticas, específicamente usan las fracciones para medir y hacer cálculos para la creación de proyectos técnicos.
A partir de los saberes previos que tienes, ¿cómo se escribe una fracción?
La fracción está compuesta por un numerador y un denominador, a partir de la cual se puede obtener su equivalencia decimal, al realizar una división. Si se divide el numerador entre el denominador, el resultado, es decir, el cociente de la división, es una equivalencia de la fracción y puede estar compuesta por números enteros o decimales.
Pero, ¿qué se entiende por equivalencia en este contexto?
Es una pregunta importante, ya que tener claridad de lo que es una equivalencia, es de gran utilidad en matemáticas. Para contestar la pregunta, se usará un ejemplo:

La fracción dos cuartos es equivalente a la fracción un medio. Como se observa en la imagen, el área sombreada en color naranja es la misma para ambas fracciones. Así, dos cuartos, equivale a un medio, y esto se puede comprobar si se divide el numerador entre el denominador, primero en una fracción y luego en otra.
¿Qué resultado esperarías obtener en cada caso?
La respuesta, es que el cociente de ambas divisiones debe ser el mismo porque las fracciones son equivalentes. Así es. Si se divide dos entre cuatro el resultado es igual a cinco décimos, de igual manera, al dividir uno entre dos el resultado también es cinco décimos.

Una fracción puede tener distintos significados: puede representar la parte o partes de un todo, o representar una razón entre dos cantidades o también puede representar un cociente.
Es decir, expresa una división en la que, el numerador es el dividendo y el denominador es el divisor. Cuando se escribe la fracción “a” sobre “b”, donde “a” es el numerador y “b” es el denominador, existe implícita la equivalencia “a” entre “b” igual a “c”, donde “a” es el dividendo y “b” es el divisor y “c” representa el cociente.

Ahora, revisa algunas observaciones sobre los diferentes tipos de fracciones:
Una fracción propia es aquella en la que el numerador es menor al denominador, por ejemplo: dos quintos. Si se procede a realizar la división, 2 entre 5, el cociente es 0.4 que es un número decimal. El cociente de una fracción propia siempre resultará un número decimal menor a la unidad.
Por otro lado, una fracción impropia es aquella en la que el numerador es mayor o igual que el denominador.
Analiza dos ejemplos; primero, quince medios. Para encontrar el cociente se escribe la división 15 entre 2. Al realizar la operación se encuentra que el resultado es 7.5. Es posible afirmar que el cociente es una fracción impropia, por lo que resultará un número igual o mayor a la unidad.

Cabe señalar que, en las fracciones impropias, no siempre se obtendrá un cociente que sea un número con una parte decimal, puede ser un número entero sin decimales. Lo que lleva a un segundo ejemplo de una fracción impropia, analiza: sesenta cuartos. Si realizas la operación, el cociente es 15, que es un número entero. Independientemente si el cociente resulta un número entero o decimal, al cociente de la división del numerador entre el denominador se le llama equivalencia o expansión decimal de la fracción.
A partir de estas observaciones, se puede afirmar que cuando se trata de un número mixto la equivalencia decimal de la fracción nunca será un número entero. Siempre será un número decimal.
Esta es una buena observación. Porque un número mixto se compone de un número entero más una fracción propia, así, a la parte entera se le sumará el cociente de la fracción propia que siempre es un número decimal. Por ejemplo: el número mixto 2 enteros un cuarto, tiene como equivalencia decimal dos enteros veinticinco centésimos, dado que la equivalencia decimal de la fracción propia un cuarto es veinticinco centésimos que, al sumarla con la parte entera, que en este caso es 2, efectivamente resulta dos enteros veinticinco centésimos.
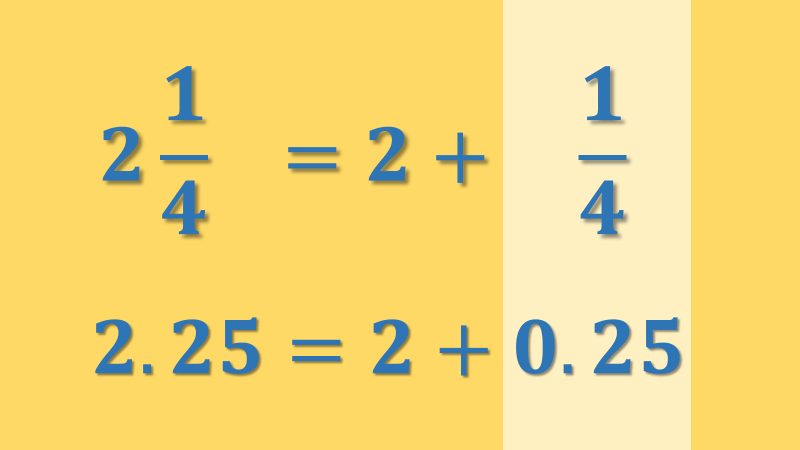
Dos expresiones matemáticas son equivalentes, cuando estas representan el mismo valor, aunque se escriban de forma diferente. Así también sucede con las fracciones.
Hay fracciones que son equivalentes entre sí, por ejemplo: sesenta cuartos es equivalente a quince medios. ¿Cómo demostrarías que son equivalentes?
Es importante destacar, que las fracciones tienen como ya se explicó una equivalencia o expansión decimal. Por ejemplo: cuatro quintos es equivalente a ocho décimos.
Para dar respuesta a la pregunta anteriormente planteada, se pude decir que obtener la equivalencia decimal de un número consiste en hallar el cociente del numerador entre el denominador de la fracción. En física y química puede ser útil encontrar la equivalencia decimal de una fracción. Por ejemplo, en el laboratorio de física es común utilizar la balanza para realizar experimentos. Una balanza es un instrumento de medición que permite conocer la masa de un cuerpo, que según el sistema internacional de unidades se mide en kilogramos.
Tal vez, hayas utilizado la balanza del laboratorio escolar en diferentes ocasiones, para medir la masa de un objeto. La balanza es un instrumento de medición útil en la vida cotidiana y también en el ámbito científico.
Revisa el siguiente ejemplo: en un laboratorio de física se comprobará que la masa de dos piezas de metal esté correctamente etiquetada, para lo cual es posible usar una balanza.
Para este ejemplo, la balanza es digital y su límite de medición es un kilogramo, por lo que en la pantalla aparece la medición en números decimales menores que uno.
Si la primera pieza de metal está etiquetada con una masa de un octavo de kilogramo, ¿qué valor decimal aparecerá en la pantalla de la balanza?
Para saber la medición en números decimales se puede obtener la equivalencia o expansión decimal de la fracción, un octavo.
Es correcto. Para obtener la equivalencia, el numerador 1 se divide entre el denominador 8.
Como es una fracción propia se espera un cociente decimal y menor a uno. Al realizar la división, resulta ciento veinticinco milésimos, por lo que el uso de esta balanza es adecuado.

¿Por qué el número 0.125 se lee cómo ciento veinticinco milésimos?
Se lee así porque 0.125 llega hasta la tercera posición después del punto decimal, en donde se encuentran los milésimos, también es equivalente a una fracción decimal con denominador mil.
¡Es correcto!, pero tú, ¿qué entiendes por fracción decimal?
Registra tus ideas y puedes complementarlas con la siguiente información.
Una fracción decimal es aquella fracción en la que el denominador es una potencia del número 10, puede ser 10; 100; 1000; 10,000; 100,000, e.
En este caso el número 0.125 es equivalente a la fracción decimal 125 sobre 1000. Nota que, tanto el número decimal como la fracción se leen: ciento veinticinco milésimos. Por lo tanto, se puede afirmar que un octavo es equivalente a la fracción decimal 125 milésimos.
Qué tal si ahora escribes en tu cuaderno un par de ejemplos de fracciones decimales y cómo se leen.
Para ello se seguirá con el ejemplo.
La segunda pieza de metal está etiquetada con una masa de cuarenta y cinco centésimos de kilogramo.
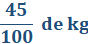
¿Qué valor decimal aparecerá en la pantalla de la balanza?
Para saber la medición en números decimales hay que encontrar la equivalencia o expansión decimal de la fracción cuarenta y cinco centésimos. Y encontrar la expansión o equivalencia decimal de este tipo de fracciones puede hacerse sin necesidad de resolver la división escrita usando la galera, que es el nombre correcto de la “casita” de la división.
Sí, de hecho, se puede hacer de forma mental, sólo se tiene que escribir el numerador de la fracción y recorrer el punto decimal hacia la izquierda tantos ceros tenga el denominador. En este caso sería 0.45.
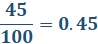
Así es, puedes hacer los cálculos de forma mental, dividiendo entre 10, 100 u otra potencia de 10.
Con base en este procedimiento, se explicará la forma de convertir números decimales en fracciones decimales.
Como una fracción decimal tiene como denominador una potencia del número 10, por ejemplo: 5/10; 46/100; 37/1000.
Encontrar la expansión decimal de esas fracciones, implica dividir el numerador entre el denominador, que en cada uno de los casos es: 0.5; 0.46; 0.037.
También puede resultar sencillo si se lee de la siguiente forma: Cinco décimos, cuarenta y seis centésimos y treinta y siete milésimos.

De hecho, la lectura de los números decimales de esta manera es útil para convertir números decimales a una fracción.
Por ejemplo:
0.75 se lee como setenta y cinco centésimos, y se puede expresar como la fracción 75/100, que también se puede leer como setenta y cinco centésimos. Para comprobar, la expansión decimal de 75/100 resulta de dividir 75 entre 100, que efectivamente es 0.75.
Para convertir un número decimal a una fracción decimal equivalente es útil recorrer el punto decimal hacia la derecha hasta que quede un número entero. Si a 0.75 se le recorre el punto decimal hacia la derecha para que quede un número entero, se debe recorrer dos posiciones, así el entero resultante es 75. Éste será el numerador de la fracción.
Y el denominador número resultante de multiplicar por sí mismo al 10, tantas veces como el número de posiciones recorridas, para el ejemplo es 2, así que el denominador será 10 x 10 = 100. Por eso, una fracción equivalente de 0.75 es 75/100, aunque esta fracción se puede simplificar a 15/20, y más aún puede simplificarse a 3/4. Es decir, la fracción propia 3/4 tiene como fracción decimal equivalente a la fracción 75/100.
Ahora, se convertirá el número 6.425 a una fracción decimal. Si se recorre el punto decimal hacia la derecha hasta lograr un número entero, se debe recorrer el punto tres posiciones, quedando 6425. Este número será el numerador.
El denominador se multiplica por sí mismo al 10, tantas veces como el número de posiciones recorridas, en este caso 3. Así que el denominador es el resultado de la multiplicación 10 x 10 x 10 = 1000.
Nota que la cantidad de ceros es la misma que las posiciones recorridas en el número anterior. Por lo tanto, la fracción equivalente es 6425/1000 aunque esta fracción se puede simplificar a 1285/200 y luego a 257/40.
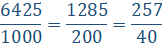
Bien a lo largo de esta sesión has estudiado cómo aplicar la equivalencia entre fracciones y números decimales. Ve el siguiente audiovisual a manera de resumen.
- 35. De fracción común a fracción decimal y viceversa.
Revisa del tiempo 01:39 al 4:00.
Después de revisar el video, te puede quedar más claro, por ejemplo, el número decimal 0.8 es equivalente a la fracción ocho décimos, es decir 8 sobre 10, que se puede simplificar como 4 sobre cinco o cuatro quintos.
Pero, ¿todas las fracciones tienen una fracción decimal equivalente?
La respuesta es que hay fracciones que no tienen una representación o equivalencia como fracción decimal, ya que, al convertirlas a número decimal, el cociente es un número decimal periódico. Ve el siguiente caso, que es la fracción 1/3.
Al realizar la división para obtener el número decimal correspondiente, resulta 0.33 y residuo 1, si se sigue operando, el número 3 en el cociente se repetirá de manera infinita, es decir, se obtiene un número decimal con expansión infinita. A este tipo de números decimales se les conoce como número decimal periódico, eso significa que inmediatamente después del punto decimal hay una o más cifras que son repetitivas hasta el infinito y que para no omitir ninguna de las repeticiones se puede expresar como 0.3 con una testa, o segmento sobre el número que representa la periodicidad de la cifra.

Entonces, por ello, la fracción un tercio no tiene una representación equivalente como fracción decimal, porque su número decimal correspondiente únicamente es una aproximación, en este caso 0.3 periódico.
Has concluido la lección. Puedes solicitar a tu maestra o maestro a distancia que te pongan otras situaciones que contribuyan a dar sentido y significado a la conversión de números fraccionarios a decimales y viceversa.
Además, puedes consultar tu libro de Matemáticas de primer grado, ubica en él este tema. Resuelve todo lo que puedas para comprender el tema. Tal vez encuentres formas diferentes para realizar estos cálculos.