SEC1-MAT-15ENE

 

MATEMÁTICAS  - SECUNDARIA 1

Representaciones equivalentes entre fracciones y decimales II

(VIERNES 15 ENERO)

ACTIVIDAD:

En tu libro de Matemáticas de primer grado, ubica este tema y resuelve todo lo que te sea posible para avanzar en el conocimiento sobre los números racionales.

RESUMEN:

Sabemos que te gusta mucho aprender; por eso te queremos compartir algunas curiosidades sobre una serie de números, y para eso nos gustaría que leyéras algunos párrafos de la sexta noche del libro, El diablo de los números.

 

El diablo de los números

Autor Hans Magnus Enzensberger

 

Un tipo simpático el viejo Bonatschi, fue uno de los primeros que entendieron el cero. Desde luego no lo inventó, pero en cambio se le ocurrió la idea de los números Bonatschi. ¡Deslumbrante! Como la mayoría de las buenas ideas, su invento empieza con el uno… ya sabes. Más exactamente con dos unos: 1 + 1 = 2.  Luego toma las dos últimas cifras y las suma: así que 1 + 2 = 3 y luego 2 + 3 = 5, otra vez 3 + 5 = 8, etcétera.

 

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…

 

Robert se tapó los oídos.

-Ya para- dijo el anciano. Quizá sea mejor que te los escriba para que puedas aprendértelos.

 

Desatornilló el extremo de su bastón y sacó un fino rollo de papel. Lo tiró al suelo y le dio un golpecito. ¡Es increíble la cantidad de papel que había dentro del bastón! Y naturalmente en el rollo estaba toda la serie de Bonatschi. A partir de ahí, los números estaban tan lejos y eran tan pequeños que Robert ya no pudo leerlos.

 

-Comprendo. Todo estupendo, pero dime para qué sirve.

-Oh, dijo el diablo de los números-, no te creas que las Matemáticas sólo son cosa de matemáticos. Incluso los árboles y los moluscos saben contar. El que aún no se crea que en la Naturaleza las cosas ocurren como si supieran contar, mire atentamente el árbol.

 

La lectura trata de una serie de números muy peculiar, que inicia con dos unos, y el sucesor del último uno se obtiene al sumarlos, es decir 1 + 1 = 2, y éste, al sumarlo con su antecesor, es decir, el 1 nos da como resultado 3… Así quedan 1, 1, 2, 3, 5, 8, 13, 21, 34…. etc. Aunque parece que son muchísimos números, como se menciona en el libro, en realidad no son tantos.

 

Esta serie sólo tiene números naturales, es decir, aquellos números que utilizamos para contar. Tomando en cuenta esta definición: ¿que número natural que se encuentra entre los dos primeros números de la serie?

 

Entre 1 y 1 no existe ningún otro número, ya que se refiere al mismo número; entre el segundo y tercer número de la serie que son 1 y 2 no existe ningún número natural; entre: 3 y 5 sí hay un sólo número natural entre ellos, aunque no forma parte de la serie, sabemos que entre el 3 y el 5 está el 4. ¿Piensas que entre dos números naturales consecutivos se pueden encontrar más números naturales?

 

Como acabas de analizar, entre dos números naturales consecutivos, por ejemplo, 2 y 3, 3 y 4, 4 y 5, etcétera, no existe ningún número natural. Sí existen otros números, como el 0.5 o 1/2, que se encuentra entre el cero y el uno, pero esos números ya no pertenecen al conjunto de números naturales, esos forman parte del conjunto de números racionales, es decir, todos los números que pueden representarse como el cociente de dos números enteros de la forma a/b, donde b es diferente de cero.

 

Realiza las siguientes actividades:

 

1. Luis corrió 2.4 km y Ana 2.5 km; Ema dice que corrió más que Luis, pero menos que Ana. ¿Es esto posible?, ¿habrá un número entre 2.4 y 2.5?, ¿qué distancia pudo recorrer Ana?

 

2. Al medir en una balanza un objeto con una pesa de 1/4 de kg, la masa del objeto fue mayor a esta medida y al usar dos pesas de 1/4, es decir, 2/4 de kg, la masa del objeto fue menor. María pensó que eso no era posible porque entre 1/4 y 2/4 no hay otra fracción. ¿Qué piensas?, ¿estás de acuerdo con María?

 

Observa el segmento que representa la distancia del kilómetro dos al tres, en él identificamos las distancias que recorrieron Luis 2.4 km y Ana 2.5 km. A ese segmento de 2.4 a 2.5 lo dividimos en diez partes iguales, así obtenemos 2.41, 2.42, 2.43, 2.44, 2.45, 2.46, 2.47, 2.48, y 2.49; siendo todos estos números las posibles distancias en kilómetros que pudo recorrer Ana.

 

 

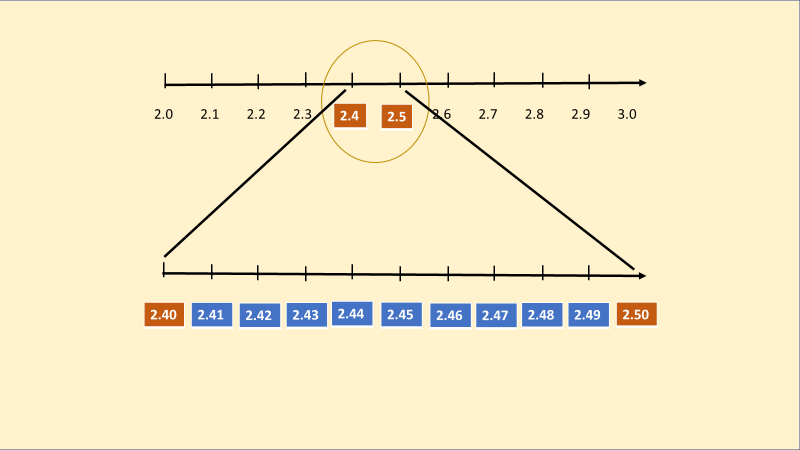
Aun cuando parecía que 2.4 y 2.5 eran números consecutivos, podemos observar que, a diferencia de los números naturales, en los decimales no existe un consecutivo, ya que entre dos números decimales siempre existirán infinidad de números. Respondiendo a las interrogantes, sí, es posible que Ema haya recorrido más que Luis y menos que Ana y una de las distancias que pudo recorrer fue, por ejemplo, 2.46 km.

 

Dividir el segmento en diez partes iguales nos permitió observar algunas posibles respuestas, pero no son las únicas, ya que ese segmento pudo dividirse en 100, 1000, 10000, y así podríamos seguir.

 

Revisemos ahora la segunda situación.

 

Representamos las pesas en un segmento de recta donde colocamos el cero y el uno en los extremos. Dividimos en cuatro partes iguales e identificamos las fracciones 1/4 y 2/4, que representan a las pesas que se usaron para medir la masa del objeto.

 

Después, en un segmento de recta, exactamente igual, dividimos, pero ahora en octavos, para encontrar las fracciones equivalentes a 1/4 y 2/4 con denominador 8, que son 2/8 y 4/8, respectivamente, así podemos observar que entre 1/4 y 2/4 encontramos la fracción 3/8.

 

 

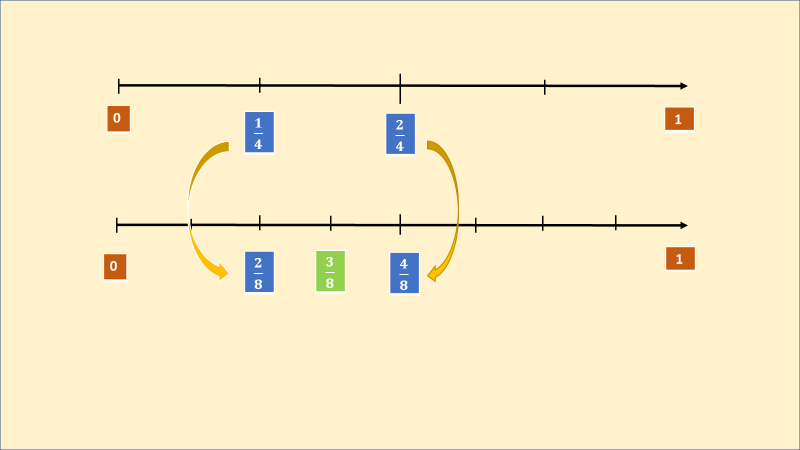
Respondiendo a la interrogante sabemos que María no tenía la razón, ya que pudimos encontrar la fracción 3/8, que al igual que sucedió con los decimales, no es la única, sabemos que existen más fracciones equivalentes a 1/4, por ejemplo 3/12, 4/16, 5/20, etcétera; y que entre mayor sea el denominador de la fracción equivalente, más fracciones podremos encontrar entre ¼ y 2/4.

 

Como puedes observar en los ejemplos anteriores de fracciones y decimales, en ellos, a diferencia de los naturales, sí podemos encontrar una infinidad de números, entre dos números dados y a eso se le conoce como propiedad de densidad.

 

Para entenderlo mejor, observa el siguiente video:

 

1. Densidad de los números decimales

https://youtu.be/V7eav3dtjnY

 

Los números son infinitos, pero debes tener presente que existen varios conjuntos de números, lo que es aún más interesante.

 

Una fracción representa las partes de un todo, al que llamamos unidad, es decir que ésta se divide en partes iguales y cada una de estas partes es una fracción del entero. Es importante tener en cuenta que, el entero es aquella medida que tomaras como referencia para la siguiente actividad.

 

En hojas de colores, o de rehúso, vas a marcar con el compás círculos de cualquier tamaño, te sugerimos que sean con un radio de 10.5 cm, para aprovechar al máximo las hojas. Si no tienes a la mano compás, puedes utilizar cualquier cosa con forma circular que tengas en casa para marcar los círculos.

 

Ahora vas a recortarlos, y cada uno de ellos lo dividirás en distintas cantidades; por ejemplo, en medios, tercios, cuartos, quintos, sextos, etcétera.

 

Algunas fracciones son fáciles de representar, como los medios, sólo debes doblar a la mitad el círculo, igual que con los cuartos tienes que doblar dos veces. Pero, ¿cómo le harías para marcar con los tercios?

 

Cuando el procedimiento de los dobleces no es el más adecuado, recurrimos al transportador. Sabemos que el círculo completo mide 360º, para marcar los tercios dividimos 360/3 = 120, y es la medida en grados que debe tener cada uno de los sectores circulares. Puedes marcar tantos círculos como sea posible. Una vez que tenemos marcados todos los círculos, vamos a doblarlos a la mitad y los pegaremos uno detrás del otro. Procurando que, un segmento de los que marcamos en cada círculo, quede en el mismo punto.

 

Con este círculo esperamos que quede más claro el concepto de entero y de fracciones. Puedes usarlo para saber qué fracciones se encuentran entre otras dos marcándolos por la mitad y pegándolos uno detrás de otro.

Por ejemplo: toma el círculo que representa los medios y el que representa los cuartos. Trabajaremos con las fracciones 1/4 y 1/2. Busca entre los demás círculos alguna fracción que se encuentre entre ellas. ¿Qué fracción puedes encontrar entre 14 y 12?

 

Es la fracción que corresponde a los octavos. El espacio corresponde a la fracción 3/8, por lo tanto entre 1/4 y 1/2 encontramos la fracción 3/8.

 

Identifica alguna fracción que se encuentre entre las fracciones 2/5 y 7/8.

 

El espacio corresponde a la fracción 7/10, por lo tanto podemos afirmar que entre las fracciones 2/5 y 7/8 una de las fracciones que se encuentran es 7/10

 

Retomando el concepto de que hay varias fracciones entre otras dos fracciones, considera que a eso se le conoce como propiedad de densidad. Ahora analiza algunos ejemplos, pero con decimales.

 

Analiza los siguiente pares de números y encuentra qué números hay entre ellos.

 

El primer par de números. 2 y 3

 

Imagina un segmento de recta entre el 2 y el 3, la dividimos en 10 partes iguales y encontramos los números 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9. Tomamos como ejemplo el 2.5, pero podemos observar que hay varios más.

 

 

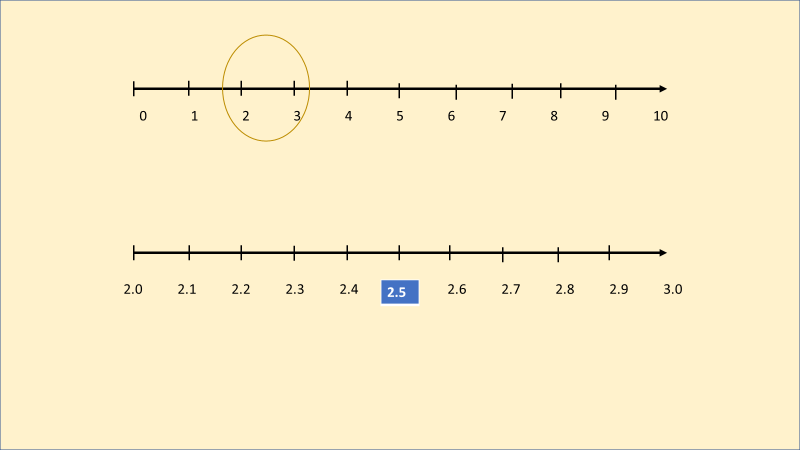
Es posible que hayas utilizado otro procedimiento para el cálculo, o que hayas pensado en otro número, ya que puedes observar que existen muchos más.

 

Vamos con otro par de números:  3.5 y 3.6.

 

 

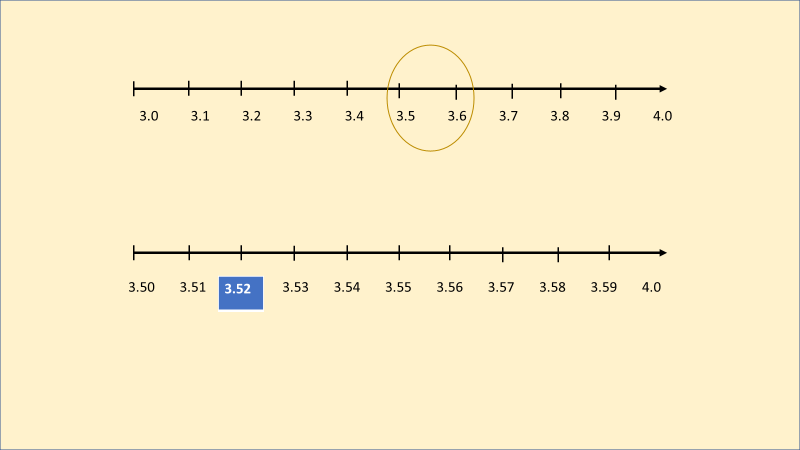
Ubicamos en la recta los números 3.5 y 3.6, ahora dividiremos ese segmento en diez partes iguales, así obtenemos 3.51, 3.52, 3.53, 3.54, 3.55, 3.56, 3.57, 3.58, 3.59. Y encontramos por ejemplo el 3.52.

 

Ahora, ¿un número entre 0.234 y 0.235?

 

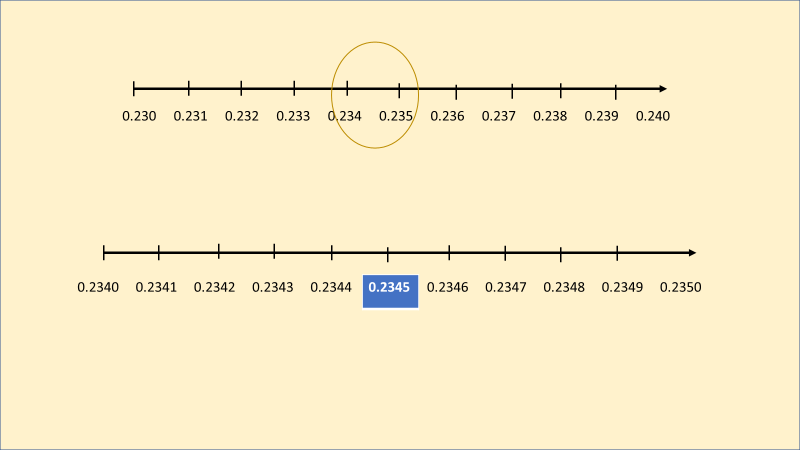
Siempre es posible encontrar un número decimal, entre dos decimales, siguiendo el procedimiento anterior, es decir dividiendo cada segmento en diez partes iguales. Pero también existe otra forma de hacerlo, y es agregando números a la derecha. Usemos este procedimiento para responder a la pregunta.

 

Tenemos los números 0.234 y 0.235, agregamos un cero a la derecha en ambos números: 0.2340 y 0.2350. De tal forma que encontramos 0.2341, 0.2342, 0.2343, 0.2344, 0.2345, 0.2346, 0.2347, 0.2348, y 0.2349. Listo, tenemos otros nueve números de los cuales elegir. Por ejemplo, 0.2345.

 

 

Con los decimales ya quedó muy claro, pero ¿cómo le hacemos con las fracciones si no tenemos a la mano el círculo que construimos? Por ejemplo, entre 3/6 y 5/6.

 

En este caso las fracciones tienen el mismo denominador, quiere decir que el entero está dividido en seis partes iguales, y entre 3 y 5 está el 4, así sabemos que entre 3/6 y 5/6 está la fracción 4/6.

 

Pero ¿Qué pasa cuando queremos encontrar un número entre 1/3 y 2/3?

 

Presta atención, en el segmento de recta del 0 al 1, colocaremos las fracciones correspondientes a los tercios. Así obtenemos 1/3, 2/3 y el entero. Ahora dividiremos el segmento de 1/3 a 2/3 a la mitad. ¿Observas algo peculiar?

 

 

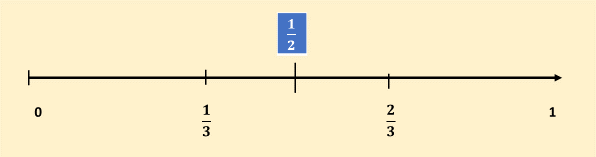
El número que buscamos es la mitad del entero, es decir, 1/2.

 

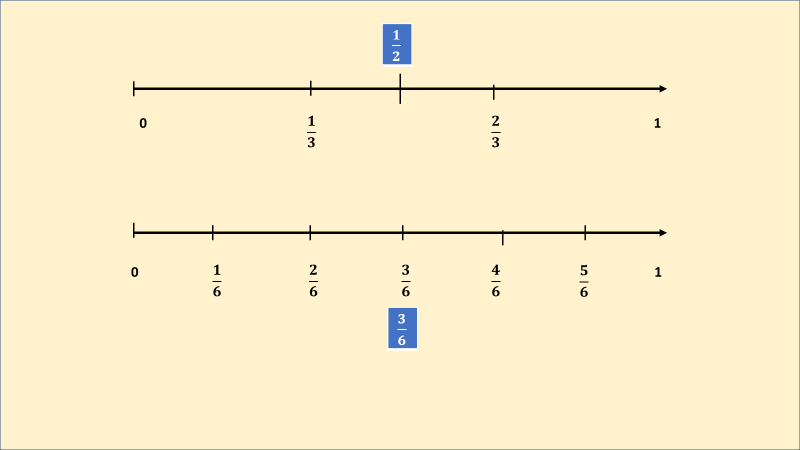
Comprobemos con una fracción equivalente a ½ = 3/6. Dividamos el segmento en seis partes iguales, así 1/6, 2/6, 3/6, 4/6, 5/6. De esta forma podemos comprobar que, efectivamente, ½ es la fracción que se encuentra exactamente a la mitad de 1/3 y 2/3.

 

 

Considera que también puedes trabajar la fracción con su expansión decimal, es decir, dividir el numerador entre el denominador y con ello tendrás un número decimal que representa a la fracción. Comprobemos, de esta manera, las respuestas de la actividad con el círculo.

 

Las fracciones 1/4 y 1/2 se encuentra la fracción 3/8. Dividamos las tres fracciones para comprobar si la respuesta es correcta.

 

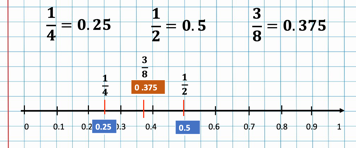
Para la fracción un cuarto, tenemos que uno entre cuatro es igual a 0.25, en el caso de un medio, uno entre dos es igual a 0.5 y para tres octavos, tres entre 8 es igual a 0.375.

Identificamos los números en la recta numérica y, efectivamente, entre los números 0.25 y 0.5 encontramos el 0.375, es decir, entre ¼ y ½ está la fracción 3/8.

 

 

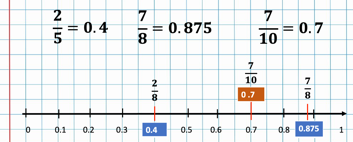
Perfecto, ahora entre las fracciones 2/5 y 7/8 estaba la fracción 7/10. Verifiquemos. Dividimos 2 entre 5, igual a 0.4, 7 entre 8 es igual a 0.875 y 7/10 es 0.7. Identificamos los números en la recta numérica, por lo tanto, comprobamos que la respuesta fue correcta, ya que entre 0.4 y 0.875 encontramos el 0.7. Entonces demostramos que entre 2/5 y 7/8 está la fracción 7/10.

 

 

En esta sesión revisaste varios conceptos: números naturales, números racionales, densidad de las fracciones y decimales, etcétera. Comparte tus reflexiones con tu maestra o maestro para recibir retroalimentación a distancia, cuando sea posible.

SEC1-CIE-15ENE

 

CIENCIAS  - SECUNDARIA 1

De los científicos para el mundo

(VIERNES 15 ENERO)

ACTIVIDAD:

Observa los siguientes objetos.

 

 

Observa con detenimiento y pon mucha atención, porque el reto de esta sesión será escribir en tu cuaderno qué tienen en común estos objetos con las aportaciones que se compartieron de cada uno de los científicos. Al final comenta tus conclusiones con su profesora o profesor de Biología.

RESUMEN:

Quizás alguna vez hayas visto o leído una revista de ciencia, ¿Sabías que los científicos pueden trabajar en cualquier área y son de todas las naciones del mundo?

 

Así es, incluso en esta tarea científica se puede encontrar personal de todas las profesiones: químicos, físicos, ingenieros, matemáticos, programadores de computadoras, bibliotecarios, entre otros.

 

Ahora, lee un breve artículo escrito por Martín Bonfil Olivera, un químico y divulgador científico mexicano, para que comprendas un poco más sobre lo que quiere decir la palabra ciencia. El artículo se titula:

 

“La ciencia básica es… ¡básica!

 

Cuando se habla de grandes empresas científicas como el Proyecto del Genoma Humano, que descifró la información genética completa de nuestra especie, o el Gran Colisionador de Hadrones, recientemente echado a andar para desentrañar varios de los misterios más profundos de la física, es común que surja una pregunta: ¿vale la pena? La preocupación es válida: los dos proyectos mencionados tuvieron, cada uno, un costo aproximado de 10,000 millones de dólares. ¿Se justifica gastar esa cantidad en la llamada “ciencia básica”, en vez de invertirla, digamos, en combatir el hambre o la pobreza? Pero la pregunta lleva ya, implícitamente, cierto prejuicio: que la ciencia básica “no sirve para nada”. Para nada más, claro, que para entender la naturaleza.

Después de leer, es importante que sepas que los grandes avances en ciencia y tecnología tienen su origen en las ideas de personas que tal vez comienzan su formación científica en las aulas o escuelas.

 

Aunque la gente vive aparentemente alejada de la ciencia, el conocimiento científico está presente en la vida de todas las personas y en tu formación básica puedes obtener recursos para comprender el mundo que te rodea y cómo funciona; y así tomar mejores decisiones individuales y colectivas. Desde evaluar los riesgos a la salud, hasta los peligros de la contaminación, la deforestación, las presas, la energía nuclear o la minería a cielo abierto. Lo notes o no, el conocimiento es necesario para tu bienestar.

 

Los científicos pueden aportar información, ideas y habilidades analíticas para enfrentar asuntos de interés público. A menudo, pueden ayudar al público y a sus representantes a comprender las causas probables de fenómenos, como desastres naturales.

 

En México, se cuenta con el servicio sismológico nacional que proporciona información necesaria para mejorar nuestra capacidad de evaluar y prevenir el riesgo sísmico y volcánico a nivel nacional. Este servicio está a cargo de un equipo de científicos especialistas en las ciencias de la Tierra, que se encargan de interpretar los datos sísmicos.

 

¿Te parece que la investigación que se genera en este campo de las ciencias, es de interés de la sociedad en general?

 

Así es, el trabajo de estos científicos tiene un impacto significativo en la vida y sobrevivencia ante un evento natural. Al vivir en una región del planeta con alta sismicidad, en este país se ha desarrollado una cultura de protección civil ante los desastres naturales. Por lo que, el trabajo de los científicos y las actitudes de responsabilidad han salvado cientos de vidas en México.

 

Pero, ¿dónde se encuentran los científicos?

 

Los científicos se encuentran trabajando en universidades, hospitales, negocios e industrias, gobierno, organizaciones de investigación independientes y asociaciones científicas. Sus actividades, se convierten en aportaciones que favorecen el avance en el conocimiento y aprovechamiento racional del ambiente y los recursos de los que se sirven las personas.

 

Debido a la naturaleza social de la ciencia, la difusión de la información científica es fundamental para su progreso.

 

Ahora bien, ¿cómo presentan los científicos sus descubrimientos y teorías?

 

Los científicos pueden presentar sus teorías y descubrimientos de diversas maneras, pueden ser ensayos de sus teorías que se leen en juntas o se publican en revistas científicas, lo que va permeando a todos los rincones de la sociedad a través de las escuelas, museos y diversos medios de comunicación. Bien, ya sabes dónde encontrar información científica, como se menciona, la ciencia se encuentra en todos lados.

 

Ahora conocerás aportaciones de algunos científicos, la lista es larga, pero por el tiempo sólo se hablará de algunos de ellos.

 

Dra. Julieta Fierro.

Se empezará con la Dra. Julieta Fierro, que es astrónoma, y que ha incursionado en labores de educación mediante la producción y realización de series televisivas para educación a distancia, dirigidas a la enseñanza media y básica.

 

La labor de esta científica es muy importante pues la divulgación, es el puente de comunicación entre los descubrimientos científicos y las actividades que se realizan en la vida cotidiana.

 

Dr. Mario Molina.

El siguiente es el Dr. Mario Molina. Quien investigó acerca de la contaminación atmosférica, y el efecto que tienen esos gases en el desgaste de la capa de ozono; incluso colaboró en algunos proyectos para enfrentar el problema de la degradación de la calidad del aire.

 

A partir del 2005 presidió un centro de investigación y promoción de políticas públicas que lleva su nombre, donde realizó estudios estratégicos sobre energía y medio ambiente. Las investigaciones del Dr. Molina permiten reconocer las actividades y productos que deterioran la capa de ozono, la cual protege de la radiación ultravioleta del Sol.

 

Dra. Edna Leticia González.

También está la Dra. Edna Leticia González. Cuya investigación se centra en mejorar el conocimiento de los anfibios nativos de México. Durante esta investigación se percató que la disminución de la población de anfibios era causada por la inserción del ser humano dentro de su hábitat, con actividades como la agricultura.

 

Muchos de los humanos consideran estos anfibios como plagas, sin embargo, estos organismos son depredadores de una gran cantidad de insectos, que atacan directamente a los cultivos o a los humanos.

 

Las aportaciones de la Dra. Edna González, contribuyen al conocimiento del funcionamiento de los ecosistemas y así tomar medidas para evitar el deterioro de los mismos.

 

Dr. José Sarukhán.

Otro científico es el Dr. José Sarukhán cuyo trabajo se ha enfocado en el estudio de los ciclos biogeoquímicos en selvas tropicales, los estudios sobre la biodiversidad en México y los problemas ambientales globales y de desarrollo sustentable.

 

Sus investigaciones han sido la base para cientos de estudios para comprender el flujo de materia en los ecosistemas y ha brindado información para reconocer cuáles son los materiales que se utilizan en casa y los residuos que terminan en los cuerpos de agua, alterando los ciclos biogeoquímicos, cuyas consecuencias ya se han estudiado.

 

Dra. María del Socorro Flores González.

Ahora se hablará de una importante aportación al terreno de las ciencias de la salud, la Dra. María del Socorro Flores González quien desarrolló un método para diagnosticar amibiasis invasiva, que permite detectar con mayor rapidez este padecimiento.

 

La amibiasis es una infección producida por un microorganismo que afecta el tracto intestinal y al hígado preferentemente. La transmisión de la enfermedad es por vía fecal-oral o bien de forma indirecta, mediante la ingesta de agua o de alimentos contaminados. Esto te puede llevar a la reflexión de que es mejor consumir alimentos preparados en casa.

 

Dr. Hugo Balleza Tapia.

Finalmente, se comenta sobre otro científico de esa misma área, el Dr. en Ciencias Hugo Balleza Tapia cuya investigación se centra en los mecanismos celulares y moleculares en la Enfermedad de Alzheimer.

 

Enfocándose en las condiciones patológicas que deterioran la salud humana, siendo un padecimiento característico de la edad adulta mayor y que se está convirtiendo en un problema de salud pública a nivel mundial dado el incremento de la población mayor a 65 años.

 

Recientemente el Dr. Balleza Tapia ha incursionado en el área de la ciencia aplicada enfocando su investigación en el desarrollo de terapias con anticuerpos contra enfermedades de alto impacto en la sociedad como el dolor crónico derivado de enfermedades como la diabetes. Y que importante es estar atentos en la prevención de los padecimientos que llegan con la edad. Aunque estos padecimientos tienen un componente genético, los hábitos alimenticios pueden hacer la diferencia.

 

Como has podido leer, hay muy buenas aportaciones de estos grandes científicos, sin duda alguna han beneficiado la vida cotidiana de todas las personas, desde el cuidado del entorno en el que viven hasta en su salud.

 

Sin embargo, durante estas investigaciones los científicos se enfrentan a diversas situaciones, no sólo tienen la labor de la investigación sino de que esa investigación o los resultados no dañen o perjudiquen la biodiversidad.

 

Si recuerdas al inicio del primer trimestre se abordó la importancia de la ética en la biodiversidad, e incluso en el “Abecedario Biológico” incluiste la palabra bioética, revísala, ya que es una palabra clave en el trabajo científico.

 

Pero, ¿qué tiene que ver la bioética con todo ese trabajo que hacen los científicos?

 

La respuesta es que, cuando se habla del avance en el ámbito científico, la sociedad la misma comunidad científica creen que pueden hacer investigaciones y experimentos de cualquier cosa y en ocasiones sin importar pueden provocar daños a la salud o al medio. Sin embargo, esto no es así, la ciencia tiene normas éticas y se basa en tres principios.

 

El primer principio es el de beneficencia, y se refiere a que todos los trabajos científicos deben estar direccionados a hacer el bien a la vida y la sociedad misma.

 

Es importante saberlo, ya que una de las polémicas que han existido es acerca de la modificación de organismos vivos a nivel molecular, con ayuda de la ingeniería genética.

 

En el área de la salud, este campo está enfocado en mejorar los tratamientos contra el cáncer, en la producción de hormonas, vacunas contra infecciones como hepatitis B, gripe, tuberculosis, e incluso el virus de inmunodeficiencia humana (VIH).

 

Hay una pregunta que surge mucho y es: ¿Se tiene derecho a manipular el patrimonio genético de las especies o sería mejor dejar que la naturaleza siga su curso?

 

Bien, con relación a esta pregunta, se encuentra el segundo principio referente a la autonomía, y el cual habla de la capacidad que tiene cada persona sobre tomar la responsabilidad de sus propias acciones.

 

Dentro de una investigación científica, este principio va ligado al consentimiento informado, concreto, y sobre todo voluntario de la persona que va a ser partícipe en esa investigación.

 

Los científicos dentro de su labor en este consentimiento, deberán explicar a detalle en qué consistirá la investigación, tomando en cuenta que se tienen que respetar las visiones y derechos de los seres humanos.

 

Por último, se tiene el tercer principio, la justicia requiere la distribución justa y equitativa de los beneficios y riesgos de la participación.

 

La justicia prohíbe la exposición de un grupo de personas a los riesgos de la investigación exclusivamente para el beneficio de otro grupo. Los representantes comunitarios tienen la responsabilidad de garantizar que la participación de la comunidad en un estudio de investigación esté justificada.

 

Como te darás cuenta toda investigación tiene bases y principios éticos, cuya única finalidad es el bien de la sociedad y de la biodiversidad.

 

Casi llegas al final, pero antes es importante que rescates la idea de que el trabajo científico no es ajeno a las necesidades de las personas, al contrario, se pueden encontrar evidencias de su labor en la forma en que te cuides y en los productos que consumes. Además, que el avance científico debe ir acompañado de un carácter de responsabilidad hacia toda la naturaleza, pues al ser parte de ella, nos te verás beneficiado o perjudicado.

 

Ha llegado el momento de agregar otra palabra a tu “Abecedario Biológico”. El concepto que se retoma es el de investigación, que es la base de todo descubrimiento científico. ¿Qué te parece?

 

Anótalo y busca su definición, puedes comenzar por revisar tu libro de texto.

 

Has terminado la sesión.