ESPAÑOL - SECUNDARIA 1
Causa-efecto en los cuentos
(JUE 03 DICIEMBRE)
ACTIVIDAD:
Como reto final, se propone organizar los hechos de tu cuento: establece cuáles acontecimientos desencadenarán otras situaciones, así como sus consecuencias.
Recuerda hacer uso de los nexos de causa que repasaste en esta sesión.
RESUMEN:
¿Alguna vez has escuchado o leído historias en donde los hechos no guardan relación entre sí?
Por ejemplo:
“Toda la semana fui al gimnasio y al box, porque me gusta ir a la escuela y me gusta comer con mis amigos. Me levanté por la mañana y todo parecía normal, hasta que llegué a casa; me dolía mucho el estómago y sólo me dormí y me puse pomada para que no me doliera”.
¿Qué rara manera de contar, no crees?, ¿qué tiene que ver lo de comer con sus amigos con el box?
Como te diste cuenta, en el ejemplo anterior no se especifica o es confuso establecer qué ocurrió primero y qué después o por qué sucedió. Sin embargo, es claro que la causa es el exceso de ejercicio y la consecuencia el dolor de estómago. Incluso hay hechos que no se relacionan con el relato porque no es clara la relación que existe entre que, al protagonista, le guste ir a la escuela y a comer con sus amigos; y el hecho de que por ir al box le dolió el estómago.
Las relaciones de causa y efecto son recursos discursivos que ayudan a ser claros al momento de escribir un cuento o cualquier tipo de texto narrativo.
Las relaciones causales pueden seguir una trama lineal de la historia, esto es: comenzar por el inicio de los acontecimientos, seguido del desarrollo de la historia o situación de la cual se está hablando o comunicando; posteriormente, ubicar un espacio donde se genere un conflicto o suspenso en los lectores u oyentes, para terminar con un desenlace donde se conoce lo que ocurrió al final.
Aunque no siempre puede hacerse de esta manera, pues existen otras formas de contar una historia; sin embargo, deben ser claras las relaciones de causa-efecto para que el texto presente coherencia y cohesión, es decir, que sea entendible.
¿Cómo reestructurarías el fragmento del cuento anterior?
Revisa la siguiente propuesta.
“Toda la semana he ido al gimnasio y al box porque me gusta hacer ejercicio. Hoy, cuando llegué a casa, me dolía mucho el estómago; yo creo que fue porque hice ejercicio de más. Me tomé una pastilla y me acosté para dormir un rato”.
Así queda mejor la propuesta de redacción, porque no hay elementos que te distraigan, y queda muy claro que se está narrando una acción y su consecuencia.
Ahora se realizará una remembranza de la estructura textual de los cuentos, sólo para analizar la forma en que se irán escribiendo los acontecimientos. Eso sí, recuerda que existen otras formas de narrar los hechos, pero en este momento se abordará la estructura clásica de los cuentos, que se le conoce como trama lineal.
Estructura de los cuentos
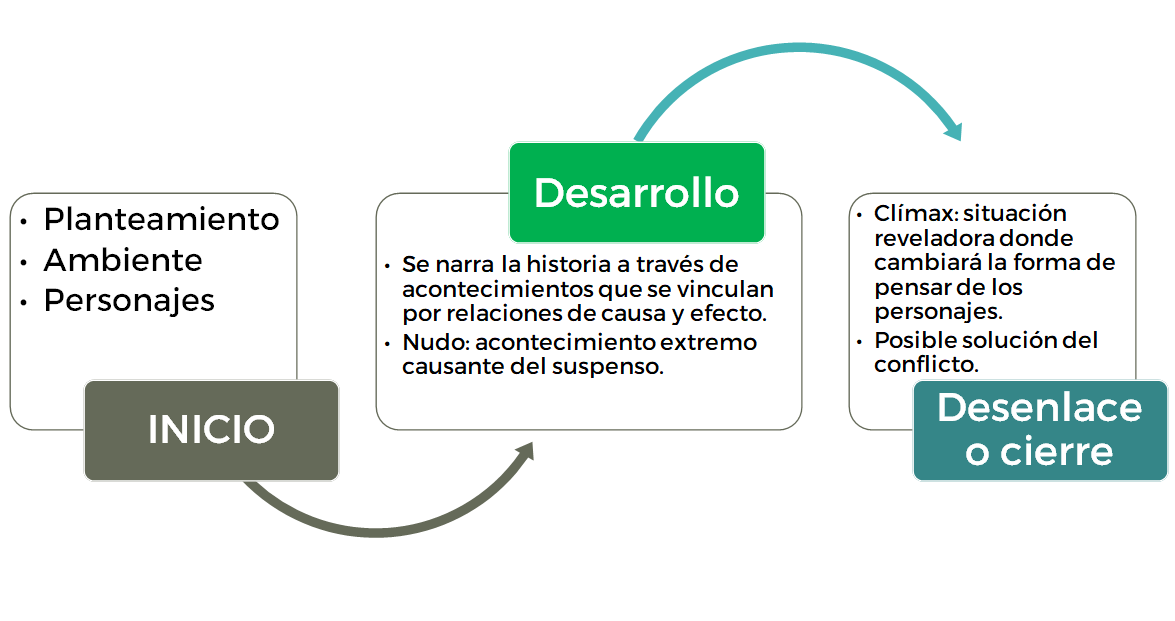
En el inicio se plantea el ambiente que es el lugar donde ocurrirán los acontecimientos, en éste se mencionan además los personajes que participarán en ella y se planea la situación inicial que desencadenará la historia.
En seguida se continúa con el desarrollo que da lugar a los hechos narrativos mediante relaciones de causa y efecto.
En este apartado se suelen narrar los sucesos de manera cronológica.
Bajo esta estructura de trama lineal se sugiere que el texto comience por un inicio, un desarrollo, y un desenlace. Sin embargo, es importante mencionar que existen varios tipos de trama, como: la circular o en espiral, las cuales pueden iniciar contando el final, o que terminen con un final abierto.
El nudo: acontecimiento extremo causante del suspenso.
El clímax: situación reveladora donde cambiará la forma de pensar de los personajes.
Por último, el desenlace da cierre al cuento y aquí es donde se va a resolver o no el conflicto.
Ya que hiciste un repaso por la estructura tradicional de los cuentos, es momento de revisar cómo se construye la trama. Los acontecimientos en un cuento se construyen como si fueran piezas de un rompecabezas: un acontecimiento se relaciona con otros para armar una historia. Es decir, cada acontecimiento impacta a otro y genera relaciones de causa y efecto entre ellos.
Por ejemplo, en el cuento que leíste al inicio de la sesión se menciona que el protagonista hizo ejercicio de más en un gimnasio (ese es un acontecimiento), y como consecuencia le dolió el estómago (ese es el efecto que causó). Mencionar que le gusta ir a la escuela y comer con sus amigos no se relaciona, pues no tiene ningún efecto en la historia.
Las relaciones de causa y efecto en un texto narrativo permiten a los lectores encontrarle sentido a la historia, es decir, son las pautas para continuar escribiendo hechos o acontecimientos que guardan relación entre sí y dan cuerpo al cuento.
Para ejemplificar de una mejor manera los efectos causales en un cuento, Ahora leerás un fragmento del cuento de terror: “El almohadón de plumas” del escritor Horacio Quiroga. Conforme avances en la lectura, se irán señalando las relaciones de causa y consecuencia entre los acontecimientos.
La historia dice así:
“Su luna de miel fue un largo escalofrío. Rubia, angelical y tímida, el carácter duro de su marido heló sus soñadas niñerías de novia. Lo quería mucho, sin embargo, a veces con un ligero estremecimiento cuando volviendo de noche juntos por la calle, echaba una furtiva mirada a la alta estatura de Jordán, mudo desde hacía una hora. La casa en que vivían influía un poco en sus estremecimientos. La blancura del patio silencioso —frisos, columnas y estatuas de mármol— producía una otoñal impresión de palacio encantado. Dentro, el brillo glacial del estuco, sin el más leve rasguño en las altas paredes, afirmaba aquella sensación de desapacible frío”.
¿Qué te pareció el principio?
Al leerlo tal vez sientas que esto no va a acabar bien. Ya verás qué es lo que pasa.
Lo que acabas de leer es el inicio del cuento que te presenta la situación inicial: una muchacha acaba de casarse con un hombre de carácter duro, y el aspecto de la casa donde viven, le provoca una sensación de malestar; de preocupación.
Ahora, continua con la lectura.
“No es raro que adelgazara. Tuvo un ligero ataque de influenza que se arrastró insidiosamente días y días; Alicia no se reponía nunca”.
Hasta aquí otra pauta.
Como leíste se enfermó Alicia. ya conociste el primer acontecimiento de la historia, ¿qué consecuencias consideras que esto tendrá?
¡Descúbrelo!
“Fue ese el último día que Alicia estuvo levantada. Al día siguiente amaneció desvanecida. El médico de Jordán la examinó con suma atención, ordenándole calma y descanso absoluto”.
Al analizar esta parte de la historia, la primera consecuencia fue que Alicia no mejoró, sino que empeoró. Otra consecuencia fue que el médico le recomendó descanso absoluto. suponer que entonces la muchacha no se levantaba de su cama. ¿Qué consecuencia consideras que esto desencadenó?
Bien. ¡Continua con la lectura!
“Al otro día Alicia seguía peor. Hubo consulta. Constatándose una anemia de marcha agudísima, completamente inexplicable. Alicia no tuvo más desmayos, pero se iba visiblemente a la muerte. Todo el día el dormitorio estaba con las luces prendidas y en pleno silencio. Pasábanse horas sin oír el menor ruido. Alicia dormitaba. Jordán vivía casi en la sala, también con toda la luz encendida”.
Haz otra pausa en la lectura.
Analizando esta otra parte de la historia, puedes ver que la consecuencia de la enfermedad agravada de Alicia fue que toda la casa adquirió una atmósfera de quietud total; incluso su esposo, Jordán, contribuía a esta atmósfera. Es decir, se van poniendo peor y peor las cosas.
Como observas los elementos causales y de consecuencia del cuento a lo largo del desarrollo, abren paso al nudo, donde tiene lugar el suspenso o terror, en el caso de los textos que pertenecen a estos géneros.
Si quieres saber en qué termina, y cuál es la suerte de Alicia, continua con la lectura de este cuento, que se encuentra fácilmente en bibliotecas físicas o en bibliotecas digitales. Recuerda, el título de este libro es: “El almohadón de plumas”, de Horacio Quiroga.
Volviendo al tema. La construcción de la trama de una narración requiere, además de elegir el orden en que son contados los acontecimientos, seleccionar los que se presentan en el texto. Esto significa que la creación de una trama exige una labor de selección y combinación.
Al plantear una trama, el autor se pregunta: ¿qué sucesos que yo sé, formarán parte de la historia que contaré y cuáles no? (por ejemplo, contaré que Alicia enfermó de anemia que después resultó ser un caso grave de influenza, pero no diré la verdadera causa porque esto abrirá paso al nudo del cuento y creará suspenso en la historia).
También se pregunta: ¿en qué orden pondré aquello que contaré? (por ejemplo: comenzar por describir la enfermedad de Alicia, seguir con los síntomas que presentaba y que asociaban los médicos y culminar cuando el médico determina su muerte y todos saben al fin la verdad).
Respondiendo preguntas como las anteriores, se realiza la selección y combinación de acontecimientos que forman parte de una trama narrativa.
Observa el siguiente video para reforzar la explicación.
- “Causas y consecuencias en el cuento”.
https://www.youtube.com/watch?v=9i5YemwfAU8&t=10s
Como viste, el cuento es un relato breve que narra sucesos o acciones en los que se involucra a los personajes en un tiempo y lugar determinado. Está formado por tres momentos: una situación inicial, la aparición de un problema que tiene que resolverse y el final o la solución del conflicto.
Toda narración tiene una trama, es decir, el orden en que se cuentan los acontecimientos, que no necesariamente es el orden cronológico en el que sucedieron. Es decir, que el autor puede elegir contar su cuento en el orden que quiera.
Revisa un ejemplo de lo descrito anteriormente en el siguiente microcuento.
Señor juez, le repito que, si llego a saber qué pasaba gente justo por ahí, no hubiera tirado la casa por la ventana.
Como viste es muy curioso este cuento, dice muy poquitas cosas, pero con lo que dice, ya puedes imaginarte todo lo que pasó.
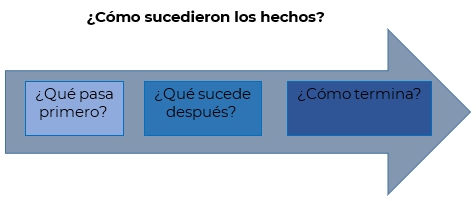
Así son los microcuentos o microrelatos. Ahora se analizará todo lo que se contó y en qué orden va cronológicamente.
¿Qué pasó primero?
La persona que está ante el juez echó, en sentido literal, “la casa por la ventana”.
¿Qué pasó después?
Gente que pasaba por ahí fue, con toda seguridad, aplastada por la casa.
¿Qué pasó al final?
La persona que echó la casa por la ventana fue llevada ante el juez, puede deducirse que antes de ello la aprehendió la policía.
¿En qué orden contaron los hechos en el cuento?, ¿por dónde empezaron?
Los hechos se contaron en este orden: empezando por el final (la presentación ante el juez) y continuando por el inicio y el desarrollo (había gente que pasaba, pero no fue vista por la persona que “echó la casa por la ventana”, así que ocurrió un accidente.
Como has visto, existen distintas opciones para contar una historia, como éstas:
- Iniciar contando el desarrollo de los acontecimientos y poco a poco ir develando cómo inició todo para concluir con el final.
- Iniciar con el final de los acontecimientos y luego contar cómo comenzó la historia para terminar con el desarrollo de los sucesos.
- También se puede contar la historia tal y como sucedieron los hechos, es decir, en orden cronológico.
La trama y las relaciones de causa-efecto del cuento generan un efecto distinto en la forma como se cuenta la historia, y, por tanto, en el lector. Basta con tener una idea general del conflicto en el cuento que se escribe. No importa si por ahora no está claro cómo serán los personajes, los espacios ni los ambientes.
Para que te vayas familiarizando, realiza la siguiente actividad:
Aventúrate a escribir un cuento breve. Para ello, primero ordena cronológicamente los hechos que quieres narrar. Después decide cómo narrar la historia, es decir, en qué orden la contarás. Recuerda que también es válido hacerlo en orden cronológico.
Guíate con los siguientes elementos.
Primero, elabora en tu cuaderno los dos esquemas siguientes y complétalos.
En el Esquema 1 se consideran los elementos de la historia de manera cronológica.
En el Esquema 2 se decide como contar la historia y los hechos de la misma.
¿Cómo contarán la historia? ¿En qué orden presentarán los hechos?

Una vez que identificaste los hechos que conformarán la trama, analiza los recursos del lenguaje que sirven para establecer las relaciones entre los sucesos.
Al narrar lo que sucede en un cuento, es necesario expresar las causas que los provocan.
Analiza el siguiente ejemplo:
Eché una ligera ojeada sin acercarme demasiado porque no me gusta contemplar cadáveres…
El nexo “porque” explica la causa por la cual no se acercó mucho.
Para reforzar lo aprendido revisa algunos recursos para expresar causalidad en los cuentos:

Esos nexos ayudan a expresar consecuencia.
Ahora, se sugiere hacer una lista en tu cuaderno incluyendo otros ejemplos.
Para comprender mejor el tema, apóyate en tu libro de texto de Lengua Materna, ubica el aprendizaje esperado: Escribe cuentos de un subgénero de su preferencia, y realiza las actividades relacionadas con cómo vincular acontecimientos de forma causal.
Pide a un familiar o amigo que lea tus cuentos para que observen si lo has hecho de manera secuencial, con coherencia y cohesión. También puedes consultar páginas de internet de fuentes confiables que refuercen este contenido.
Finalmente, se recomienda leer cuentos. Puedes comenzar con “El almohadón de plumas”, de Horacio Quiroga, y después aventurarte a explorar títulos y autores diversos hasta que encuentres aquellos que son de tu completo agrado. Descubrirás en la lectura un mundo maravilloso. Has concluido el tema de hoy.
Como reto final, se propone organizar los hechos de tu cuento: establece cuáles acontecimientos desencadenarán otras situaciones, así como sus consecuencias.
Recuerda hacer uso de los nexos de causa que repasaste en esta sesión.
¿Alguna vez has escuchado o leído historias en donde los hechos no guardan relación entre sí?
Por ejemplo:
“Toda la semana fui al gimnasio y al box, porque me gusta ir a la escuela y me gusta comer con mis amigos. Me levanté por la mañana y todo parecía normal, hasta que llegué a casa; me dolía mucho el estómago y sólo me dormí y me puse pomada para que no me doliera”.
¿Qué rara manera de contar, no crees?, ¿qué tiene que ver lo de comer con sus amigos con el box?
Como te diste cuenta, en el ejemplo anterior no se especifica o es confuso establecer qué ocurrió primero y qué después o por qué sucedió. Sin embargo, es claro que la causa es el exceso de ejercicio y la consecuencia el dolor de estómago. Incluso hay hechos que no se relacionan con el relato porque no es clara la relación que existe entre que, al protagonista, le guste ir a la escuela y a comer con sus amigos; y el hecho de que por ir al box le dolió el estómago.
Las relaciones de causa y efecto son recursos discursivos que ayudan a ser claros al momento de escribir un cuento o cualquier tipo de texto narrativo.
Las relaciones causales pueden seguir una trama lineal de la historia, esto es: comenzar por el inicio de los acontecimientos, seguido del desarrollo de la historia o situación de la cual se está hablando o comunicando; posteriormente, ubicar un espacio donde se genere un conflicto o suspenso en los lectores u oyentes, para terminar con un desenlace donde se conoce lo que ocurrió al final.
Aunque no siempre puede hacerse de esta manera, pues existen otras formas de contar una historia; sin embargo, deben ser claras las relaciones de causa-efecto para que el texto presente coherencia y cohesión, es decir, que sea entendible.
¿Cómo reestructurarías el fragmento del cuento anterior?
Revisa la siguiente propuesta.
“Toda la semana he ido al gimnasio y al box porque me gusta hacer ejercicio. Hoy, cuando llegué a casa, me dolía mucho el estómago; yo creo que fue porque hice ejercicio de más. Me tomé una pastilla y me acosté para dormir un rato”.
Así queda mejor la propuesta de redacción, porque no hay elementos que te distraigan, y queda muy claro que se está narrando una acción y su consecuencia.
Ahora se realizará una remembranza de la estructura textual de los cuentos, sólo para analizar la forma en que se irán escribiendo los acontecimientos. Eso sí, recuerda que existen otras formas de narrar los hechos, pero en este momento se abordará la estructura clásica de los cuentos, que se le conoce como trama lineal.
Estructura de los cuentos

En el inicio se plantea el ambiente que es el lugar donde ocurrirán los acontecimientos, en éste se mencionan además los personajes que participarán en ella y se planea la situación inicial que desencadenará la historia.
En seguida se continúa con el desarrollo que da lugar a los hechos narrativos mediante relaciones de causa y efecto.
En este apartado se suelen narrar los sucesos de manera cronológica.
Bajo esta estructura de trama lineal se sugiere que el texto comience por un inicio, un desarrollo, y un desenlace. Sin embargo, es importante mencionar que existen varios tipos de trama, como: la circular o en espiral, las cuales pueden iniciar contando el final, o que terminen con un final abierto.
El nudo: acontecimiento extremo causante del suspenso.
El clímax: situación reveladora donde cambiará la forma de pensar de los personajes.
Por último, el desenlace da cierre al cuento y aquí es donde se va a resolver o no el conflicto.
Ya que hiciste un repaso por la estructura tradicional de los cuentos, es momento de revisar cómo se construye la trama. Los acontecimientos en un cuento se construyen como si fueran piezas de un rompecabezas: un acontecimiento se relaciona con otros para armar una historia. Es decir, cada acontecimiento impacta a otro y genera relaciones de causa y efecto entre ellos.
Por ejemplo, en el cuento que leíste al inicio de la sesión se menciona que el protagonista hizo ejercicio de más en un gimnasio (ese es un acontecimiento), y como consecuencia le dolió el estómago (ese es el efecto que causó). Mencionar que le gusta ir a la escuela y comer con sus amigos no se relaciona, pues no tiene ningún efecto en la historia.
Las relaciones de causa y efecto en un texto narrativo permiten a los lectores encontrarle sentido a la historia, es decir, son las pautas para continuar escribiendo hechos o acontecimientos que guardan relación entre sí y dan cuerpo al cuento.
Para ejemplificar de una mejor manera los efectos causales en un cuento, Ahora leerás un fragmento del cuento de terror: “El almohadón de plumas” del escritor Horacio Quiroga. Conforme avances en la lectura, se irán señalando las relaciones de causa y consecuencia entre los acontecimientos.
La historia dice así:
“Su luna de miel fue un largo escalofrío. Rubia, angelical y tímida, el carácter duro de su marido heló sus soñadas niñerías de novia. Lo quería mucho, sin embargo, a veces con un ligero estremecimiento cuando volviendo de noche juntos por la calle, echaba una furtiva mirada a la alta estatura de Jordán, mudo desde hacía una hora. La casa en que vivían influía un poco en sus estremecimientos. La blancura del patio silencioso —frisos, columnas y estatuas de mármol— producía una otoñal impresión de palacio encantado. Dentro, el brillo glacial del estuco, sin el más leve rasguño en las altas paredes, afirmaba aquella sensación de desapacible frío”.
¿Qué te pareció el principio?
Al leerlo tal vez sientas que esto no va a acabar bien. Ya verás qué es lo que pasa.
Lo que acabas de leer es el inicio del cuento que te presenta la situación inicial: una muchacha acaba de casarse con un hombre de carácter duro, y el aspecto de la casa donde viven, le provoca una sensación de malestar; de preocupación.
Ahora, continua con la lectura.
“No es raro que adelgazara. Tuvo un ligero ataque de influenza que se arrastró insidiosamente días y días; Alicia no se reponía nunca”.
Hasta aquí otra pauta.
Como leíste se enfermó Alicia. ya conociste el primer acontecimiento de la historia, ¿qué consecuencias consideras que esto tendrá?
¡Descúbrelo!
“Fue ese el último día que Alicia estuvo levantada. Al día siguiente amaneció desvanecida. El médico de Jordán la examinó con suma atención, ordenándole calma y descanso absoluto”.
Al analizar esta parte de la historia, la primera consecuencia fue que Alicia no mejoró, sino que empeoró. Otra consecuencia fue que el médico le recomendó descanso absoluto. suponer que entonces la muchacha no se levantaba de su cama. ¿Qué consecuencia consideras que esto desencadenó?
Bien. ¡Continua con la lectura!
“Al otro día Alicia seguía peor. Hubo consulta. Constatándose una anemia de marcha agudísima, completamente inexplicable. Alicia no tuvo más desmayos, pero se iba visiblemente a la muerte. Todo el día el dormitorio estaba con las luces prendidas y en pleno silencio. Pasábanse horas sin oír el menor ruido. Alicia dormitaba. Jordán vivía casi en la sala, también con toda la luz encendida”.
Haz otra pausa en la lectura.
Analizando esta otra parte de la historia, puedes ver que la consecuencia de la enfermedad agravada de Alicia fue que toda la casa adquirió una atmósfera de quietud total; incluso su esposo, Jordán, contribuía a esta atmósfera. Es decir, se van poniendo peor y peor las cosas.
Como observas los elementos causales y de consecuencia del cuento a lo largo del desarrollo, abren paso al nudo, donde tiene lugar el suspenso o terror, en el caso de los textos que pertenecen a estos géneros.
Si quieres saber en qué termina, y cuál es la suerte de Alicia, continua con la lectura de este cuento, que se encuentra fácilmente en bibliotecas físicas o en bibliotecas digitales. Recuerda, el título de este libro es: “El almohadón de plumas”, de Horacio Quiroga.
Volviendo al tema. La construcción de la trama de una narración requiere, además de elegir el orden en que son contados los acontecimientos, seleccionar los que se presentan en el texto. Esto significa que la creación de una trama exige una labor de selección y combinación.
Al plantear una trama, el autor se pregunta: ¿qué sucesos que yo sé, formarán parte de la historia que contaré y cuáles no? (por ejemplo, contaré que Alicia enfermó de anemia que después resultó ser un caso grave de influenza, pero no diré la verdadera causa porque esto abrirá paso al nudo del cuento y creará suspenso en la historia).
También se pregunta: ¿en qué orden pondré aquello que contaré? (por ejemplo: comenzar por describir la enfermedad de Alicia, seguir con los síntomas que presentaba y que asociaban los médicos y culminar cuando el médico determina su muerte y todos saben al fin la verdad).
Respondiendo preguntas como las anteriores, se realiza la selección y combinación de acontecimientos que forman parte de una trama narrativa.
Observa el siguiente video para reforzar la explicación.
- “Causas y consecuencias en el cuento”.
https://www.youtube.com/watch?v=9i5YemwfAU8&t=10s
Como viste, el cuento es un relato breve que narra sucesos o acciones en los que se involucra a los personajes en un tiempo y lugar determinado. Está formado por tres momentos: una situación inicial, la aparición de un problema que tiene que resolverse y el final o la solución del conflicto.
Toda narración tiene una trama, es decir, el orden en que se cuentan los acontecimientos, que no necesariamente es el orden cronológico en el que sucedieron. Es decir, que el autor puede elegir contar su cuento en el orden que quiera.
Revisa un ejemplo de lo descrito anteriormente en el siguiente microcuento.
Señor juez, le repito que, si llego a saber qué pasaba gente justo por ahí, no hubiera tirado la casa por la ventana.
Como viste es muy curioso este cuento, dice muy poquitas cosas, pero con lo que dice, ya puedes imaginarte todo lo que pasó.
Así son los microcuentos o microrelatos. Ahora se analizará todo lo que se contó y en qué orden va cronológicamente.
¿Qué pasó primero?
La persona que está ante el juez echó, en sentido literal, “la casa por la ventana”.
¿Qué pasó después?
Gente que pasaba por ahí fue, con toda seguridad, aplastada por la casa.
¿Qué pasó al final?
La persona que echó la casa por la ventana fue llevada ante el juez, puede deducirse que antes de ello la aprehendió la policía.
¿En qué orden contaron los hechos en el cuento?, ¿por dónde empezaron?
Los hechos se contaron en este orden: empezando por el final (la presentación ante el juez) y continuando por el inicio y el desarrollo (había gente que pasaba, pero no fue vista por la persona que “echó la casa por la ventana”, así que ocurrió un accidente.
Como has visto, existen distintas opciones para contar una historia, como éstas:
- Iniciar contando el desarrollo de los acontecimientos y poco a poco ir develando cómo inició todo para concluir con el final.
- Iniciar con el final de los acontecimientos y luego contar cómo comenzó la historia para terminar con el desarrollo de los sucesos.
- También se puede contar la historia tal y como sucedieron los hechos, es decir, en orden cronológico.
La trama y las relaciones de causa-efecto del cuento generan un efecto distinto en la forma como se cuenta la historia, y, por tanto, en el lector. Basta con tener una idea general del conflicto en el cuento que se escribe. No importa si por ahora no está claro cómo serán los personajes, los espacios ni los ambientes.
Para que te vayas familiarizando, realiza la siguiente actividad:
Aventúrate a escribir un cuento breve. Para ello, primero ordena cronológicamente los hechos que quieres narrar. Después decide cómo narrar la historia, es decir, en qué orden la contarás. Recuerda que también es válido hacerlo en orden cronológico.
Guíate con los siguientes elementos.
Primero, elabora en tu cuaderno los dos esquemas siguientes y complétalos.
En el Esquema 1 se consideran los elementos de la historia de manera cronológica.

En el Esquema 2 se decide como contar la historia y los hechos de la misma.
¿Cómo contarán la historia? ¿En qué orden presentarán los hechos?

Una vez que identificaste los hechos que conformarán la trama, analiza los recursos del lenguaje que sirven para establecer las relaciones entre los sucesos.
Al narrar lo que sucede en un cuento, es necesario expresar las causas que los provocan.
Analiza el siguiente ejemplo:
Eché una ligera ojeada sin acercarme demasiado porque no me gusta contemplar cadáveres…
El nexo “porque” explica la causa por la cual no se acercó mucho.
Para reforzar lo aprendido revisa algunos recursos para expresar causalidad en los cuentos:

Esos nexos ayudan a expresar consecuencia.
Ahora, se sugiere hacer una lista en tu cuaderno incluyendo otros ejemplos.
Para comprender mejor el tema, apóyate en tu libro de texto de Lengua Materna, ubica el aprendizaje esperado: Escribe cuentos de un subgénero de su preferencia, y realiza las actividades relacionadas con cómo vincular acontecimientos de forma causal.
Pide a un familiar o amigo que lea tus cuentos para que observen si lo has hecho de manera secuencial, con coherencia y cohesión. También puedes consultar páginas de internet de fuentes confiables que refuercen este contenido.
Finalmente, se recomienda leer cuentos. Puedes comenzar con “El almohadón de plumas”, de Horacio Quiroga, y después aventurarte a explorar títulos y autores diversos hasta que encuentres aquellos que son de tu completo agrado. Descubrirás en la lectura un mundo maravilloso. Has concluido el tema de hoy.




