ESPAÑOL - SECUNDARIA 1
Pongamos en orden las ideas
(LUNES 25 ENERO)
ACTIVIDAD:
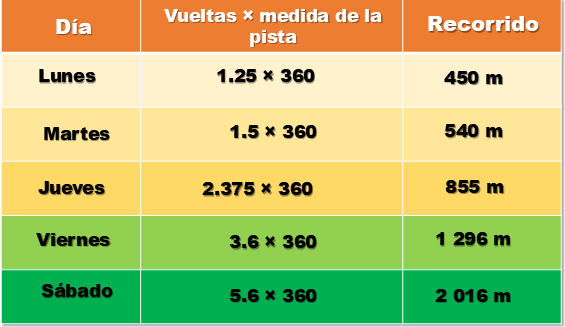
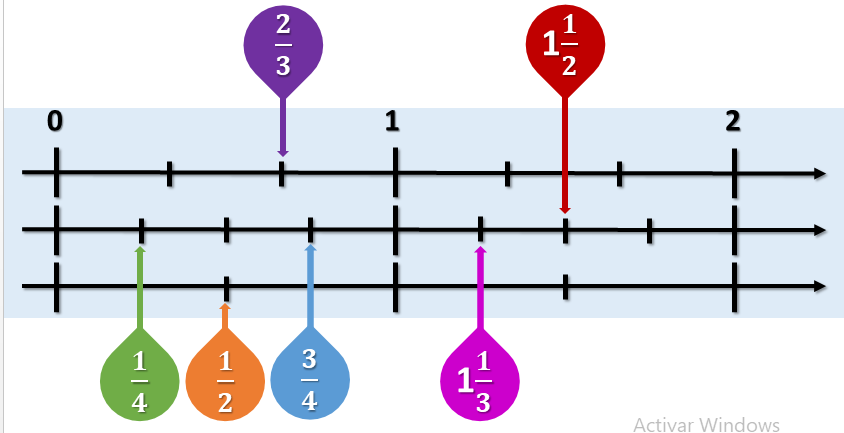
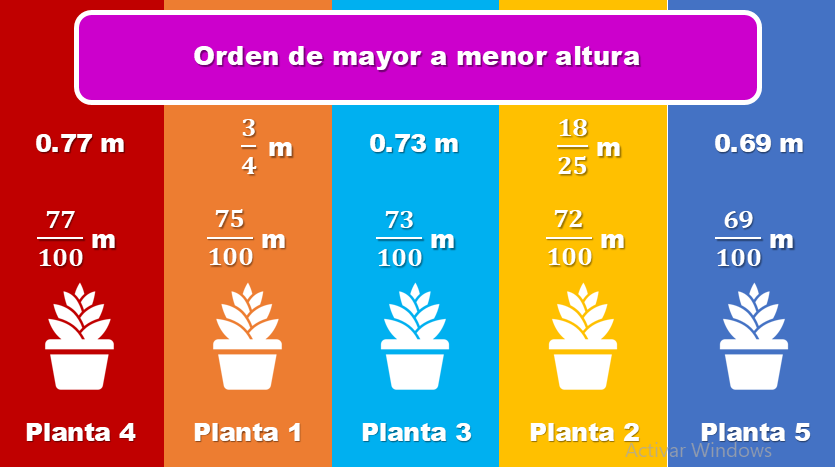
Observa la siguiente ficha de trabajo realizada por un compañero de secundaria y posteriormente analizarás qué tipo de información presenta y qué organizador gráfico podrías usar.

RESUMEN:
Comienza con la siguiente pregunta:
¿De qué manera podrías contar brevemente tu historia de vida, colocando las fechas y acontecimientos más importantes de forma cronológica?
Si recuerdas las lecturas de Historia, seguramente habrás podido observar que con frecuencia los sucesos más relevantes ocurridos durante un cierto periodo se presentan de manera concreta y secuencial en una línea de tiempo. Este ejemplo, la línea de tiempo, es un ejemplo de apoyo gráfico.
Un apoyo gráfico es una herramienta que se utiliza para mostrar datos de manera abreviada, con una interpretación fácil, que permite comparar información, ordenar en categorías, representar datos numéricos o lugares específicos en un espacio geográfico y señalar las partes de un objeto o las fases de un proceso. Los cuadros sinópticos, mapas mentales, conceptuales, tablas, gráficas, diagramas o líneas del tiempo forman parte de algunos ejemplos que conforman los diversos apoyos gráficos que existen.
Para conocer más sobre el tema y saber qué son los apoyos gráficos, qué tipos de organizadores existen y para qué se utilizan, observa la siguiente cápsula del minuto 1:22 al 4:41 .
- ¿Cómo leer y construir apoyos gráficos?
https://www.youtube.com/watch?v=GCsX8h-dfpg
Como pudiste observar, las fichas de trabajo son un recurso que permite registrar la información más importante de un tema de forma ordenada. En ocasiones, la información y datos recopilados se pueden presentar mediante una imagen o esquema, con palabras clave que permiten estructurar y sintetizar la información de manera visual, facilitando la comprensión, el análisis y la memoria del texto, al tiempo que se brinda una idea clara del contenido. A estas imágenes y esquemas se les conoce genéricamente como apoyos gráficos.
Sin duda, existe una amplia variedad de apoyos gráficos, compuestos por ideas o conceptos claves e imágenes o dibujos que explican el contenido, resumen la información y facilitan la comprensión del texto.
Para poder elaborar y utilizar los diferentes apoyos gráficos que existen, es necesario conocer los elementos y características que conforman cada uno. Así que a continuación revisarás los 5 organizadores gráficos más comunes.
En tu cuaderno elabora un cuadro comparativo como el que se presenta en la siguiente imagen:

En la primera columna enlista el nombre de los gráficos que se mencionen durante la sesión, seguido de cinco características específicas para cada recurso y finalmente, en la tercera sección, ejemplifica el diagrama con una imagen o dibujo.
Aprenderás sobre los cinco organizadores gráficos más frecuentes.
Número 5: Gráfica de barras
Un diagrama de barras, también conocido como gráfico de barras o columnas, es un elemento que sirve para representar y comparar con un solo golpe de vista un conjunto de datos o valores por categorías mediante recursos visuales. Las barras pueden orientarse horizontal y verticalmente, sin embargo, la altura de cada una será proporcional al número de datos o valores que represente.
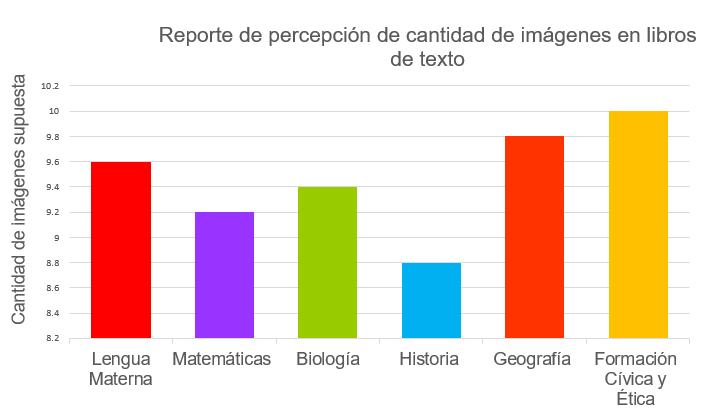
Por ejemplo: en esta gráfica se consideran los datos sobre la percepción de la cantidad de imágenes en los libros de texto. Si graficas la percepción sobre la cantidad de imágenes por página, podrás colocar los números obtenidos de forma vertical y las asignaturas de forma horizontal; diferenciándolas por colores, tal como se muestra en el ejemplo. El tamaño de las barras dependerá de los datos, en este caso, de la cantidad de imágenes percibida en los materiales de cada asignatura.
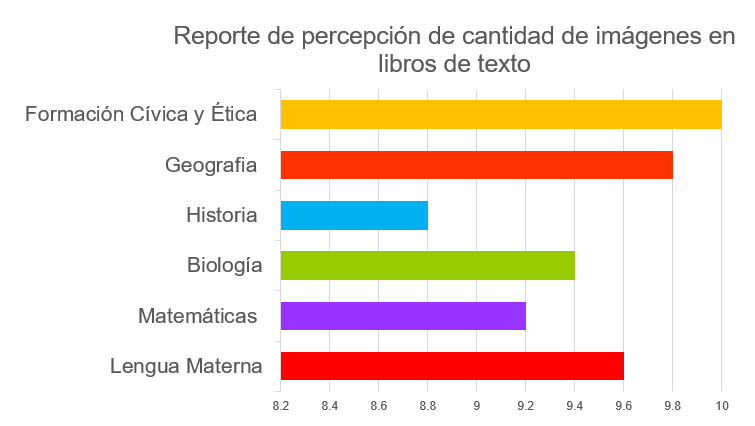
Otra forma de ordenar los datos es orientar las barras de manera vertical. En este ejemplo, los elementos aparecen de forma inversa, es decir, de manera vertical se enlistan todas las asignaturas mientras que de manera horizontal se coloca la cantidad de imágenes percibidas.
En ambos casos puedes agregar leyendas, componentes usados para identificar con mayor claridad los distintos elementos que conforman un gráfico, tales como colores o formas. Para este ejemplo se utilizan colores diferentes para representar cada asignatura.
Numero 4: Cuadro Sinóptico
El cuadro sinóptico es una estrategia que permite organizar y clasificar el contenido de un texto de manera sencilla para expresar visualmente las ideas principales de una temática y sus múltiples relaciones, partiendo del concepto general y dirigiéndolo hacia datos particulares, utilizando llaves para conectar la secuencia de la información, a través de una estructura lógica.
Sirve para contrastar los contenidos, anotando las semejanzas y diferencias, entre una o varias variables de un mismo tema. Pueden utilizarse como estrategias de enseñanza para organizar las ideas que aprendas durante tus clases.
Para elaborar un cuadro sinóptico de manera fácil, puedes dividir el contenido en subtemas y describir estos dentro de subdivisiones o llaves; así los conceptos o palabras claves que utilices estarán clasificados y descritos brevemente, facilitando la comprensión y memorización del tema.
Por ejemplo: si elaboras un cuadro sinóptico de los diferentes deportes que existen, primero puedes colocar el tema central, “deportes”, después puedes agregar dos categorías: los deportes individuales y los deportes que se practican en equipo; posteriormente, en esas categorías puedes anotar las clasificaciones que existen de manera individual y grupal. Finalmente, en cada clasificación, puedes escribir los tipos de deportes que pueden practicarse en las diferentes clasificaciones asignadas:
Por ejemplo, en los deportes individuales encuentras los atléticos como “natación” o los de combate como “boxeo”; mientras que en los deportes de equipo encuentras aquellos que se juegan con pelota como “futbol”, “basquetbol” o “futbol americano”.
Numero 3: Línea del tiempo
Si deseas ordenar cronológicamente procesos o acontecimientos que han ocurrido a lo largo de un período específico como años, lustros, décadas, siglos o milenios, entonces puedes hacer uso del apoyo gráfico denominado línea del tiempo.
Esta herramienta permite comprender cómo se relacionan los hechos, cuál fue su duración y en qué momento se produjeron; observando con claridad la relación temporal que existió entre ellos.
Su elaboración es sencilla, pero requiere que se siga una serie de pasos:
1. Primero debes seleccionar un tema y determinar la fecha inicial y final que representarás.
2. Después debes elegir el periodo que deseas representar. Es importante que utilices una misma medida de tiempo en todo el gráfico.
Por ejemplo: si vas a elaborar una representación de los hechos más importantes de este siglo, la línea del tiempo puede estar dividida en años.
3. Al concluir, debes ubicar los acontecimientos más relevantes en orden cronológico y trazar una línea recta para comenzar a escribir la información en forma de diagrama; las palabras o ideas clave deben ser breves, concretas y suficientes para facilitar su comprensión.
Si la línea recta se traza de forma horizontal los acontecimientos deberán escribirse de izquierda a derecha; si se realiza de forma vertical escribirás de arriba hacia abajo.
También puedes agregar imágenes o dibujos que representen y complementen los datos expuestos; es recomendable utilizar diferentes tipos de líneas o colores para distinguir cada periodo o acontecimiento histórico y ubicar con mayor facilidad los datos en el tiempo.
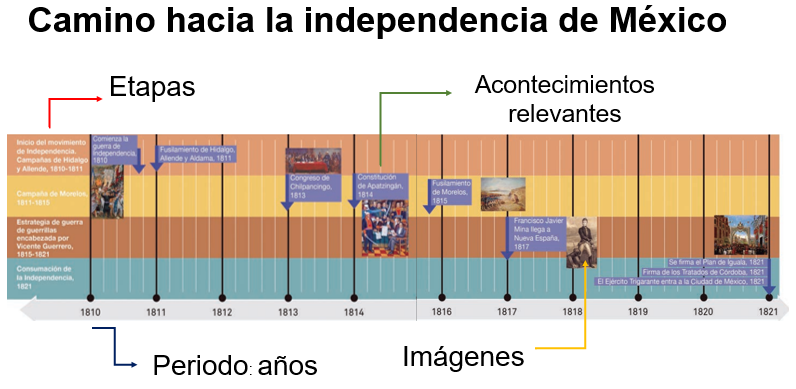
La imagen anterior es un ejemplo de línea de tiempo. En ella, puedes observar el camino hacia la independencia de México, dividido en etapas que se encuentran ubicadas con diferentes colores y utilizando como referencia temporal los años. Puedes ver que a lo largo de la línea se localizan los acontecimientos más relevantes que ocurrieron en cada fase, y está ilustrado con fotografías que complementan y ejemplifican la información expuesta.
Numero 2: Mapa Conceptual
Para crear una sinopsis gráfica de un tema en específico, puedes hacer uso de los mapas conceptuales. El mapa conceptual es un recurso que establece ideas de manera descendente, escritas de forma jerárquica dentro de figuras geométricas como óvalos o recuadros, que se conectan entre sí a través de líneas y palabras de enlace.
Esta técnica obliga a relacionar con el tema y jugar con los conceptos, pues debes organizar y resumir la información de manera correcta, situando el tema central y los términos conceptuales en los recuadros, relacionándolos con palabras de enlace para formar una proposición a través de líneas que logren la unión de dicha idea.
Los elementos que caracterizan este tipo de diagramas son la “jerarquización”, que permite ordenar en grado de importancia los conceptos; la “síntesis”, que incluye únicamente lo más importante del texto; el “impacto visual”, que muestra las relaciones entre las ideas principales de un modo simple y vistoso; las “proporciones”, que permiten identificar fácilmente los conceptos más o menos importantes, con letras de diferentes tamaños escritas en mayúsculas o minúsculas, y el “uso de conectores”, que hará que la interpretación de la información sea adecuada.
Para poder elaborar un mapa conceptual debes “seleccionar” un tema y los conceptos relacionados con dicho texto para enlistarlos, sin repetir términos, “agrupar” los conceptos que se relacionan y “ordenar” las ideas en grado de importancia, partiendo de las generales y finalizando en las específicas. Después, debes “representar” los conceptos en el diagrama y “conectarlos” para comprobar si el tema es comprensible.
Numero 1: Mapa Mental
El mapa mental es un diagrama que sirve para representar información a través de una palabra clave o idea central de forma lógica y creativa, haciendo uso de dibujos, imágenes, palabras clave, signos, símbolos, códigos y colores que transmiten información específica de un tema en particular o de la ramificación de varios temas relacionados con un punto central.
Su elaboración genera apuntes visuales que permiten sintetizar los conocimientos, transmitir el pensamiento y generar el aprendizaje.
Para entender mejor la estructura del mapa mental, imagina el plano de una ciudad: el centro representa la idea principal; las principales avenidas que llevan al centro representan los pensamientos clave del proceso mental; las calles menores representan los pensamientos secundarios y las imágenes, anuncios o nombres de establecimientos ejemplifican ideas especialmente importantes.
Un mapa mental se obtiene y se desarrolla alrededor de una palabra, frase o texto, situado en el centro, seguido de ideas, palabras y conceptos, mediante líneas que se trazan alrededor del título en el sentido de las manecillas del reloj.
Cabe también hacer mención a otros, que son comunes, como las tablas, cuadros comparativos, mapas o diagramas.
Hacer uso de uno u otro organizador depende de la información que quieras presentar y las relaciones que se establecen entre los conceptos. Por ejemplo, ¿podrías hacer una gráfica con la información de los diversos deportes? Probablemente no, ya que no cuentas con cifras. Para representar el desarrollo del periodo conocido como la Paz Armada, ¿qué organizador utilizarías?
Es importante elegir el organizador que mejor presente la información y la relación que se establece entre los conceptos, en función de las fuentes que consultes para la elaboración de tus fichas temáticas.
Retoma el apoyo gráfico que se mencionó como número uno de la lista, y elabora un mapa mental con la información que acabas de aprender.
Te recomendamos realizar la actividad en tu cuaderno; de esta manera podrás sintetizar la información que aprendiste durante la clase y repasar el tema las veces que lo consideres necesario.
Para comenzar debes escribir el tema central de tu mapa: “apoyos gráficos”:
Y realizar la primera ramificación donde escribirás “gráfica de barras” desprendiendo algunos otros conceptos como: datos, categorías, recursos visuales, leyendas para identificar distintos elementos con colores o formas y barras horizontales y verticales; además, incluirás dos imágenes que ejemplifiquen este apoyo gráfico.
En la segunda ramificación colocarás el “cuadro sinóptico” para desglosar conceptos como contenido organizado, semejanzas y diferencias, estructura lógica, ideas clave: generales y particulares, múltiples relaciones, subdivisiones y llaves.
En la tercera ramificación anotaras “línea del tiempo” y subramas que contengan la cronología de procesos o acontecimientos, periodos donde señales los meses, años, lustros, décadas, siglos o milenios, y funciones de las cuales se desprenden comprender hechos, relación temporal y duración de los sucesos. También agregarás una subdivisión que indique la elaboración: seleccionar el tema, determinar la fecha inicial y final, periodo en que se dividirá, ubicación de acontecimientos, orden cronológico y orientación de la línea: horizontal con una escritura de izquierda a derecha o vertical para anotar los datos de arriba hacia abajo; e imágenes o colores que representen y diferencien la información. Para concluir esta ramificación agregarás ilustraciones que muestren distintos ejemplos de líneas del tiempo.
La penúltima ramificación corresponderá al “mapa conceptual” y de esta línea desglosarás otras para colocar sinopsis gráfica, ideas descendentes y jerarquización, síntesis, impacto visual, palabras escritas en óvalos o recuadros, proporciones de letras con mayúsculas o minúsculas y uso de conectores con líneas y palabras de enlace. Además, agregarás los pasos para su elaboración en subdivisiones que contengan las palabras: seleccionar tema y conceptos principales, agrupar ideas, ordenar generales y específicas, representar los conceptos y conectarlos.
Por último, añadirás una ramificación que explique las características del mapa mental, desprendiendo conceptos como: idea central, palabras clave, dibujos, signos, símbolos y códigos de forma lógica y creativa, y ramificaciones en sentido de las manecillas del reloj, con temas relacionados y asociación de ideas. Podrás terminar el diagrama con dibujos que representen la información expuesta.
Al completar todas las ramificaciones y apoyos gráficos que se mencionaron en la lista, tu mapa mental estará terminado. No olvides añadir creatividad a tu trabajo a fin de que adquiera una presentación adecuada y útil para repasar el contenido de la sesión.
Puedes consultar en tu libro de texto los contenidos relacionados con el aprendizaje esperado: “Elabora fichas temáticas con fines de estudio”, y realizar las actividades propuestas para poder afianzar sus conocimientos.
Recuerda que colocar estos apoyos gráficos en tus fichas temáticas te permitirá identificar y distinguir las ideas principales de las secundarias, así como establecer relaciones entre los conceptos. Por ejemplo, puedes utilizar las tablas para comparar datos, los cuadros sinópticos para ordenar información en categorías, las gráficas para representar datos numéricos, y los diagramas para señalar las partes de un objeto o las fases de un proceso.
Observa la siguiente ficha de trabajo realizada por un compañero de secundaria y posteriormente analizarás qué tipo de información presenta y qué organizador gráfico podrías usar.

Comienza con la siguiente pregunta:
¿De qué manera podrías contar brevemente tu historia de vida, colocando las fechas y acontecimientos más importantes de forma cronológica?
Si recuerdas las lecturas de Historia, seguramente habrás podido observar que con frecuencia los sucesos más relevantes ocurridos durante un cierto periodo se presentan de manera concreta y secuencial en una línea de tiempo. Este ejemplo, la línea de tiempo, es un ejemplo de apoyo gráfico.
Un apoyo gráfico es una herramienta que se utiliza para mostrar datos de manera abreviada, con una interpretación fácil, que permite comparar información, ordenar en categorías, representar datos numéricos o lugares específicos en un espacio geográfico y señalar las partes de un objeto o las fases de un proceso. Los cuadros sinópticos, mapas mentales, conceptuales, tablas, gráficas, diagramas o líneas del tiempo forman parte de algunos ejemplos que conforman los diversos apoyos gráficos que existen.
Para conocer más sobre el tema y saber qué son los apoyos gráficos, qué tipos de organizadores existen y para qué se utilizan, observa la siguiente cápsula del minuto 1:22 al 4:41 .
- ¿Cómo leer y construir apoyos gráficos?
https://www.youtube.com/watch?v=GCsX8h-dfpg
Como pudiste observar, las fichas de trabajo son un recurso que permite registrar la información más importante de un tema de forma ordenada. En ocasiones, la información y datos recopilados se pueden presentar mediante una imagen o esquema, con palabras clave que permiten estructurar y sintetizar la información de manera visual, facilitando la comprensión, el análisis y la memoria del texto, al tiempo que se brinda una idea clara del contenido. A estas imágenes y esquemas se les conoce genéricamente como apoyos gráficos.
Sin duda, existe una amplia variedad de apoyos gráficos, compuestos por ideas o conceptos claves e imágenes o dibujos que explican el contenido, resumen la información y facilitan la comprensión del texto.
Para poder elaborar y utilizar los diferentes apoyos gráficos que existen, es necesario conocer los elementos y características que conforman cada uno. Así que a continuación revisarás los 5 organizadores gráficos más comunes.
En tu cuaderno elabora un cuadro comparativo como el que se presenta en la siguiente imagen:

En la primera columna enlista el nombre de los gráficos que se mencionen durante la sesión, seguido de cinco características específicas para cada recurso y finalmente, en la tercera sección, ejemplifica el diagrama con una imagen o dibujo.
Aprenderás sobre los cinco organizadores gráficos más frecuentes.
Número 5: Gráfica de barras
Un diagrama de barras, también conocido como gráfico de barras o columnas, es un elemento que sirve para representar y comparar con un solo golpe de vista un conjunto de datos o valores por categorías mediante recursos visuales. Las barras pueden orientarse horizontal y verticalmente, sin embargo, la altura de cada una será proporcional al número de datos o valores que represente.

Por ejemplo: en esta gráfica se consideran los datos sobre la percepción de la cantidad de imágenes en los libros de texto. Si graficas la percepción sobre la cantidad de imágenes por página, podrás colocar los números obtenidos de forma vertical y las asignaturas de forma horizontal; diferenciándolas por colores, tal como se muestra en el ejemplo. El tamaño de las barras dependerá de los datos, en este caso, de la cantidad de imágenes percibida en los materiales de cada asignatura.

Otra forma de ordenar los datos es orientar las barras de manera vertical. En este ejemplo, los elementos aparecen de forma inversa, es decir, de manera vertical se enlistan todas las asignaturas mientras que de manera horizontal se coloca la cantidad de imágenes percibidas.
En ambos casos puedes agregar leyendas, componentes usados para identificar con mayor claridad los distintos elementos que conforman un gráfico, tales como colores o formas. Para este ejemplo se utilizan colores diferentes para representar cada asignatura.
Numero 4: Cuadro Sinóptico
El cuadro sinóptico es una estrategia que permite organizar y clasificar el contenido de un texto de manera sencilla para expresar visualmente las ideas principales de una temática y sus múltiples relaciones, partiendo del concepto general y dirigiéndolo hacia datos particulares, utilizando llaves para conectar la secuencia de la información, a través de una estructura lógica.
Sirve para contrastar los contenidos, anotando las semejanzas y diferencias, entre una o varias variables de un mismo tema. Pueden utilizarse como estrategias de enseñanza para organizar las ideas que aprendas durante tus clases.
Para elaborar un cuadro sinóptico de manera fácil, puedes dividir el contenido en subtemas y describir estos dentro de subdivisiones o llaves; así los conceptos o palabras claves que utilices estarán clasificados y descritos brevemente, facilitando la comprensión y memorización del tema.
Por ejemplo: si elaboras un cuadro sinóptico de los diferentes deportes que existen, primero puedes colocar el tema central, “deportes”, después puedes agregar dos categorías: los deportes individuales y los deportes que se practican en equipo; posteriormente, en esas categorías puedes anotar las clasificaciones que existen de manera individual y grupal. Finalmente, en cada clasificación, puedes escribir los tipos de deportes que pueden practicarse en las diferentes clasificaciones asignadas:
Por ejemplo, en los deportes individuales encuentras los atléticos como “natación” o los de combate como “boxeo”; mientras que en los deportes de equipo encuentras aquellos que se juegan con pelota como “futbol”, “basquetbol” o “futbol americano”.
Numero 3: Línea del tiempo
Si deseas ordenar cronológicamente procesos o acontecimientos que han ocurrido a lo largo de un período específico como años, lustros, décadas, siglos o milenios, entonces puedes hacer uso del apoyo gráfico denominado línea del tiempo.
Esta herramienta permite comprender cómo se relacionan los hechos, cuál fue su duración y en qué momento se produjeron; observando con claridad la relación temporal que existió entre ellos.
Su elaboración es sencilla, pero requiere que se siga una serie de pasos:
1. Primero debes seleccionar un tema y determinar la fecha inicial y final que representarás.
2. Después debes elegir el periodo que deseas representar. Es importante que utilices una misma medida de tiempo en todo el gráfico.
Por ejemplo: si vas a elaborar una representación de los hechos más importantes de este siglo, la línea del tiempo puede estar dividida en años.
3. Al concluir, debes ubicar los acontecimientos más relevantes en orden cronológico y trazar una línea recta para comenzar a escribir la información en forma de diagrama; las palabras o ideas clave deben ser breves, concretas y suficientes para facilitar su comprensión.
Si la línea recta se traza de forma horizontal los acontecimientos deberán escribirse de izquierda a derecha; si se realiza de forma vertical escribirás de arriba hacia abajo.
También puedes agregar imágenes o dibujos que representen y complementen los datos expuestos; es recomendable utilizar diferentes tipos de líneas o colores para distinguir cada periodo o acontecimiento histórico y ubicar con mayor facilidad los datos en el tiempo.

La imagen anterior es un ejemplo de línea de tiempo. En ella, puedes observar el camino hacia la independencia de México, dividido en etapas que se encuentran ubicadas con diferentes colores y utilizando como referencia temporal los años. Puedes ver que a lo largo de la línea se localizan los acontecimientos más relevantes que ocurrieron en cada fase, y está ilustrado con fotografías que complementan y ejemplifican la información expuesta.
Numero 2: Mapa Conceptual
Para crear una sinopsis gráfica de un tema en específico, puedes hacer uso de los mapas conceptuales. El mapa conceptual es un recurso que establece ideas de manera descendente, escritas de forma jerárquica dentro de figuras geométricas como óvalos o recuadros, que se conectan entre sí a través de líneas y palabras de enlace.
Esta técnica obliga a relacionar con el tema y jugar con los conceptos, pues debes organizar y resumir la información de manera correcta, situando el tema central y los términos conceptuales en los recuadros, relacionándolos con palabras de enlace para formar una proposición a través de líneas que logren la unión de dicha idea.
Los elementos que caracterizan este tipo de diagramas son la “jerarquización”, que permite ordenar en grado de importancia los conceptos; la “síntesis”, que incluye únicamente lo más importante del texto; el “impacto visual”, que muestra las relaciones entre las ideas principales de un modo simple y vistoso; las “proporciones”, que permiten identificar fácilmente los conceptos más o menos importantes, con letras de diferentes tamaños escritas en mayúsculas o minúsculas, y el “uso de conectores”, que hará que la interpretación de la información sea adecuada.
Para poder elaborar un mapa conceptual debes “seleccionar” un tema y los conceptos relacionados con dicho texto para enlistarlos, sin repetir términos, “agrupar” los conceptos que se relacionan y “ordenar” las ideas en grado de importancia, partiendo de las generales y finalizando en las específicas. Después, debes “representar” los conceptos en el diagrama y “conectarlos” para comprobar si el tema es comprensible.
Numero 1: Mapa Mental
El mapa mental es un diagrama que sirve para representar información a través de una palabra clave o idea central de forma lógica y creativa, haciendo uso de dibujos, imágenes, palabras clave, signos, símbolos, códigos y colores que transmiten información específica de un tema en particular o de la ramificación de varios temas relacionados con un punto central.
Su elaboración genera apuntes visuales que permiten sintetizar los conocimientos, transmitir el pensamiento y generar el aprendizaje.
Para entender mejor la estructura del mapa mental, imagina el plano de una ciudad: el centro representa la idea principal; las principales avenidas que llevan al centro representan los pensamientos clave del proceso mental; las calles menores representan los pensamientos secundarios y las imágenes, anuncios o nombres de establecimientos ejemplifican ideas especialmente importantes.
Un mapa mental se obtiene y se desarrolla alrededor de una palabra, frase o texto, situado en el centro, seguido de ideas, palabras y conceptos, mediante líneas que se trazan alrededor del título en el sentido de las manecillas del reloj.
Cabe también hacer mención a otros, que son comunes, como las tablas, cuadros comparativos, mapas o diagramas.
Hacer uso de uno u otro organizador depende de la información que quieras presentar y las relaciones que se establecen entre los conceptos. Por ejemplo, ¿podrías hacer una gráfica con la información de los diversos deportes? Probablemente no, ya que no cuentas con cifras. Para representar el desarrollo del periodo conocido como la Paz Armada, ¿qué organizador utilizarías?
Es importante elegir el organizador que mejor presente la información y la relación que se establece entre los conceptos, en función de las fuentes que consultes para la elaboración de tus fichas temáticas.
Retoma el apoyo gráfico que se mencionó como número uno de la lista, y elabora un mapa mental con la información que acabas de aprender.
Te recomendamos realizar la actividad en tu cuaderno; de esta manera podrás sintetizar la información que aprendiste durante la clase y repasar el tema las veces que lo consideres necesario.
Para comenzar debes escribir el tema central de tu mapa: “apoyos gráficos”:
Y realizar la primera ramificación donde escribirás “gráfica de barras” desprendiendo algunos otros conceptos como: datos, categorías, recursos visuales, leyendas para identificar distintos elementos con colores o formas y barras horizontales y verticales; además, incluirás dos imágenes que ejemplifiquen este apoyo gráfico.
En la segunda ramificación colocarás el “cuadro sinóptico” para desglosar conceptos como contenido organizado, semejanzas y diferencias, estructura lógica, ideas clave: generales y particulares, múltiples relaciones, subdivisiones y llaves.
En la tercera ramificación anotaras “línea del tiempo” y subramas que contengan la cronología de procesos o acontecimientos, periodos donde señales los meses, años, lustros, décadas, siglos o milenios, y funciones de las cuales se desprenden comprender hechos, relación temporal y duración de los sucesos. También agregarás una subdivisión que indique la elaboración: seleccionar el tema, determinar la fecha inicial y final, periodo en que se dividirá, ubicación de acontecimientos, orden cronológico y orientación de la línea: horizontal con una escritura de izquierda a derecha o vertical para anotar los datos de arriba hacia abajo; e imágenes o colores que representen y diferencien la información. Para concluir esta ramificación agregarás ilustraciones que muestren distintos ejemplos de líneas del tiempo.
La penúltima ramificación corresponderá al “mapa conceptual” y de esta línea desglosarás otras para colocar sinopsis gráfica, ideas descendentes y jerarquización, síntesis, impacto visual, palabras escritas en óvalos o recuadros, proporciones de letras con mayúsculas o minúsculas y uso de conectores con líneas y palabras de enlace. Además, agregarás los pasos para su elaboración en subdivisiones que contengan las palabras: seleccionar tema y conceptos principales, agrupar ideas, ordenar generales y específicas, representar los conceptos y conectarlos.
Por último, añadirás una ramificación que explique las características del mapa mental, desprendiendo conceptos como: idea central, palabras clave, dibujos, signos, símbolos y códigos de forma lógica y creativa, y ramificaciones en sentido de las manecillas del reloj, con temas relacionados y asociación de ideas. Podrás terminar el diagrama con dibujos que representen la información expuesta.
Al completar todas las ramificaciones y apoyos gráficos que se mencionaron en la lista, tu mapa mental estará terminado. No olvides añadir creatividad a tu trabajo a fin de que adquiera una presentación adecuada y útil para repasar el contenido de la sesión.
Puedes consultar en tu libro de texto los contenidos relacionados con el aprendizaje esperado: “Elabora fichas temáticas con fines de estudio”, y realizar las actividades propuestas para poder afianzar sus conocimientos.
Recuerda que colocar estos apoyos gráficos en tus fichas temáticas te permitirá identificar y distinguir las ideas principales de las secundarias, así como establecer relaciones entre los conceptos. Por ejemplo, puedes utilizar las tablas para comparar datos, los cuadros sinópticos para ordenar información en categorías, las gráficas para representar datos numéricos, y los diagramas para señalar las partes de un objeto o las fases de un proceso.