MATEMÁTICAS - SECUNDARIA 1
Gráfica circular o de pastel
(LUN 14 DICIEMBRE)
RESUMEN:
Revisa la siguiente situación ya que utilizarás algunos datos para elaborar una gráfica de pastel.
Mi tío Lucas vende aguas en un parque de su colonia, cada lunes va a surtirse de la fruta y los jarabes necesarios para hacer sus preparados. Para evitar excederse en las compras, o bien, comprar lo necesario, realiza un registro de los litros de agua de cada sabor que vende en el día. Por ejemplo, la última ocasión contabilizó 80 litros de agua. Esto también le permite conocer cuáles son los sabores que menos vende y así poder cambiarlos para obtener mayores ganancias. Cada vez que vendía un litro de cierto sabor, colocaba una marca formando grupos de cinco marcas para facilitar su conteo final. Así obtuvo este registro.

Ayuda al tío Lucas a organizar mejor la información del registro que realiza de las ventas del día. ¿Cómo podrías organizar mejor esta información?
Con una tabla de frecuencias; pero para que la información sea más evidente para el tío Lucas, realizaremos una gráfica, en este caso, una gráfica circular o de pastel, éste es un gráfico en donde se delimitan sectores circulares, como si se trataran de rebanadas de un pastel. Pon atención al siguiente video.
- Elementos de una gráfica circular
Del minuto: 1:34 al 2:50
Como observaste en el video, los sectores de una gráfica circular se representan como porcentajes y deben sumar 100%. Para construir una gráfica circular te sugerimos, anotar la información en una tabla de frecuencias como la siguiente:
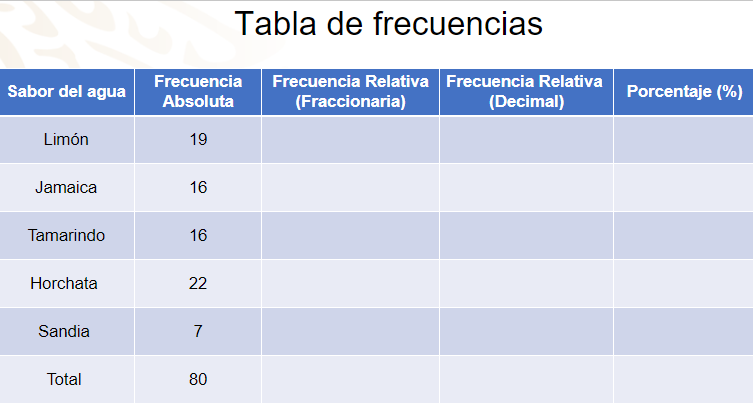
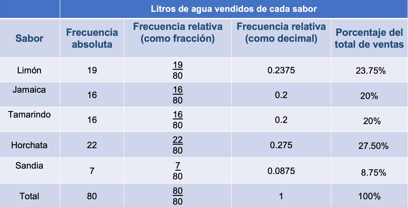
En la primera columna colocamos “sabores de agua” que vendió el tío Lucas, en la segunda columna “frecuencia absoluta” que se refiere al total de litros de agua vendidos de cada sabor; en la tercera columna la “frecuencia relativa” expresada en forma fraccionaria, y que sirve para comparar los litros de agua vendidos de cada sabor y el total de litros vendidos durante el día; en la cuarta, la frecuencia relativa, expresada con número decimal, y en la quinta “porcentaje” de las ventas que representa cada sabor.
En los espacios para anotar los sabores de las aguas, pondremos limón con frecuencia absoluta de 19, abajo Jamaica con 16 de frecuencia absoluta, en la siguiente fila tamarindo y 16 de frecuencia absoluta, posteriormente horchata con 22 de frecuencia, en la siguiente fila sandía con 7 de frecuencia, y en la séptima fila colocamos el total que es la suma de las frecuencias absolutas, que es 80.
Lo primero que calcularemos será la frecuencia relativa que, es el cociente de la frecuencia absoluta de cada dato, entre el total de datos. Por ejemplo, dividiremos los litros de agua que vendió de limón, que son 19, entre el total de litros de agua vendidos de todos los sabores, que son 80. y así sucesivamente para cada sabor.
El total de litros que vendió el tío Lucas en un día, fue de 80 litros. Con este dato podemos calcular la frecuencia relativa del agua de limón; para ello obtendremos el cociente de la frecuencia absoluta, que son los 19 litros, entre el total de litros, que son 80, dándonos como resultado 0.2375. Para el segundo sabor realizaremos lo mismo, encontraremos el cociente de la frecuencia absoluta, que son 16 entre el total de los litros que son 80, que da como resultado 0.2. Para el agua de tamarindo obtenemos el cociente de 16 entre 80 y es 0.2, para la siguiente fila que es el agua de horchata será 22 entre 80, que da como resultado 0.275, y para el último dato el cociente de 7 entre 80 es 0.0875.
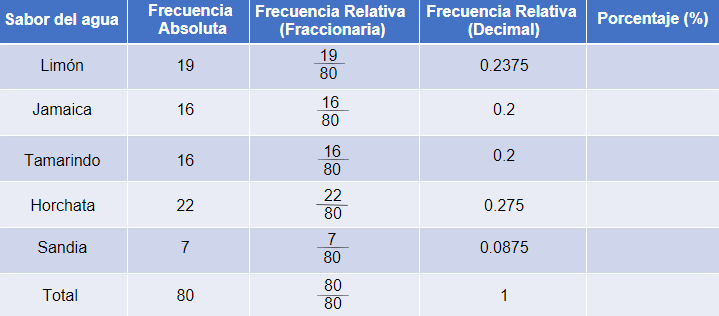
Ya calculamos la frecuencia relativa tanto de manera fraccionaria como decimal. Ahora calcularemos el porcentaje que representa los litros de cada sabor de agua vendida con respecto al total, ya que este dato nos ayudará a construir una gráfica de pastel.
Para eso multiplicaremos cada valor de la frecuencia relativa en número decimal por cien. Comenzaremos con la frecuencia relativa del agua de limón, que es 0.2375 por 100, cuyo producto es 23.75, así que podemos decir que la cantidad de aguas de limón vendidas representan un 23.75 % con respecto al total. Continuamos con el agua de jamaica que es de 0.2 x 100 = 20% de las aguas vendidas corresponde al sabor de jamaica. El agua de tamarindo tiene la misma frecuencia relativa que el agua de jamaica que es de 0.2, así que también representa el 20 por ciento de las ventas. La frecuencia relativa del agua de horchata es de 0.275 x 100 = 27.5 % de las ventas que se tuvieron en ese día corresponden al sabor de horchata. Finalmente, calculemos el porcentaje de aguas vendidas de sandía, si la frecuencia relativa fue de 0.0875, entonces el porcentaje es de 8.75 %.
Ya tenemos todos los datos necesarios para construir una gráfica circular, la cual nos ayudará a mostrarle la información de una manera accesible a mi tío Lucas; y así él podrá analizar, comparar, y visualizar rápidamente la información.
Analiza el siguiente video, que muestra los elementos de este tipo de gráficas, para después continuar con la elaboración de la gráfica.
- Elementos de una gráfica circular
Del minuto: 2:56 a 4:13
Como te pudiste dar cuenta en el video, el sector circular es una parte del área de un círculo que está comprendida entre dos radios. Recuerda que el radio es el segmento de recta que va desde el centro del círculo a la circunferencia y un arco es cierta parte de la circunferencia. Te sugerimos anotar estos elementos del gráfico circular para que los tengas presentes.
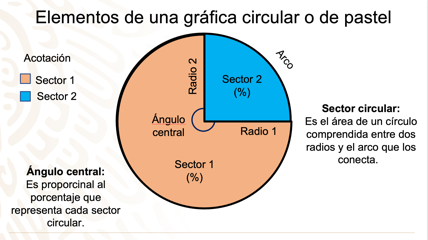
En la imagen se muestra una gráfica circular, con dos radios trazados que delimitan 2 sectores circulares, la parte de la circunferencia que abarca un sector circular se le llama arco y lo puedes ver señalado en la figura. A cada sector le corresponde un ángulo central del círculo, que son proporcionales al porcentaje que representa cada sector circular. ¿Qué otros elementos necesitamos en la tabla para construir un gráfico circular?
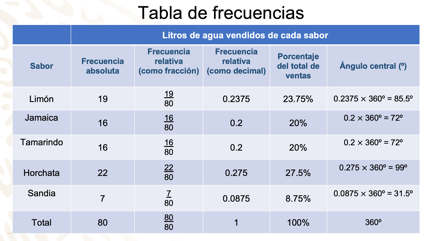
Para construir una gráfica circular, necesitamos conocer la medida del ángulo central que le corresponden a cada uno de los sectores circulares de la gráfica, para ello, agregaremos una columna más a la tabla que llevará como encabezado la palabra “Ángulo central”.
Ahora bien, la medida del ángulo que le corresponde a una vuelta completa delimitando la circunferencia de un círculo es de 360°, tomaremos como base este dato para calcular los ángulos que corresponden al total de aguas vendidas de cada sabor.
Utilizaremos los porcentajes obtenidos para calcular el ángulo de cada sector circular; ya que, ese mismo porcentaje debe ser el de 360º que represente cada ángulo. Para eso multiplicaremos la representación de cada porcentaje como número decimal; es decir, la frecuencia relativa por 360°.
La frecuencia relativa del agua de limón, que es 0.2375 x 360° = 85.5°; para la medida del ángulo del agua de jamaica, 0.2 x 360° = 72°; el agua de tamarindo también tiene una frecuencia relativa de 0.2 que da como producto 72°, la frecuencia relativa del agua de horchata es de 0.275 y si multiplicamos por 360°, tenemos 99°. Ahora, si la frecuencia relativa fue de 0.0875 para el agua de sandía, entonces los grados que le corresponden son 31.5°. Bien, ya hemos calculado los grados que le corresponden a cada uno de los sectores circulares de los sabores de agua, ahora comprobemos que son correctos, para eso debemos sumar las medidas de todos los ángulos y debe dar como resultado 360°, corroboremos, 85.5° + 72° + 72° + 99° + 31.5° es igual a 360°.
Finalmente, para construir la gráfica de pastel, te sugerimos usar tu compás; traza una circunferencia con el radio que gustes.
Ahora, con el agua de limón, colocaremos el centro del transportador en el centro del círculo y el radio, entonces marcamos 85.5° en sentido contrario de las manecillas del reloj, trazamos un segmento recto desde la marca hasta el punto inicial (el centro del círculo), esta sección representa 23.75% que es el porcentaje que le corresponde a los litros de agua de limón vendidos; ahora ubicamos el transportador de manera que tomaremos como base el primer radio y marcaremos un ángulo de 72° en sentido contrario a las manecillas del reloj, trazamos un segmento recto desde la marca hasta el punto inicial, este sector representa el 20%, que corresponde a los litros vendidos, de agua de jamaica. Seguimos el mismo procedimiento para los litros de agua de tamarindo, marcamos y trazamos un ángulo de 72°, adyacente al anterior, que representa 20% que son los litros de agua de tamarindo vendidos. Haremos el mismo procedimiento para localizar los siguientes ángulos, 99° representa el 27.5% que es la cantidad de aguas de horchata vendidas. Ahora ubicamos a 31.5° que representa el 8.75% que es la cantidad de aguas de sandía vendidas.
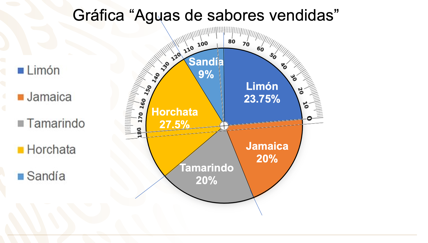
Listo, ya hemos terminado la gráfica circular, y ahora el tío Lucas podrá analizar, comparar y visualizar rápida y sencillamente esta información.
Anota y responde las siguientes preguntas con base en la gráfica:
¿Cuáles son los sabores que menos vende?
El agua que menos vende es la de sandía, por lo que le podemos sugerir cambiar este sabor.
¿Cuáles son los sabores que más vende?
El agua de horchata, ya que es la que tiene un sector más grande, o bien un porcentaje mayor; le sigue el agua de limón.
¿Qué sabores deberá mantener a la venta?
Para continuar con las ventas, y asegurarse de tener ganancias, debería mantener el agua de horchata, limón, jamaica y tamarindo.
Siguiendo con el tema de estudio; como sabes, el INEGI es un organismo público responsable de normar y coordinar el sistema Nacional de Información estadística y Geografía, también capta y difunde información de México que nos permite conocer las características de nuestro país. En su página puedes encontrar muchísima información de utilidad, como la información del censo de población y vivienda que se realiza cada 10 años en todo el territorio nacional.
Una de las encuestas que realizan es para conocer el nivel educativo de la población con 15 o más años de edad. Analiza la siguiente tabla:
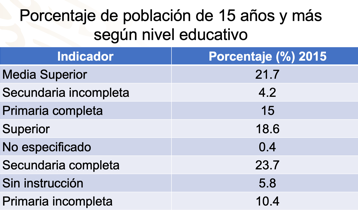
Observa que la tabla muestra el nivel educativo de la población con 15 años de edad, o más, en México en 2015, representada como porcentaje. Observa que el 21.7% de la población mayor de 15 años de edad, cuenta con estudios de nivel Media superior; Secundaria incompleta corresponde al 4.2%; Primaria completa 15 %; nivel superior 18.6%; las personas que no especificaron su nivel educacional 0.4% de la población; secundaria completa 23.7 %; sin instrucción 5.8% y primaria incompleta 10.4%.
Para poder visualizar la información de forma más eficiente tracemos una gráfica circular. Puedes observar en los datos, que ya están dados en porcentajes; por lo tanto, en esta ocasión no será necesario construir la tabla en la que incluimos las columnas de frecuencia absoluta, frecuencia relativa fraccionaria y frecuencia relativa decimal, quedando así directamente, la tabla con el porcentaje.
Vaciaremos los datos en la siguiente tabla de 3 columnas, para que una vez que obtengamos cada valor del ángulo que le corresponde a cada dato, concentremos los datos y así podamos construir fácilmente la gráfica circular.
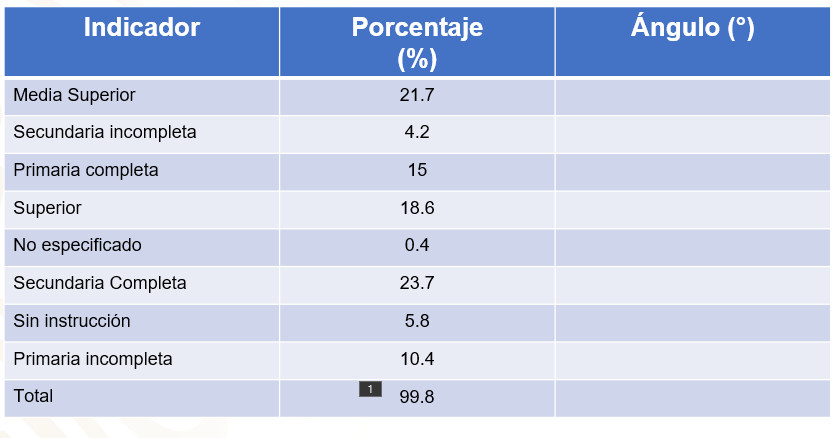
A la tabla le agregamos una columna para representar la medida del ángulo central en cada caso. Ahora sumamos todos los datos para obtener el total que en este caso es de 99.8%.
La suma no llegó al 100% porque hay muchos casos en donde en las tablas de frecuencias, al momento de obtener las frecuencias relativas, obtenemos datos con gran cantidad de decimales, que terminamos redondeando o bien truncando para poder manejarlos de forma más sencilla. Éste es uno de esos casos, lo más importante es fijar la atención en que, en este total la diferencia con 100% no es muy grande, como puedes observar en el ejemplo 99.8%, por ello, consideramos que sí se cubre el 100% que se requiere para construir una gráfica circular.
Para poder completar la columna correspondiente a la medida de los ángulos, como lo hicimos en el caso anterior, multiplicamos 360 grados por la representación del porcentaje como número decimal. Por ejemplo, cuando calculamos 10% de una cantidad, basta con multiplicar la cantidad por 0.1.
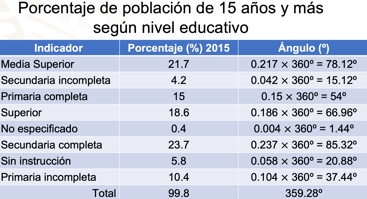
En la primera fila, el porcentaje es 21.7%, y como su representación como número decimal es 0.217, multiplicamos 360° x 0.217 = 78.12°; En la siguiente fila, el porcentaje es 4.2%, entonces multiplicamos 0.042 x 360 = 15.12°; Para la tercera fila tenemos el 15%, entonces, multiplicamos 0.15 x 360° = 54°; En la cuarta fila el porcentaje es 18.6, al multiplicar 0.816 x 360 = 66.96°; En la quinta fila el valor es 0.4%, multiplicamos 0.004 x 360° = 1.44°; La sexta fila con el 23.7%, al multiplicar resulta un ángulo de 85.32°; La séptima con 5.8% da como resultado un ángulo de 20.88°; Y en la octava con 10.4%, al realizar las operaciones obtenemos el ángulo de 37.44°.
Ahora que ya tenemos los ángulos, procedemos a construir la gráfica circular, ten en cuenta que primero debemos trazar la circunferencia preferentemente con compás.
Para construir la gráfica, seguimos el mismo procedimiento que usamos en el problema anterior, trazamos ángulos adyacentes de acuerdo con las medidas que obtuvimos y que registramos en la tabla de datos. Por las medidas obtenidas, redondearemos la medida de los ángulos correspondientes.
Marcamos un ángulo de 78° con el transportador, obteniendo el sector del primer indicador referente al nivel educativo media superior con 21.7%. Enseguida trazamos un ángulo de 15° para el sector de la secundaria incompleta con el 4.2%. Para primaria completa, el ángulo es de 54°, que corresponde al 15%. Un ángulo de 67° le corresponde a educación superior, que representa 18.6%. El quinto dato es no especificó con 0.4% y el ángulo que le corresponde es de 1.5º. Después marcamos 86° que corresponde al 23.7% del nivel educativo secundaria completa. Ahora trazamos un ángulo de 21° correspondiente a 5.8% referente al indicador sin instrucción y por último, el ángulo de 37.5° que queda, corresponde al sector de primaria incompleta con un 10.4.
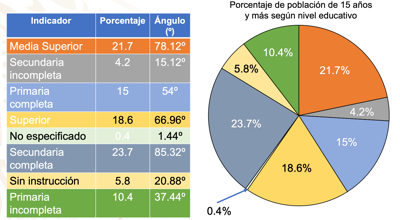
¿Qué tipo de información podríamos obtener de esta gráfica?
Podríamos preguntarnos, por ejemplo: ¿Cuál es el nivel educativo en el que se encuentra un mayor porcentaje de la población mayor a 15 años de edad? O incluso preguntas como ¿Qué tipo de educación tiene mayor cantidad de individuos con más de 15 años edad, la educación básica o la educación media y superior?
También podemos observar que hay una mayor cantidad de personas mayores a quince años de edad, que tienen la primaria incompleta, en comparación con la secundaria incompleta, esto podría orientar acciones para implementar campañas en las primarias y así lograr que cada vez haya menos deserción y que más personas concluyan este nivel educativo.
Los gráficos circulares nos ayudan a representar un conjunto de datos que estén relacionados entre sí, que estén representados como porcentaje, esto facilita el análisis y la comprensión de los mismos, como lo viste en los ejemplos anteriores gracias a esta representación se pueden tomar decisiones, como la realización de campañas para evitar la deserción escolar, para que cada vez más personas concluyan sus estudios, o para realizar estudios en donde se pueda determinar porque un producto se vende con mayor frecuencia que otros.
También las gráficas circulares se utilizan en otras áreas de estudio como la medicina, la economía, el medio ambiente, entre otros aspectos más de la vida cotidiana. Consulta en tu libro de texto el tema de gráficas circulares, verás que hay situaciones interesantes que podrás resolver como las que revisaste en esta sesión.
Revisa la siguiente situación ya que utilizarás algunos datos para elaborar una gráfica de pastel.
Mi tío Lucas vende aguas en un parque de su colonia, cada lunes va a surtirse de la fruta y los jarabes necesarios para hacer sus preparados. Para evitar excederse en las compras, o bien, comprar lo necesario, realiza un registro de los litros de agua de cada sabor que vende en el día. Por ejemplo, la última ocasión contabilizó 80 litros de agua. Esto también le permite conocer cuáles son los sabores que menos vende y así poder cambiarlos para obtener mayores ganancias. Cada vez que vendía un litro de cierto sabor, colocaba una marca formando grupos de cinco marcas para facilitar su conteo final. Así obtuvo este registro.

Ayuda al tío Lucas a organizar mejor la información del registro que realiza de las ventas del día. ¿Cómo podrías organizar mejor esta información?
Con una tabla de frecuencias; pero para que la información sea más evidente para el tío Lucas, realizaremos una gráfica, en este caso, una gráfica circular o de pastel, éste es un gráfico en donde se delimitan sectores circulares, como si se trataran de rebanadas de un pastel. Pon atención al siguiente video.
- Elementos de una gráfica circular
Del minuto: 1:34 al 2:50
Como observaste en el video, los sectores de una gráfica circular se representan como porcentajes y deben sumar 100%. Para construir una gráfica circular te sugerimos, anotar la información en una tabla de frecuencias como la siguiente:

En la primera columna colocamos “sabores de agua” que vendió el tío Lucas, en la segunda columna “frecuencia absoluta” que se refiere al total de litros de agua vendidos de cada sabor; en la tercera columna la “frecuencia relativa” expresada en forma fraccionaria, y que sirve para comparar los litros de agua vendidos de cada sabor y el total de litros vendidos durante el día; en la cuarta, la frecuencia relativa, expresada con número decimal, y en la quinta “porcentaje” de las ventas que representa cada sabor.
En los espacios para anotar los sabores de las aguas, pondremos limón con frecuencia absoluta de 19, abajo Jamaica con 16 de frecuencia absoluta, en la siguiente fila tamarindo y 16 de frecuencia absoluta, posteriormente horchata con 22 de frecuencia, en la siguiente fila sandía con 7 de frecuencia, y en la séptima fila colocamos el total que es la suma de las frecuencias absolutas, que es 80.
Lo primero que calcularemos será la frecuencia relativa que, es el cociente de la frecuencia absoluta de cada dato, entre el total de datos. Por ejemplo, dividiremos los litros de agua que vendió de limón, que son 19, entre el total de litros de agua vendidos de todos los sabores, que son 80. y así sucesivamente para cada sabor.
El total de litros que vendió el tío Lucas en un día, fue de 80 litros. Con este dato podemos calcular la frecuencia relativa del agua de limón; para ello obtendremos el cociente de la frecuencia absoluta, que son los 19 litros, entre el total de litros, que son 80, dándonos como resultado 0.2375. Para el segundo sabor realizaremos lo mismo, encontraremos el cociente de la frecuencia absoluta, que son 16 entre el total de los litros que son 80, que da como resultado 0.2. Para el agua de tamarindo obtenemos el cociente de 16 entre 80 y es 0.2, para la siguiente fila que es el agua de horchata será 22 entre 80, que da como resultado 0.275, y para el último dato el cociente de 7 entre 80 es 0.0875.

Ya calculamos la frecuencia relativa tanto de manera fraccionaria como decimal. Ahora calcularemos el porcentaje que representa los litros de cada sabor de agua vendida con respecto al total, ya que este dato nos ayudará a construir una gráfica de pastel.
Para eso multiplicaremos cada valor de la frecuencia relativa en número decimal por cien. Comenzaremos con la frecuencia relativa del agua de limón, que es 0.2375 por 100, cuyo producto es 23.75, así que podemos decir que la cantidad de aguas de limón vendidas representan un 23.75 % con respecto al total. Continuamos con el agua de jamaica que es de 0.2 x 100 = 20% de las aguas vendidas corresponde al sabor de jamaica. El agua de tamarindo tiene la misma frecuencia relativa que el agua de jamaica que es de 0.2, así que también representa el 20 por ciento de las ventas. La frecuencia relativa del agua de horchata es de 0.275 x 100 = 27.5 % de las ventas que se tuvieron en ese día corresponden al sabor de horchata. Finalmente, calculemos el porcentaje de aguas vendidas de sandía, si la frecuencia relativa fue de 0.0875, entonces el porcentaje es de 8.75 %.
Ya tenemos todos los datos necesarios para construir una gráfica circular, la cual nos ayudará a mostrarle la información de una manera accesible a mi tío Lucas; y así él podrá analizar, comparar, y visualizar rápidamente la información.

Analiza el siguiente video, que muestra los elementos de este tipo de gráficas, para después continuar con la elaboración de la gráfica.
- Elementos de una gráfica circular
Del minuto: 2:56 a 4:13
Como te pudiste dar cuenta en el video, el sector circular es una parte del área de un círculo que está comprendida entre dos radios. Recuerda que el radio es el segmento de recta que va desde el centro del círculo a la circunferencia y un arco es cierta parte de la circunferencia. Te sugerimos anotar estos elementos del gráfico circular para que los tengas presentes.

En la imagen se muestra una gráfica circular, con dos radios trazados que delimitan 2 sectores circulares, la parte de la circunferencia que abarca un sector circular se le llama arco y lo puedes ver señalado en la figura. A cada sector le corresponde un ángulo central del círculo, que son proporcionales al porcentaje que representa cada sector circular. ¿Qué otros elementos necesitamos en la tabla para construir un gráfico circular?
Para construir una gráfica circular, necesitamos conocer la medida del ángulo central que le corresponden a cada uno de los sectores circulares de la gráfica, para ello, agregaremos una columna más a la tabla que llevará como encabezado la palabra “Ángulo central”.
Ahora bien, la medida del ángulo que le corresponde a una vuelta completa delimitando la circunferencia de un círculo es de 360°, tomaremos como base este dato para calcular los ángulos que corresponden al total de aguas vendidas de cada sabor.
Utilizaremos los porcentajes obtenidos para calcular el ángulo de cada sector circular; ya que, ese mismo porcentaje debe ser el de 360º que represente cada ángulo. Para eso multiplicaremos la representación de cada porcentaje como número decimal; es decir, la frecuencia relativa por 360°.
La frecuencia relativa del agua de limón, que es 0.2375 x 360° = 85.5°; para la medida del ángulo del agua de jamaica, 0.2 x 360° = 72°; el agua de tamarindo también tiene una frecuencia relativa de 0.2 que da como producto 72°, la frecuencia relativa del agua de horchata es de 0.275 y si multiplicamos por 360°, tenemos 99°. Ahora, si la frecuencia relativa fue de 0.0875 para el agua de sandía, entonces los grados que le corresponden son 31.5°. Bien, ya hemos calculado los grados que le corresponden a cada uno de los sectores circulares de los sabores de agua, ahora comprobemos que son correctos, para eso debemos sumar las medidas de todos los ángulos y debe dar como resultado 360°, corroboremos, 85.5° + 72° + 72° + 99° + 31.5° es igual a 360°.

Finalmente, para construir la gráfica de pastel, te sugerimos usar tu compás; traza una circunferencia con el radio que gustes.
Ahora, con el agua de limón, colocaremos el centro del transportador en el centro del círculo y el radio, entonces marcamos 85.5° en sentido contrario de las manecillas del reloj, trazamos un segmento recto desde la marca hasta el punto inicial (el centro del círculo), esta sección representa 23.75% que es el porcentaje que le corresponde a los litros de agua de limón vendidos; ahora ubicamos el transportador de manera que tomaremos como base el primer radio y marcaremos un ángulo de 72° en sentido contrario a las manecillas del reloj, trazamos un segmento recto desde la marca hasta el punto inicial, este sector representa el 20%, que corresponde a los litros vendidos, de agua de jamaica. Seguimos el mismo procedimiento para los litros de agua de tamarindo, marcamos y trazamos un ángulo de 72°, adyacente al anterior, que representa 20% que son los litros de agua de tamarindo vendidos. Haremos el mismo procedimiento para localizar los siguientes ángulos, 99° representa el 27.5% que es la cantidad de aguas de horchata vendidas. Ahora ubicamos a 31.5° que representa el 8.75% que es la cantidad de aguas de sandía vendidas.

Listo, ya hemos terminado la gráfica circular, y ahora el tío Lucas podrá analizar, comparar y visualizar rápida y sencillamente esta información.
Anota y responde las siguientes preguntas con base en la gráfica:
¿Cuáles son los sabores que menos vende?
El agua que menos vende es la de sandía, por lo que le podemos sugerir cambiar este sabor.
¿Cuáles son los sabores que más vende?
El agua de horchata, ya que es la que tiene un sector más grande, o bien un porcentaje mayor; le sigue el agua de limón.
¿Qué sabores deberá mantener a la venta?
Para continuar con las ventas, y asegurarse de tener ganancias, debería mantener el agua de horchata, limón, jamaica y tamarindo.
Siguiendo con el tema de estudio; como sabes, el INEGI es un organismo público responsable de normar y coordinar el sistema Nacional de Información estadística y Geografía, también capta y difunde información de México que nos permite conocer las características de nuestro país. En su página puedes encontrar muchísima información de utilidad, como la información del censo de población y vivienda que se realiza cada 10 años en todo el territorio nacional.
Una de las encuestas que realizan es para conocer el nivel educativo de la población con 15 o más años de edad. Analiza la siguiente tabla:

Observa que la tabla muestra el nivel educativo de la población con 15 años de edad, o más, en México en 2015, representada como porcentaje. Observa que el 21.7% de la población mayor de 15 años de edad, cuenta con estudios de nivel Media superior; Secundaria incompleta corresponde al 4.2%; Primaria completa 15 %; nivel superior 18.6%; las personas que no especificaron su nivel educacional 0.4% de la población; secundaria completa 23.7 %; sin instrucción 5.8% y primaria incompleta 10.4%.
Para poder visualizar la información de forma más eficiente tracemos una gráfica circular. Puedes observar en los datos, que ya están dados en porcentajes; por lo tanto, en esta ocasión no será necesario construir la tabla en la que incluimos las columnas de frecuencia absoluta, frecuencia relativa fraccionaria y frecuencia relativa decimal, quedando así directamente, la tabla con el porcentaje.
Vaciaremos los datos en la siguiente tabla de 3 columnas, para que una vez que obtengamos cada valor del ángulo que le corresponde a cada dato, concentremos los datos y así podamos construir fácilmente la gráfica circular.

A la tabla le agregamos una columna para representar la medida del ángulo central en cada caso. Ahora sumamos todos los datos para obtener el total que en este caso es de 99.8%.
La suma no llegó al 100% porque hay muchos casos en donde en las tablas de frecuencias, al momento de obtener las frecuencias relativas, obtenemos datos con gran cantidad de decimales, que terminamos redondeando o bien truncando para poder manejarlos de forma más sencilla. Éste es uno de esos casos, lo más importante es fijar la atención en que, en este total la diferencia con 100% no es muy grande, como puedes observar en el ejemplo 99.8%, por ello, consideramos que sí se cubre el 100% que se requiere para construir una gráfica circular.
Para poder completar la columna correspondiente a la medida de los ángulos, como lo hicimos en el caso anterior, multiplicamos 360 grados por la representación del porcentaje como número decimal. Por ejemplo, cuando calculamos 10% de una cantidad, basta con multiplicar la cantidad por 0.1.

En la primera fila, el porcentaje es 21.7%, y como su representación como número decimal es 0.217, multiplicamos 360° x 0.217 = 78.12°; En la siguiente fila, el porcentaje es 4.2%, entonces multiplicamos 0.042 x 360 = 15.12°; Para la tercera fila tenemos el 15%, entonces, multiplicamos 0.15 x 360° = 54°; En la cuarta fila el porcentaje es 18.6, al multiplicar 0.816 x 360 = 66.96°; En la quinta fila el valor es 0.4%, multiplicamos 0.004 x 360° = 1.44°; La sexta fila con el 23.7%, al multiplicar resulta un ángulo de 85.32°; La séptima con 5.8% da como resultado un ángulo de 20.88°; Y en la octava con 10.4%, al realizar las operaciones obtenemos el ángulo de 37.44°.
Ahora que ya tenemos los ángulos, procedemos a construir la gráfica circular, ten en cuenta que primero debemos trazar la circunferencia preferentemente con compás.
Para construir la gráfica, seguimos el mismo procedimiento que usamos en el problema anterior, trazamos ángulos adyacentes de acuerdo con las medidas que obtuvimos y que registramos en la tabla de datos. Por las medidas obtenidas, redondearemos la medida de los ángulos correspondientes.
Marcamos un ángulo de 78° con el transportador, obteniendo el sector del primer indicador referente al nivel educativo media superior con 21.7%. Enseguida trazamos un ángulo de 15° para el sector de la secundaria incompleta con el 4.2%. Para primaria completa, el ángulo es de 54°, que corresponde al 15%. Un ángulo de 67° le corresponde a educación superior, que representa 18.6%. El quinto dato es no especificó con 0.4% y el ángulo que le corresponde es de 1.5º. Después marcamos 86° que corresponde al 23.7% del nivel educativo secundaria completa. Ahora trazamos un ángulo de 21° correspondiente a 5.8% referente al indicador sin instrucción y por último, el ángulo de 37.5° que queda, corresponde al sector de primaria incompleta con un 10.4.

¿Qué tipo de información podríamos obtener de esta gráfica?
Podríamos preguntarnos, por ejemplo: ¿Cuál es el nivel educativo en el que se encuentra un mayor porcentaje de la población mayor a 15 años de edad? O incluso preguntas como ¿Qué tipo de educación tiene mayor cantidad de individuos con más de 15 años edad, la educación básica o la educación media y superior?
También podemos observar que hay una mayor cantidad de personas mayores a quince años de edad, que tienen la primaria incompleta, en comparación con la secundaria incompleta, esto podría orientar acciones para implementar campañas en las primarias y así lograr que cada vez haya menos deserción y que más personas concluyan este nivel educativo.
Los gráficos circulares nos ayudan a representar un conjunto de datos que estén relacionados entre sí, que estén representados como porcentaje, esto facilita el análisis y la comprensión de los mismos, como lo viste en los ejemplos anteriores gracias a esta representación se pueden tomar decisiones, como la realización de campañas para evitar la deserción escolar, para que cada vez más personas concluyan sus estudios, o para realizar estudios en donde se pueda determinar porque un producto se vende con mayor frecuencia que otros.
También las gráficas circulares se utilizan en otras áreas de estudio como la medicina, la economía, el medio ambiente, entre otros aspectos más de la vida cotidiana. Consulta en tu libro de texto el tema de gráficas circulares, verás que hay situaciones interesantes que podrás resolver como las que revisaste en esta sesión.