MATEMÁTICAS - SECUNDARIA 3
Ecuaciones de segundo grado
(MAR 15 DICIEMBRE)
ACTIVIDAD:
Explora tu libro de texto para buscar los ejercicios correspondientes a este tema y consolida tus conocimientos.
Lee la siguiente apostilla de Albert Einstein.
“¿Cómo es posible que la matemática, un producto del pensamiento humano independiente de la experiencia, se adapte admirablemente a los objetos de la realidad?”
RESUMEN:
Inicia resolviendo algunos problemas en donde apliques procesos de solución de las ecuaciones de segundo grado o cuadráticas.
Observa la primera situación:
Situación 1
- Audiovisual 1 “El corral”

Analiza la primera pregunta:

Se trata de calcular los lados de un rectángulo del que ya se conoces su área, 104m^2, y existe una relación entre el ancho y el largo: uno es mayor que el otro por 5 unidades.
Es decir, el área que es igual al ancho por el largo es igual a 104m^2.
Sea “x” el ancho y “x+5”, el largo. Entonces, el área es igual a “x(x+5)”, que es igual a 104.
Esta es la ecuación algebraica que representa la situación.
La segunda pregunta dice:

Para resolver este tipo de ecuaciones, primero igualas a cero la ecuación.
En este caso, significa restar en ambos lados de la igualdad 104.
Y queda: x^2+5x-104 es igual a 104-104
Queda: x^2 +5x-104 es igual a 0
Esta ecuación se resuelve buscando el término común a dos binomios, que es “x”, y para formar los dos binomios se deben encontrar dos números que multiplicados den “-104”, y que sumados den 5.

Los números que multiplicados dan 104 son 2 y 52, 4 y 26, 8 y 13.
De éstos, se tiene que 52-2 es igual a 50, 26-4 es igual a 22 y 13 – 8 es igual a 5.
Ya tienes los dos números de los binomios: 13 y (-8), que multiplicados dan “-104”.
Así: ð‘¥^2+5ð‘¥−104=(ð‘¥+13)(ð‘¥−8)

De los dos binomios, se tiene que:
(ð‘¥+13)(ð‘¥−8) es igual a 0
Esto implica que alguno de los binomios o los dos son iguales a cero.
Si x+13 es igual a 0, entonces “x” es igual a -13.
Si x-8 es igual a 0, entonces “x” es igual a 8.
Y tienes dos soluciones para “x”: -13 y 8.
Responde la tercera pregunta: ¿cuánto debe medir el ancho y largo del corral?
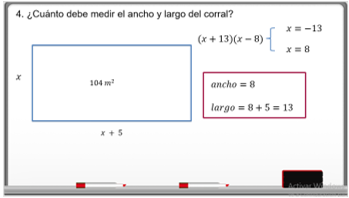
Ya tienes que de (ð‘¥+13) (ð‘¥−8) = 0, hay dos soluciones y eliges la positiva, que es 8.
Se designó a “x” como el ancho, entonces, de ancho tiene 8 metros. El largo es “x+5”, así que 8+5 es igual a 13.
Las medidas son 8 m de ancho, 13 m de largo.
Has podido ayudar a Janet a resolver su problema.
Situación 2
- Audiovisual 2 “El poema cuadrático”

Has encontrado la situación del poema como una ecuación.
La segunda pregunta dice:

Se tiene que:
8(ð‘¥−1)(ð‘¥+1) = ð‘¥−8
Ahora, (ð‘¥−1)(ð‘¥+1) son binomios conjugados, lo que lleva a una diferencia de cuadrados.
Así, (ð‘¥−1)(ð‘¥+1) es igual a x^2-1^2, lo que hace que la ecuación w3q
8(ð‘¥^2−1^2) es igual a ð‘¥−8
8(ð‘¥^2−1) es igual a ð‘¥−8
Y ð‘¥^2−8 es igual a ð‘¥−8
Se resta 8 de ambos lados de la igualdad y queda: 8ð‘¥^2 es igual a ð‘¥
Ahora se divide entre x ambos lados del signo igual, (8ð‘¥^2)/ð‘¥ es igual a ð‘¥/ð‘¥. Como x^2 es igual a “x por x”, 8ð‘¥ð‘¥/ð‘¥ es igual a ð‘¥/ð‘¥, y una cantidad dividida entre sí misma es igual a uno, en este caso x/x es igual a uno.
Así: 8ð‘¥(uno) es igual a uno. Se divide entre 8 ambos lados de la igualdad. Queda:
8ð‘¥/8 es igual a 1/8
Por lo tanto, x es igual a 1/8.
Ya se tiene el valor de “x”.
La tercera pregunta dice:

Comprueba que es 1/8.
En las dos ecuaciones que obtuviste del poema, se sustituirá el valor encontrado, 1/8.
En 8(ð‘¥−1)(ð‘¥+1) y en x-8 se sustituirá “x” por 1/8.
Al sustituir 1/8 en 8(ð‘¥−1)(ð‘¥+1), se tiene: (1/8−1)(1/8+1) es igual a 8(1/8−8/8)(1/8+8/8)
Esto es igual a:
8 por (1−8)/8)(1+8)/8) es igual a = 8 por (−7)/8)(9/8), que es igual a 8 por(−7)(9))/(8)(8)
Al multiplicar (-7)(9) es igual a -63, y se multiplica una vez por 8 y se divide dos veces entre 8, así que es igual a -63/8.
Al sustituir 1/8 en x-8, se tiene que 1/8−64/8, ya que 64/8 es igual a 8.
1/8−64/8 es igual a (1-64)/8, es igual a -63/8
Por las dos expresiones generadas por el poema, se ha visto que “x” es igual a 1/8.
Situación 3
Como tercera situación, una alumna expone su problema, observa en qué le puedes ayudar.

La primera pregunta es:
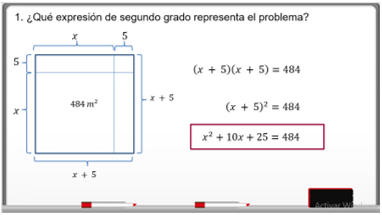
Es un problema de área de un cuadrado en el que se conoce el área resultante: 484 metros cuadrados, y la medida del lado, (x+5).
El área del cuadrado es (x+5)^2, es igual a 484.
Desarrollando el cuadrado queda:
ð‘¥^2+10ð‘¥+25=484
Esta expresión algebraica representa al problema.
La segunda pregunta dice:
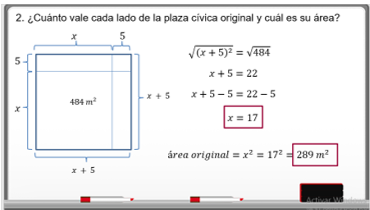
Para contestar esta pregunta, debes conocer el valor de “x”. Para esto, se ocupará la ecuación:
(ð‘¥ + 5)^2 es igual a 484
Para despejar “x”, hay que obtener la raíz cuadrada de cada lado de la igualdad.
La raíz cuadrada de (x+5)^2 es igual a x+5; la raíz cuadrada de 484 es 22.
Queda:
x+5 es igual a 22
Se resta 5 a cada lado de signo igual.
X+5-5 es igual a 22-5
Así, x es igual a 17
Ahora que tienes el valor de “x”, se puede obtener el área original, que es “x” al cuadrado, que es 17 al cuadrado, que es igual a 289 metros cuadrados.
La tercera pegunta es:

Ya se obtuvo el valor cuando se calculó la raíz cuadrada de 484. Resultado: 22 metros por lado.
Otra forma es ocupando el valor encontrado original, “x”, al que se le agregan 5 metros por lado, y queda igual la cantidad de 22 metros por lado.
Situación 4
- Audiovisual “El maíz”

La primera pregunta es:

Es un terreno cuadrado, donde se conoce el área total.
El lado “x” al cuadrado es igual a 1 225.
Entonces, la ecuación cuadrática que responde a esta pregunta es:
x^2 es igual a 1 225
La segunda pregunta dice:
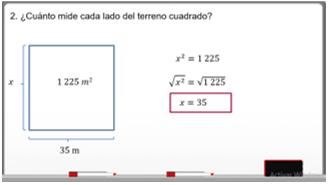
Si se tiene que x^2 es igual a 1 225, entonces se aplica la raíz cuadrada a ambos lados de la igualdad.
Queda: raíz cuadrada de x^2 es igual a la raíz cuadrada de 1 225.
Así, x es igual a 35.
La tercera pregunta es:

Si se tienen 35 metros por lado y se debe sembrar cada planta de maíz cada 2 metros, entonces, por lado, se siembra 35 entre 2, que es igual a 17.
En total, se pueden sembrar (17)(17) igual a 289 plantas de maíz.
Realiza dos preguntas con respecto a las situaciones consideradas.
Selecciona y escribe a qué situación corresponde cada una de las representaciones geométricas.
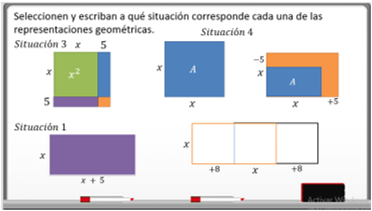
La situación 1 se puede representar por el rectángulo de ancho “x” y largo “x+5”. Y a su lado se escribe: “Situación 1”.
La situación 2, el poema, no tiene representación aquí, así que no se escribe.
La situación 3 está representada por la primera figura, el cuadrado con lados x+5. Se escribe: “Situación 3”.
La situación 4 está representada por la segunda figura geométrica, el cuadrado de lado “x”. Se escribe: “Situación 4”.
Ahora resuelve la siguiente pregunta.
Relaciona las columnas correspondientes anotando en el paréntesis que corresponda a la ecuación correcta y su situación 1, 2, 3 o 4.

La primera situación, la del corral, en donde el largo mide 5 metros más que el ancho y su área es de 104 metros cuadrados, corresponde a x(x+5) es igual a 104. Se escribe: “Situación 1”.
La segunda situación, el del poema, donde se multiplican 8 veces el sucesor con el antecesor y es igual a la cantidad desconocida menos 6, corresponde a 8((ð‘¥+1)(ð‘¥−1)) igual a ð‘¥−8x(x+5). Se escribe: “Situación 2”.
La tercera situación, la de la plaza cívica, donde se aumentó en 5 metros por lado a la plaza original cuadrada, conociendo que el área final es de 484 metros cuadrados, corresponde a (ð‘¥+5)(ð‘¥+5) es igual a 484. Se escribe: “Situación 3”.
La cuarta situación, en donde se busca lo que mide el lado de un terreno cuadrado de área igual a 1 225 metros cuadrados, corresponde a ð‘¥^2=1225.
En esta sesión aprendiste la solución de problemas reales aplicando las ecuaciones de segundo grado y resolviéndolas con diferentes procesos de solución.
Explora tu libro de texto para buscar los ejercicios correspondientes a este tema y consolida tus conocimientos.
Lee la siguiente apostilla de Albert Einstein.
“¿Cómo es posible que la matemática, un producto del pensamiento humano independiente de la experiencia, se adapte admirablemente a los objetos de la realidad?”
Inicia resolviendo algunos problemas en donde apliques procesos de solución de las ecuaciones de segundo grado o cuadráticas.
Observa la primera situación:
Situación 1
- Audiovisual 1 “El corral”

Analiza la primera pregunta:

Se trata de calcular los lados de un rectángulo del que ya se conoces su área, 104m^2, y existe una relación entre el ancho y el largo: uno es mayor que el otro por 5 unidades.
Es decir, el área que es igual al ancho por el largo es igual a 104m^2.
Sea “x” el ancho y “x+5”, el largo. Entonces, el área es igual a “x(x+5)”, que es igual a 104.
Esta es la ecuación algebraica que representa la situación.
La segunda pregunta dice:

Para resolver este tipo de ecuaciones, primero igualas a cero la ecuación.
En este caso, significa restar en ambos lados de la igualdad 104.
Y queda: x^2+5x-104 es igual a 104-104
Queda: x^2 +5x-104 es igual a 0
Esta ecuación se resuelve buscando el término común a dos binomios, que es “x”, y para formar los dos binomios se deben encontrar dos números que multiplicados den “-104”, y que sumados den 5.

Los números que multiplicados dan 104 son 2 y 52, 4 y 26, 8 y 13.
De éstos, se tiene que 52-2 es igual a 50, 26-4 es igual a 22 y 13 – 8 es igual a 5.
Ya tienes los dos números de los binomios: 13 y (-8), que multiplicados dan “-104”.
Así: ð‘¥^2+5ð‘¥−104=(ð‘¥+13)(ð‘¥−8)

De los dos binomios, se tiene que:
(ð‘¥+13)(ð‘¥−8) es igual a 0
Esto implica que alguno de los binomios o los dos son iguales a cero.
Si x+13 es igual a 0, entonces “x” es igual a -13.
Si x-8 es igual a 0, entonces “x” es igual a 8.
Y tienes dos soluciones para “x”: -13 y 8.
Responde la tercera pregunta: ¿cuánto debe medir el ancho y largo del corral?

Ya tienes que de (ð‘¥+13) (ð‘¥−8) = 0, hay dos soluciones y eliges la positiva, que es 8.
Se designó a “x” como el ancho, entonces, de ancho tiene 8 metros. El largo es “x+5”, así que 8+5 es igual a 13.
Las medidas son 8 m de ancho, 13 m de largo.
Has podido ayudar a Janet a resolver su problema.
Situación 2
- Audiovisual 2 “El poema cuadrático”

Has encontrado la situación del poema como una ecuación.
La segunda pregunta dice:

Se tiene que:
8(ð‘¥−1)(ð‘¥+1) = ð‘¥−8
Ahora, (ð‘¥−1)(ð‘¥+1) son binomios conjugados, lo que lleva a una diferencia de cuadrados.
Así, (ð‘¥−1)(ð‘¥+1) es igual a x^2-1^2, lo que hace que la ecuación w3q
8(ð‘¥^2−1^2) es igual a ð‘¥−8
8(ð‘¥^2−1) es igual a ð‘¥−8
Y ð‘¥^2−8 es igual a ð‘¥−8
Se resta 8 de ambos lados de la igualdad y queda: 8ð‘¥^2 es igual a ð‘¥
Ahora se divide entre x ambos lados del signo igual, (8ð‘¥^2)/ð‘¥ es igual a ð‘¥/ð‘¥. Como x^2 es igual a “x por x”, 8ð‘¥ð‘¥/ð‘¥ es igual a ð‘¥/ð‘¥, y una cantidad dividida entre sí misma es igual a uno, en este caso x/x es igual a uno.
Así: 8ð‘¥(uno) es igual a uno. Se divide entre 8 ambos lados de la igualdad. Queda:
8ð‘¥/8 es igual a 1/8
Por lo tanto, x es igual a 1/8.
Ya se tiene el valor de “x”.
La tercera pregunta dice:

Comprueba que es 1/8.
En las dos ecuaciones que obtuviste del poema, se sustituirá el valor encontrado, 1/8.
En 8(ð‘¥−1)(ð‘¥+1) y en x-8 se sustituirá “x” por 1/8.
Al sustituir 1/8 en 8(ð‘¥−1)(ð‘¥+1), se tiene: (1/8−1)(1/8+1) es igual a 8(1/8−8/8)(1/8+8/8)
Esto es igual a:
8 por (1−8)/8)(1+8)/8) es igual a = 8 por (−7)/8)(9/8), que es igual a 8 por(−7)(9))/(8)(8)
Al multiplicar (-7)(9) es igual a -63, y se multiplica una vez por 8 y se divide dos veces entre 8, así que es igual a -63/8.
Al sustituir 1/8 en x-8, se tiene que 1/8−64/8, ya que 64/8 es igual a 8.
1/8−64/8 es igual a (1-64)/8, es igual a -63/8
Por las dos expresiones generadas por el poema, se ha visto que “x” es igual a 1/8.
Situación 3
Como tercera situación, una alumna expone su problema, observa en qué le puedes ayudar.

La primera pregunta es:

Es un problema de área de un cuadrado en el que se conoce el área resultante: 484 metros cuadrados, y la medida del lado, (x+5).
El área del cuadrado es (x+5)^2, es igual a 484.
Desarrollando el cuadrado queda:
ð‘¥^2+10ð‘¥+25=484
Esta expresión algebraica representa al problema.
La segunda pregunta dice:

Para contestar esta pregunta, debes conocer el valor de “x”. Para esto, se ocupará la ecuación:
(ð‘¥ + 5)^2 es igual a 484
Para despejar “x”, hay que obtener la raíz cuadrada de cada lado de la igualdad.
La raíz cuadrada de (x+5)^2 es igual a x+5; la raíz cuadrada de 484 es 22.
Queda:
x+5 es igual a 22
Se resta 5 a cada lado de signo igual.
X+5-5 es igual a 22-5
Así, x es igual a 17
Ahora que tienes el valor de “x”, se puede obtener el área original, que es “x” al cuadrado, que es 17 al cuadrado, que es igual a 289 metros cuadrados.
La tercera pegunta es:

Ya se obtuvo el valor cuando se calculó la raíz cuadrada de 484. Resultado: 22 metros por lado.
Otra forma es ocupando el valor encontrado original, “x”, al que se le agregan 5 metros por lado, y queda igual la cantidad de 22 metros por lado.
Situación 4
- Audiovisual “El maíz”

La primera pregunta es:

Es un terreno cuadrado, donde se conoce el área total.
El lado “x” al cuadrado es igual a 1 225.
Entonces, la ecuación cuadrática que responde a esta pregunta es:
x^2 es igual a 1 225
La segunda pregunta dice:

Si se tiene que x^2 es igual a 1 225, entonces se aplica la raíz cuadrada a ambos lados de la igualdad.
Queda: raíz cuadrada de x^2 es igual a la raíz cuadrada de 1 225.
Así, x es igual a 35.
La tercera pregunta es:

Si se tienen 35 metros por lado y se debe sembrar cada planta de maíz cada 2 metros, entonces, por lado, se siembra 35 entre 2, que es igual a 17.
En total, se pueden sembrar (17)(17) igual a 289 plantas de maíz.
Realiza dos preguntas con respecto a las situaciones consideradas.
Selecciona y escribe a qué situación corresponde cada una de las representaciones geométricas.

La situación 1 se puede representar por el rectángulo de ancho “x” y largo “x+5”. Y a su lado se escribe: “Situación 1”.
La situación 2, el poema, no tiene representación aquí, así que no se escribe.
La situación 3 está representada por la primera figura, el cuadrado con lados x+5. Se escribe: “Situación 3”.
La situación 4 está representada por la segunda figura geométrica, el cuadrado de lado “x”. Se escribe: “Situación 4”.
Ahora resuelve la siguiente pregunta.
Relaciona las columnas correspondientes anotando en el paréntesis que corresponda a la ecuación correcta y su situación 1, 2, 3 o 4.

La primera situación, la del corral, en donde el largo mide 5 metros más que el ancho y su área es de 104 metros cuadrados, corresponde a x(x+5) es igual a 104. Se escribe: “Situación 1”.
La segunda situación, el del poema, donde se multiplican 8 veces el sucesor con el antecesor y es igual a la cantidad desconocida menos 6, corresponde a 8((ð‘¥+1)(ð‘¥−1)) igual a ð‘¥−8x(x+5). Se escribe: “Situación 2”.
La tercera situación, la de la plaza cívica, donde se aumentó en 5 metros por lado a la plaza original cuadrada, conociendo que el área final es de 484 metros cuadrados, corresponde a (ð‘¥+5)(ð‘¥+5) es igual a 484. Se escribe: “Situación 3”.
La cuarta situación, en donde se busca lo que mide el lado de un terreno cuadrado de área igual a 1 225 metros cuadrados, corresponde a ð‘¥^2=1225.
En esta sesión aprendiste la solución de problemas reales aplicando las ecuaciones de segundo grado y resolviéndolas con diferentes procesos de solución.
No hay comentarios.:
Publicar un comentario