MATEMÁTICAS - SECUNDARIA 2
Unidades de capacidad en el Sistema Internacional de Medidas y el Sistema Inglés
(MIÉRCOLES 03 MARZO)
ACTIVIDAD:
Consulta tu libro de texto de Matemáticas y resuelve algunos de los problemas o ejercicios que impliquen conversiones de unidades de “capacidad” en el Sistema Internacional de Medidas y en el Sistema Inglés.
RESUMEN:
Para iniciar es importante recordar que, en México se tienen como medidas oficiales las descritas por el Sistema Internacional de Unidades, esto se plasma en la Norma Oficial Mexicana NOM-008-SCFI-2002, denominada Sistema General de Unidades de Medida.
Como punto de partida, reflexiona en los siguiente:
¿Qué es la capacidad?
Capacidad, es la propiedad de algunos objetos de contener sustancias en su interior, su unidad de medida en el Sistema Internacional es el metro cúbico, un metro cúbico es un cubo que mide un metro en sus aristas. También es posible medirlo en centímetros cúbicos, decímetros cúbicos y en los diferentes múltiplos y submúltiplos del metro cúbico, aunque usualmente se utiliza el litro y el mililitro.
Por ejemplo, un metro cúbico equivale a mil litros. El mililitro es un submúltiplo del litro y es la milésima parte de un litro, por lo tanto, un litro equivale a mil mililitros.
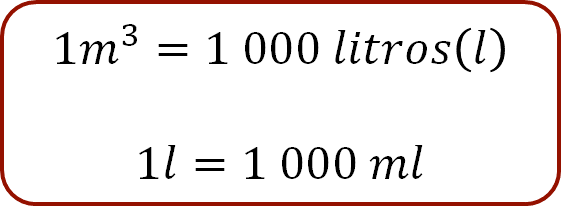
En el Sistema Inglés también existen medidas de capacidad. Las más usuales son el galón, la onza de fluido, la taza y también se pueden encontrar el pie cúbico y la pulgada cúbica.
Estas medidas tienen una equivalencia en el Sistema Internacional. El galón equivale a 3.785 litros, una onza de fluido a 29.5735 mililitros y una taza equivale a 240 mililitros.
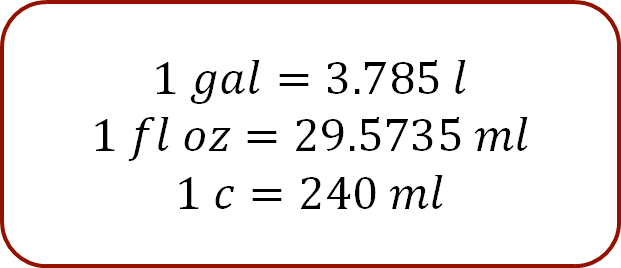
Para el caso de los pies y las pulgadas cubicas, se realiza la conversión tomando en cuenta la equivalencia en metros elevada al cubo.
Es importante tener presente estas equivalencias, ya que son la base para poder convertir unidades de capacidad entre el Sistema Internacional de Unidades y el Sistema Inglés. Para observar su aplicación, trabajarás con algunas situaciones problemáticas.
Problema 1: auto, galones-litros
Mariel ha comprado un auto estadounidense. El manual del usuario indica que la capacidad del tanque de combustible es de 15 galones.
¿Con cuántos litros podrá llenar Mariel el tanque del auto?
Para responder la pregunta, se debe tener en cuenta la equivalencia entre galones y litros. Un galón equivale a 3.785 litros.
Para encontrar la capacidad en litros del tanque del auto de Mariel, se plantea una igualdad en la que se incluye la equivalencia antes mencionada entre galón y litros, para establecer una ecuación que permita realizar la conversión. De manera general, para realizar la conversión de unidades, se plantea la siguiente ecuación: Unidades a obtener es igual a unidades actuales por factor de conversión.
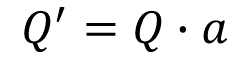
Donde:
Q´ = unidades a obtener.
Q = unidades actuales
a = factor de conversión.
En el problema planteado se tiene la siguiente expresión:
Capacidad en litros igual a 15 galones por el factor de conversión 3.785 sobre un galón.
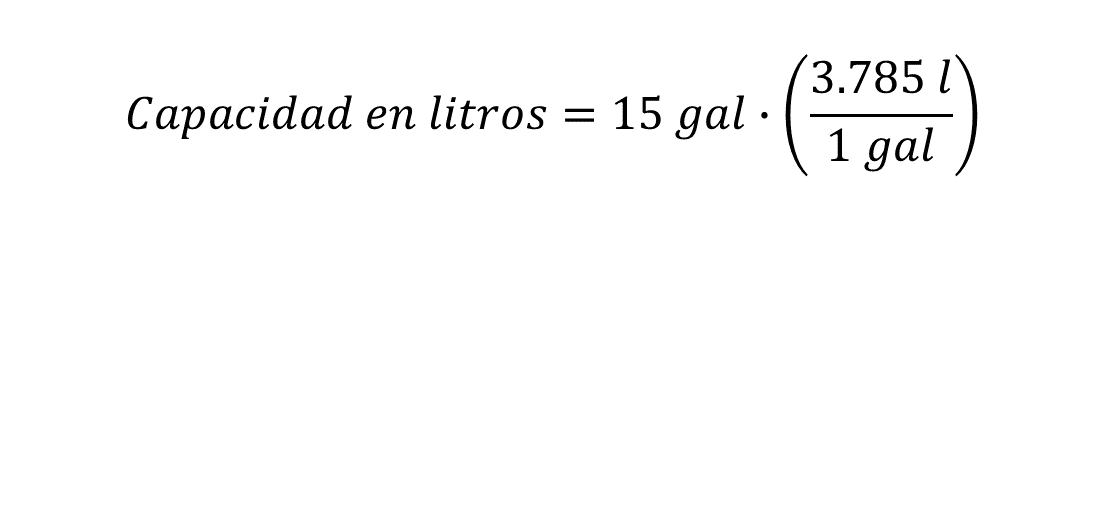
De esta manera, se indican las siguientes operaciones:
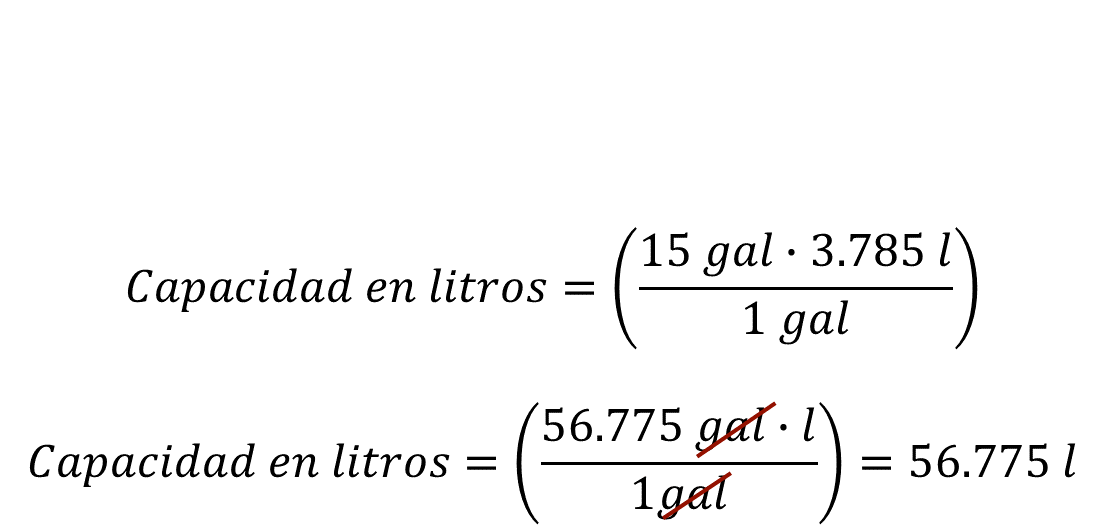
Al realizar los cálculos resulta 56.775 litros. Por lo tanto, Mariel debe comprar 56.775 litros para llenar el tanque de su automóvil.
Continúa con otro problema.
Problema 2: alberca, metros cúbicos-galones
Adrián tiene una alberca con una capacidad de 9.47 metros cúbicos. La persona de mantenimiento le indicó que debe colocar una pastilla de cloro por cada cien galones de agua.
¿Cuántas pastillas debe colocar si la alberca se encuentra totalmente llena?
Para responder la interrogante se debe obtener primero la capacidad de la alberca en galones. Para ello, se plantea la ecuación general con el respectivo factor de conversión. En este caso, un metro cúbico es igual a mil litros y 3.785 litros equivalen a un galón.
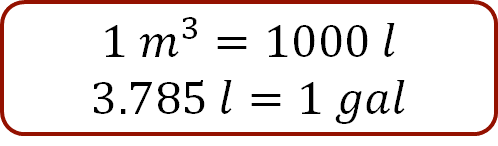
Para indicar la equivalencia entre metros cúbicos y litros, se plantea la expresión: capacidad en litros igual a 9.47 metros cúbicos, multiplicada por el factor de conversión mil litros sobre un metro cúbico.
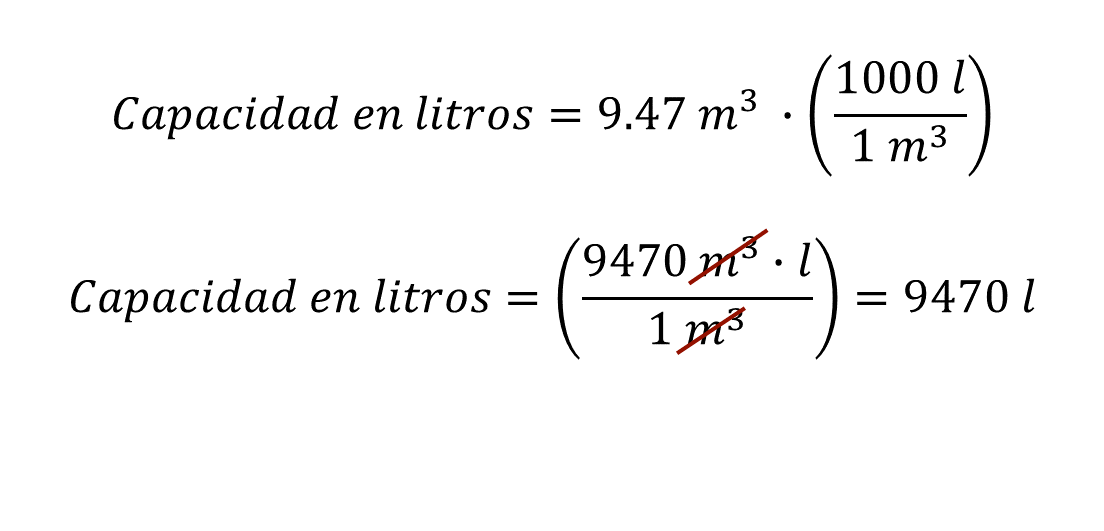
Al realizar las operaciones, el resultado es 9470 litros, ya que el metro cúbico se reduce.
Después, se calcula la capacidad en galones con la igualdad 9470 litros por un galón sobre 3.785 litros:
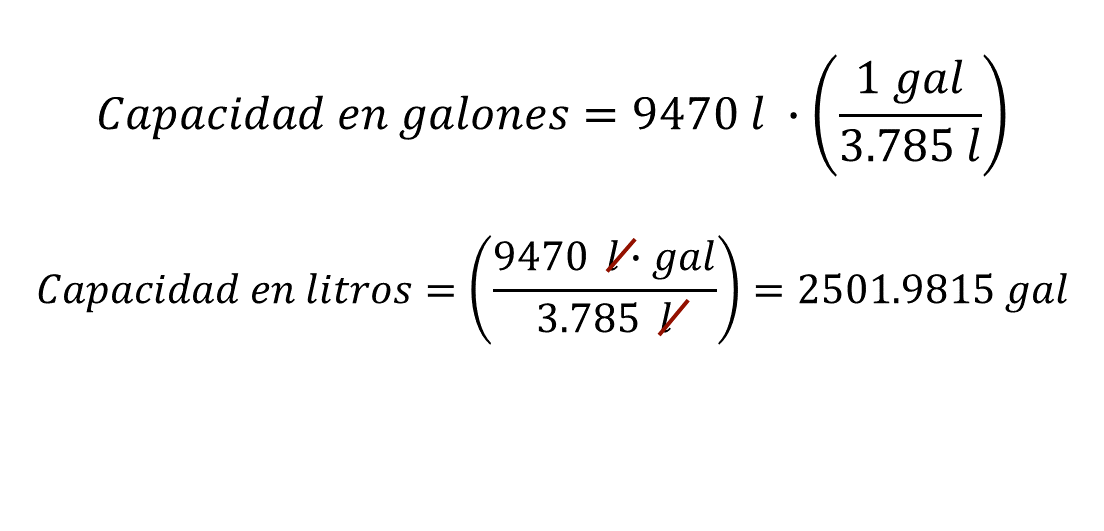
Al calcular el cociente, el resultado es 2501.9815 galones, ya que los litros se reducen.
Una vez calculada la capacidad de la alberca en galones existen las condiciones para saber la cantidad de pastillas que Adrián debe colocar en su alberca.
Según las indicaciones de la persona de mantenimiento, por cada cien galones se debe colocar una pastilla de cloro. En este caso, la capacidad en galones puede aproximarse a los 2500 galones, al dividir esta cantidad entre cien, el cociente será el número de pastillas de cloro que deben ponerse en la alberca.
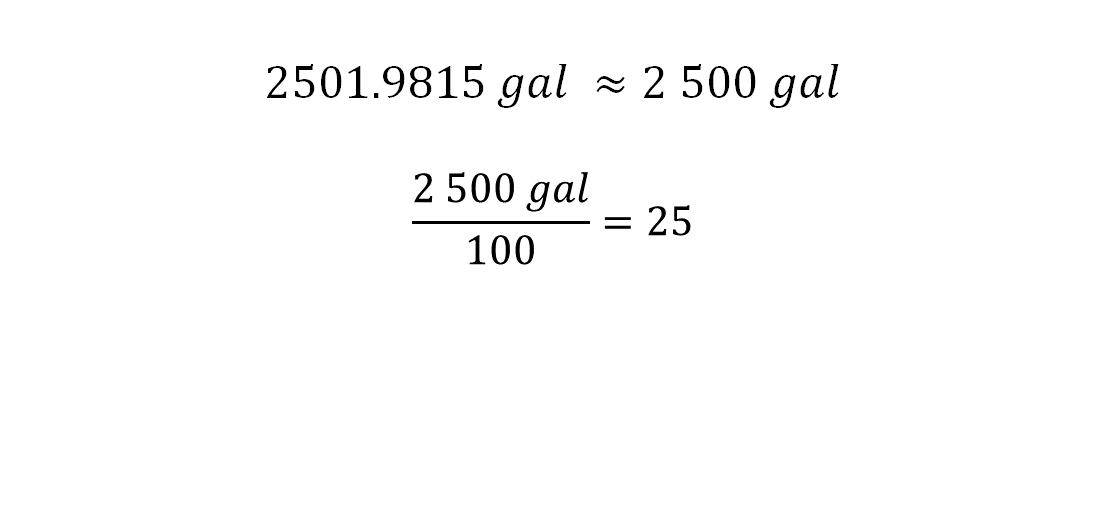
Adrián debe colocar 25 pastillas de cloro, cuando ésta se encuentre totalmente llena.
Como puedes observar, la conversión de unidades se realiza mediante la aplicación sucesiva de factores de conversión, en este caso, se realizaron uno a la vez, pero es posible plantearlos desde la primera expresión, lo cual se indica de la siguiente manera:
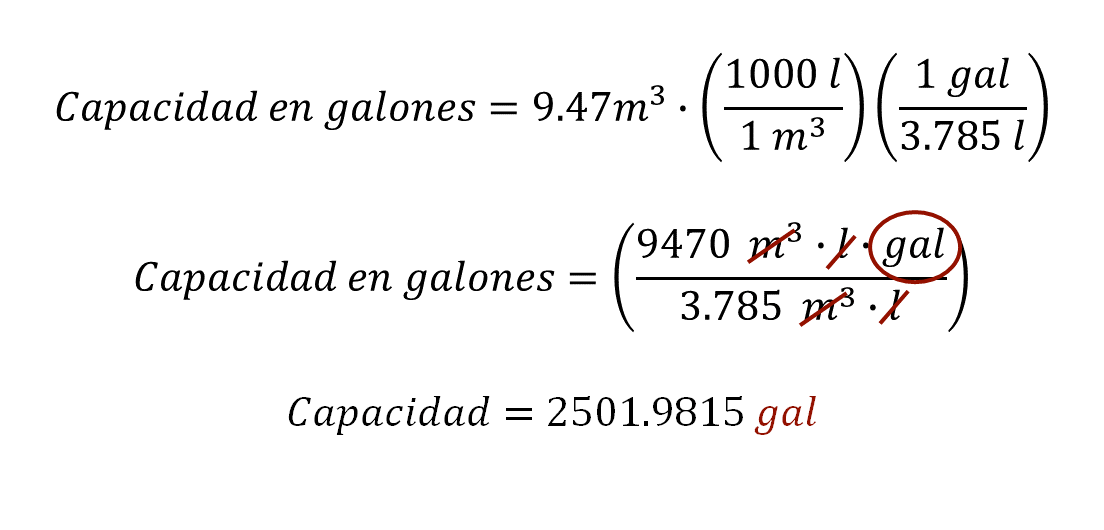
En este caso son, 2501.9815 galones. Que es el mismo resultado obtenido con el procedimiento anterior.
El trabajo realizado con las unidades de medida es lo que se denomina análisis dimensional, y resulta sumamente útil para realizar de manera correcta las conversiones de unidades.
Analiza otro problema.
Problema 3: pastel, tazas/onzas-mililitros
Frida quiere hacer un pastel, el empaque de la harina indica que debe agregar dos tazas de agua (c) y ocho onzas de fluido (fl oz) de aceite, además de seis huevos.
¿Cuántos mililitros de agua y cuántos mililitros de aceite debe agregar para obtener la masa adecuada?
Para saber la cantidad de agua y aceite necesarios, se debe realizar la conversión de unidades a mililitros.
En el primer caso, se estable la relación: capacidad en mililitros igual a 2 tazas por el factor de conversión 240 mililitros sobre una taza.

Lo que da como resultado 480 mililitros, una vez realizado el análisis dimensional y reducidas la medida tazas del numerador y del denominador.
Para determinar la cantidad de aceite en mililitros que debe agregar Frida a la masa, se establece la relación: capacidad en mililitros igual a 8 onzas de fluido por el factor de conversión 29.5735 mililitros sobre una onza de fluido.
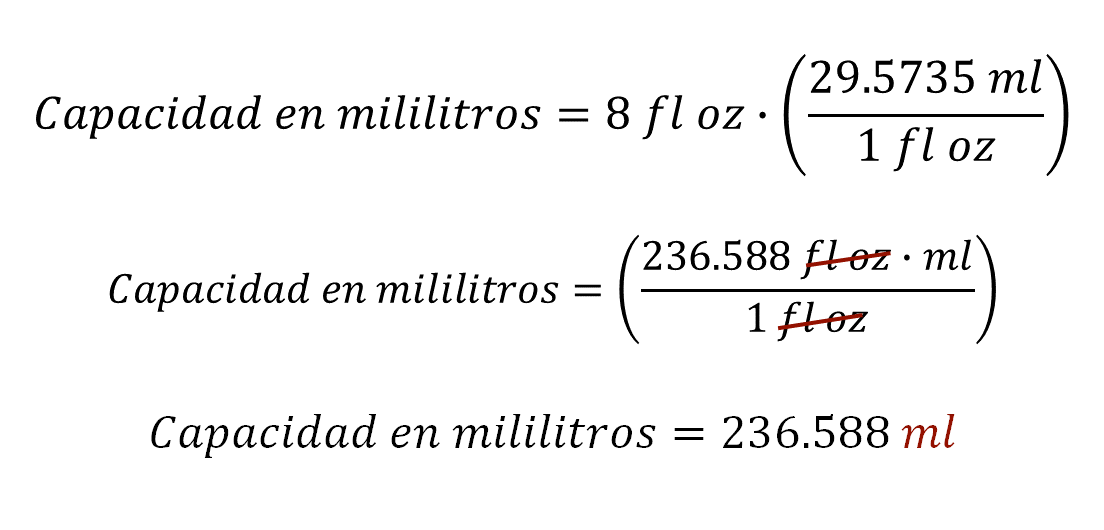
Al resolver las operaciones, el resultado es el producto 236.588 mililitros, ya que las onzas de fluido se reducen.
La cantidad de agua y de aceite que debe agregar Frida a la harina para realizar el pastel es 480 mililitros de agua y aproximadamente 237 mililitros de aceite, además de los seis huevos.
Comparen estos resultados con las estimaciones que realizaste al iniciar la resolución de este problema.
Resuelve otro problema que implica una nueva conversión.
Problema 4: tinacos, litros-pies cúbicos.
La capacidad usual de los tinacos de casa habitación es de 1100 litros, ¿cuál es la capacidad en pies cúbicos?
Para resolver este problema, se establece un factor de conversión entre los litros y los metros cúbicos, posteriormente otra conversión para los metros y pies cúbicos.
Para pasar de litros a pies cúbicos, se multiplica la capacidad expresada en litros por el factor de conversión un metro cúbico sobre mil litros, y por el factor de conversión 35.315 pies cúbicos sobre un metro cúbico.
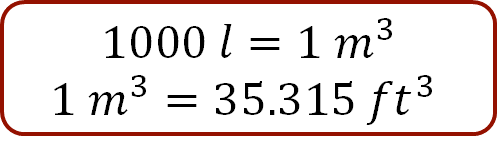
Ten presente que la conversión de unidades puede realizarse multiplicando sucesivamente la cantidad a convertir, en este caso, los mil cien litros por los factores de conversión necesarios para lograr las unidades deseadas, los pies cúbicos.
De esta manera la expresión a resolver es:
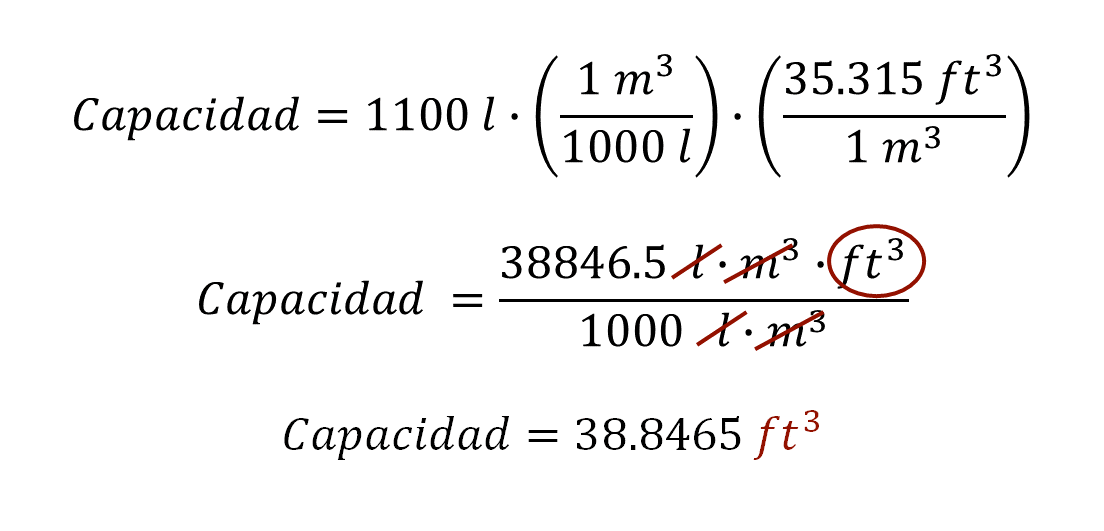
Entonces, la capacidad del tinaco, expresada en pies cúbicos, es equivalente a 38.8465 pies cúbicos.
Continúa poniendo en práctica los factores de conversión, resolviendo el siguiente problema.
Problema 5: cámara fría, metros cúbicos-pies cúbicos
Mary es dueña de una empresa de refrigeración. Por expansión debe instalar una cámara fría de 71 metros cúbicos. Al cotizarla le indican que el precio de instalación es de $110 por pie cúbico, ¿cuál será el costo aproximado de dicha instalación?
Para dar solución al problema, analiza los datos para poder plantear el factor o factores de conversión. En este caso, observa que hay que convertir la capacidad mostrada de metros cúbicos a pies cúbicos.
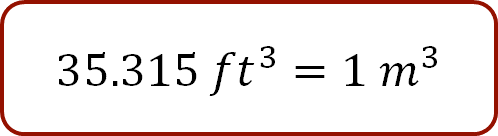
Posteriormente, se calcula el costo aproximado teniendo presente la referencia dada en la cotización, cada pie cúbico cuesta ciento diez pesos. ¿Cuánto estimas que será el costo de instalación de esa cámara fría?

Teniendo en cuenta la equivalencia entre pies y metros cúbicos, se establece la ecuación con el respectivo factor de conversión. De tal manera, queda planteada la siguiente relación.
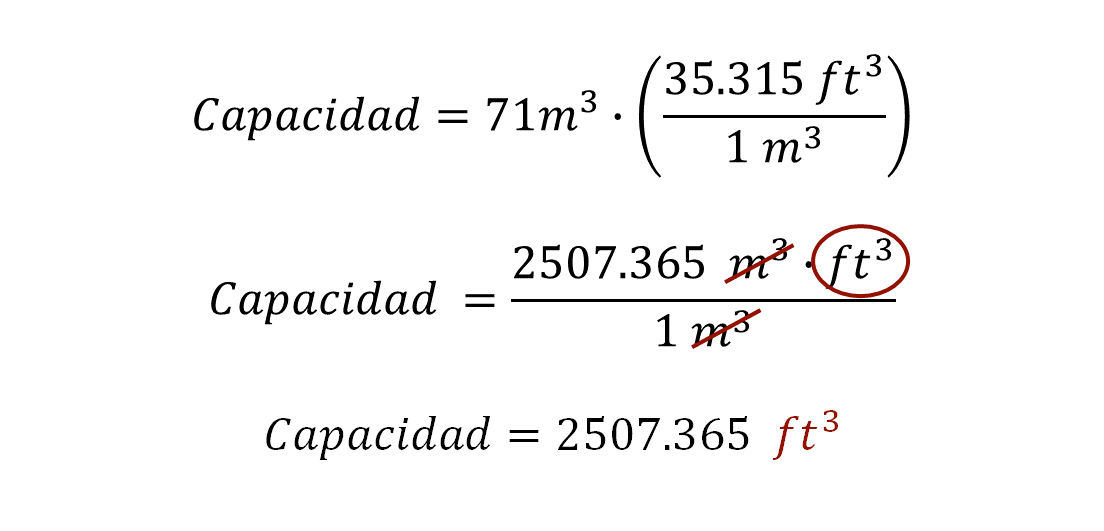
Por lo tanto, se obtienen 2507.365, el resultado se expresará en pies cúbicos. Se puede afirmar que la capacidad de la cámara de refrigeración que va a instalar Mary es de 2507.365 pies cúbicos.
Con esta información, ya se puede calcular el costo aproximado de la instalación.
El costo de instalación por pie cúbico es de ciento diez pesos; por lo tanto, para saber el costo de la instalación de la cámara de refrigeración bastará con multiplicar el costo proporcionado en la cotización, por la capacidad calculada anteriormente, es decir:
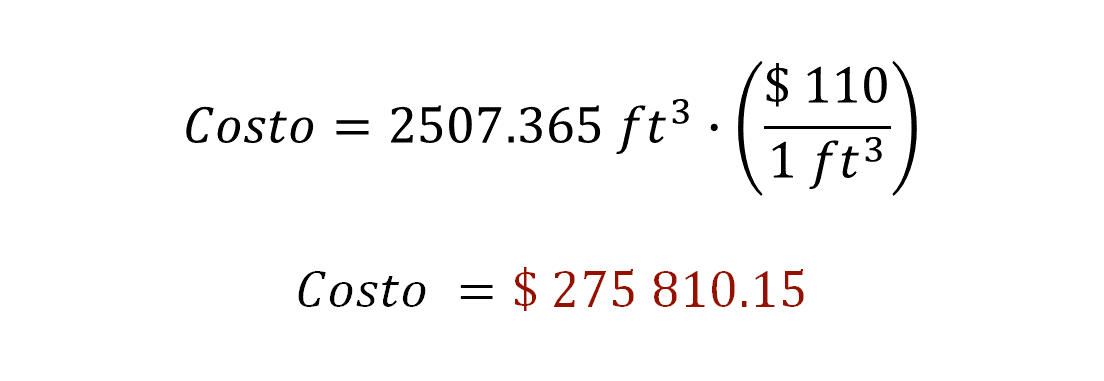
El resultado es 275,810.15 pesos, como costo de instalación de la cámara fría. Es posible aproximar este costo a 276,000 pesos, que es lo que Mary debe invertir para lograr instalar la cámara fría.
Como puedes notar, la clave para realizar conversiones de unidades está en conocer las equivalencias entre ellas, pues de esta manera es posible establecer los factores de conversión, y también se puede multiplicar por los factores de conversión necesarios con el fin de obtener las unidades de capacidad deseadas.
A continuación, se muestra una tabla con las medidas de capacidad y sus equivalencias utilizadas hasta el momento.
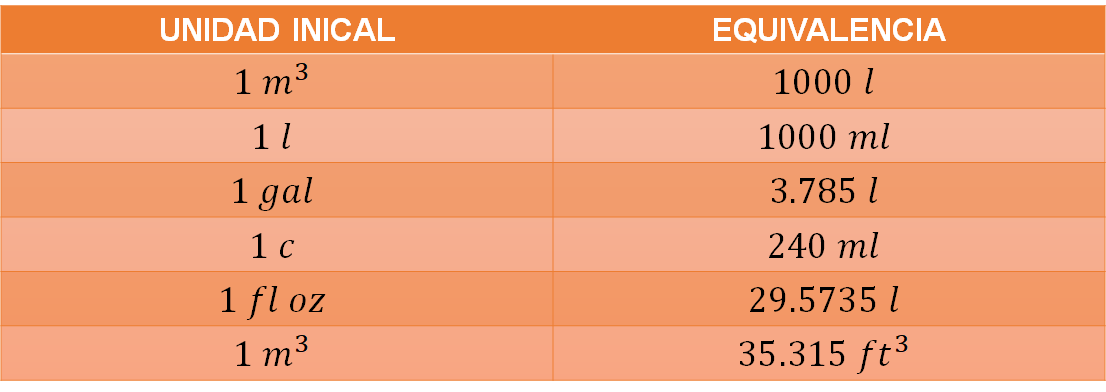
Un metro cúbico equivale a mil litros, un litro equivale a mil mililitros, un galón corresponde a 3.785 litros, una taza es equivalente a 240 mililitros, una onza de fluido es igual a 29.5735 mililitros y un metro cúbico es equivalente a 35.315 pies cúbicos.
De manera individual, o con ayuda de tu profesora o profesor de grupo, puedes plantear los factores de conversión que desees, por ejemplo, de metros cúbicos a galones, de onzas de fluido a metros cúbicos o los que te imagines en cuanto a unidades de capacidad se refiere, sólo debes tomar en cuenta la equivalencia entre unidades.
Utilizando las equivalencias anteriores, realicen los siguientes ejercicios.
Ejercicio 1: convierte 20 litros a tazas, para lograrlo, considera las equivalencias necesarias, en este caso, un litro es igual a mil mililitros y una taza es igual a 240 mililitros.
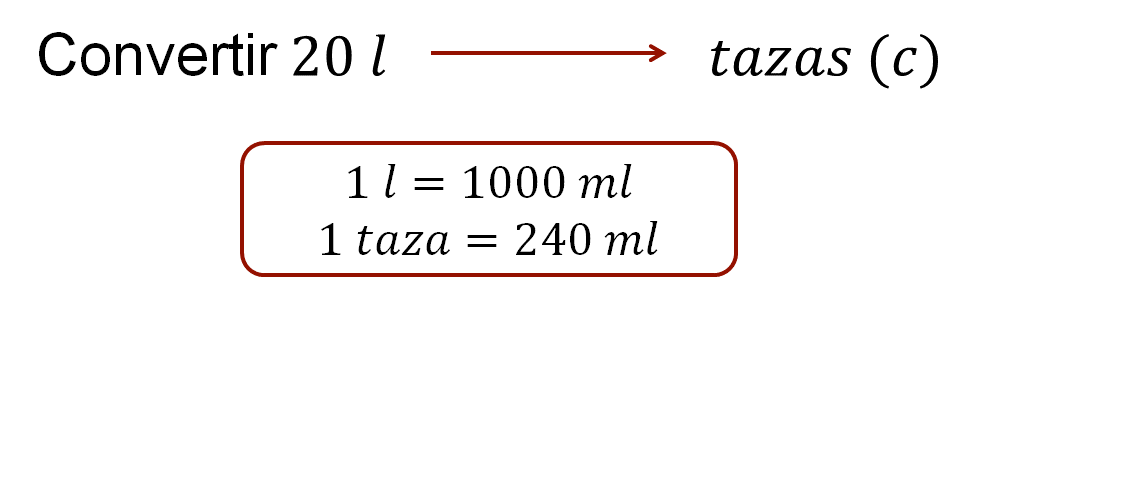
Antes de iniciar la resolución contesta en tu cuaderno las siguientes preguntas: ¿cuántos factores de conversión se deben aplicar para lograr esta conversión?, ¿cuál o cuáles son esos factores de conversión?
Son dos los factores de conversión que se deben aplicar en este problema.
Multiplica 20 litros por el factor mil mililitros sobre un litro y también por el factor una taza sobre 240 mililitros.
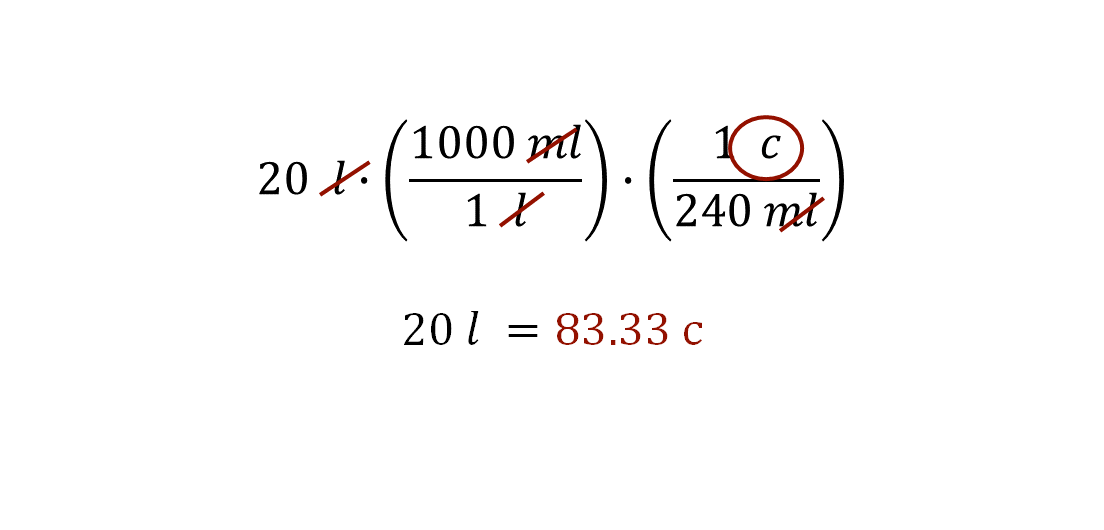
El resultado numérico de las operaciones es 83.33 tazas.
Ejercicio 2: convierte 6 galones a mililitros. Considera las equivalencias, un galón es igual 3.785 litros y un litro es igual a mil mililitros.
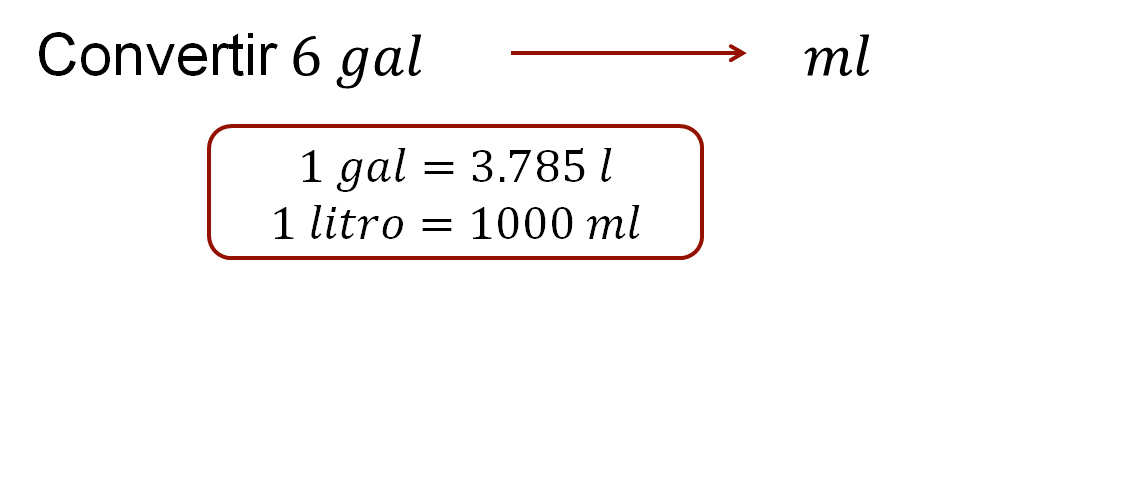
Con base en lo realizado hasta el momento, contesta: ¿cuántos factores de conversión se deben aplicar para determinar cuántos mililitros son equivalentes a seis galones? Realiza una estimación del número de mililitros que son equivalentes a seis galones y anótalo en tu cuaderno.
Al establecer la relación para esta conversión se utilizan los dos factores de conversión mencionados antes. Quedando de la siguiente manera:
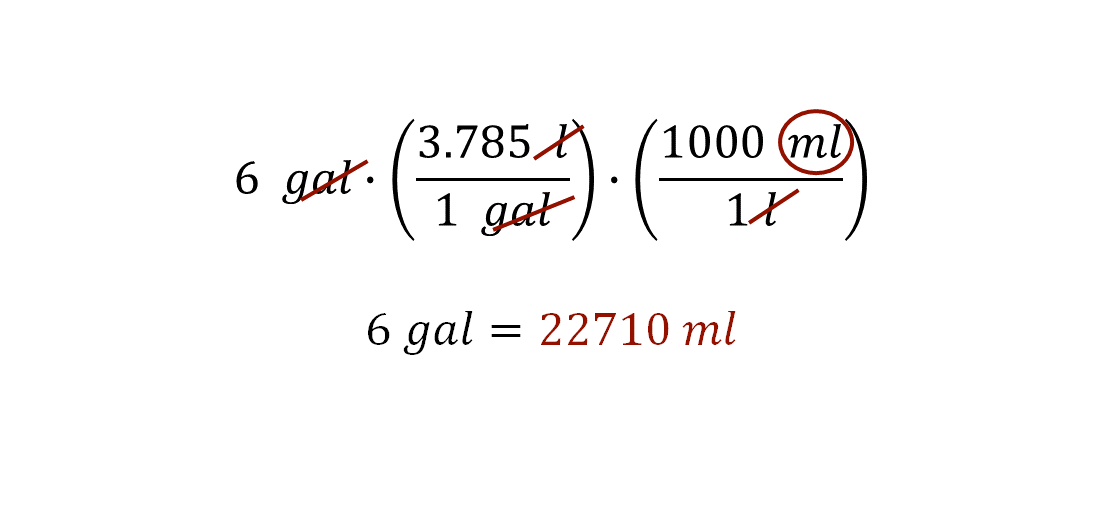
El resultado indica que seis galones equivalen a 22,710 mililitros. Compara este resultado con la estimación que hiciste antes de resolver este ejercicio.
Ejercicio 3: convierte treinta y cuatro onzas de fluido a litros. Considera las equivalencias, una onza de fluido equivale a 29.5735 mililitros y un litro es igual a mil mililitros.

Estima el resultado y contesta en tu cuaderno: ¿resultarán más de treinta cuatro litros o menos de treinta y cuatro litros?, ¿por qué?
Establece la relación para convertir, 34 onzas de fluido por el factor 29.5735 mililitros sobre una onza de fluido y también por el factor un litro sobre mil mililitros.
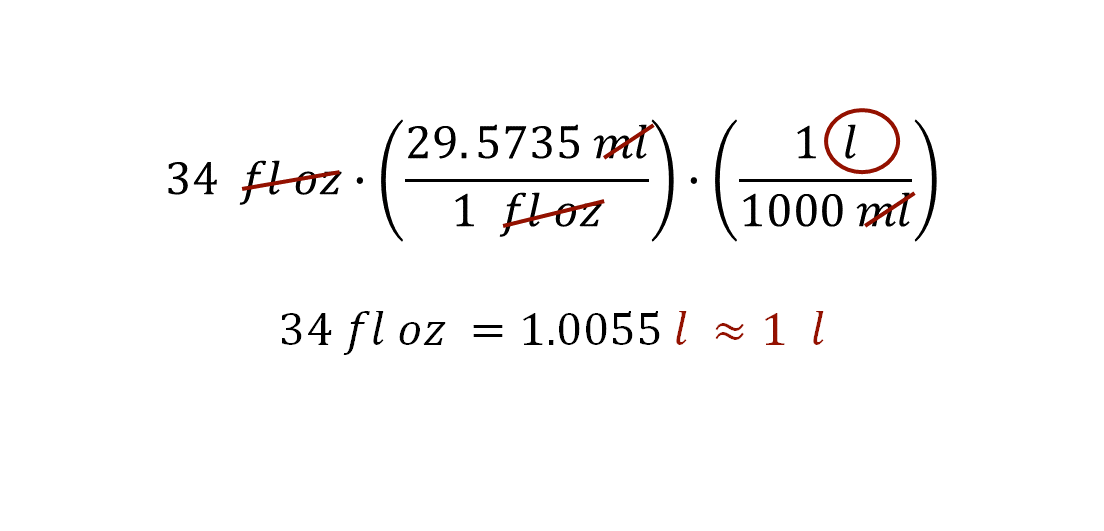
Al realizar las operaciones numéricas como la reducción de unidades, el resultado es 1.0055 litros. Es posible aproximar el resultado a un litro, es decir, 34 onzas de fluido equivalen aproximadamente a un litro.
Ejercicio 4: convierte noventa y seis mil tazas a metros cúbicos. Considera las siguientes equivalencias, una taza equivale a 240 mililitros, mil mililitros son iguales a un litro y, por último, mil litros equivalen a un metro cúbico.
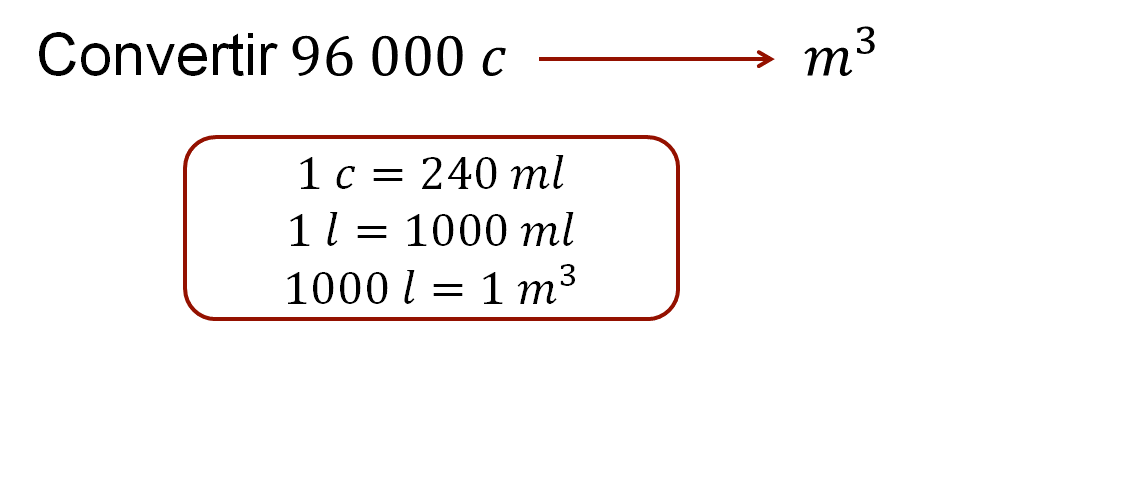
De acuerdo con estas equivalencias, ¿cuántos factores de conversión se deben aplicar para determinar la equivalencia en este ejercicio?, ¿cuántos metros cúbicos estimas que son equivalentes a noventa y seis mil tazas?
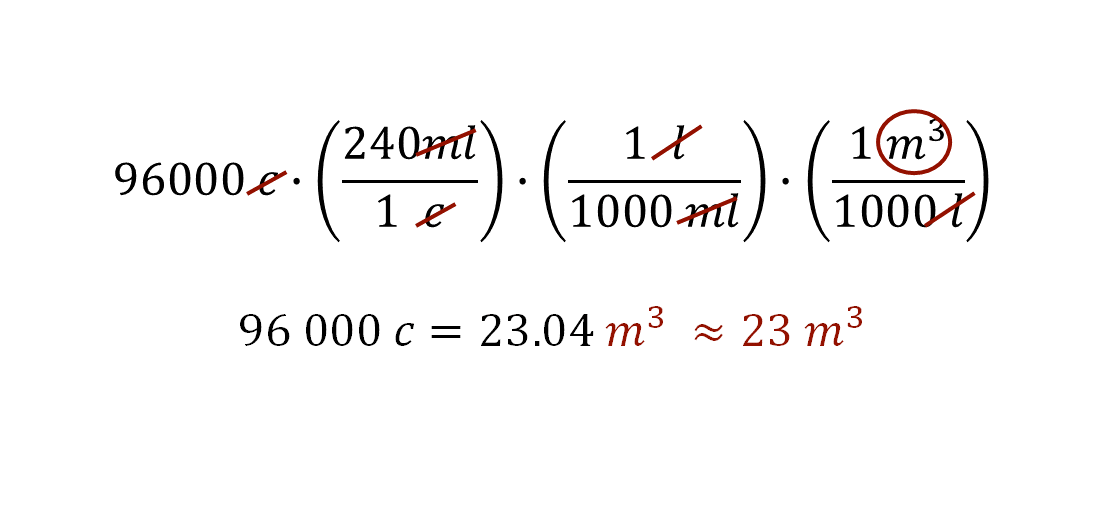
El resultado de la conversión de noventa y seis mil tazas es equivalente a 23.04 metros cúbicos, que se puede aproximar a 23 metros cúbicos.
En el caso de las conversiones, es primordial tener presentes las equivalencias entre unidades, para establecer los factores de conversión y lograr resolver correctamente los problemas que se presenten.
Con esto, has concluido la sesión. Recuera que éste es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí.
Para iniciar es importante recordar que, en México se tienen como medidas oficiales las descritas por el Sistema Internacional de Unidades, esto se plasma en la Norma Oficial Mexicana NOM-008-SCFI-2002, denominada Sistema General de Unidades de Medida.
Como punto de partida, reflexiona en los siguiente:
¿Qué es la capacidad?
Capacidad, es la propiedad de algunos objetos de contener sustancias en su interior, su unidad de medida en el Sistema Internacional es el metro cúbico, un metro cúbico es un cubo que mide un metro en sus aristas. También es posible medirlo en centímetros cúbicos, decímetros cúbicos y en los diferentes múltiplos y submúltiplos del metro cúbico, aunque usualmente se utiliza el litro y el mililitro.
Por ejemplo, un metro cúbico equivale a mil litros. El mililitro es un submúltiplo del litro y es la milésima parte de un litro, por lo tanto, un litro equivale a mil mililitros.
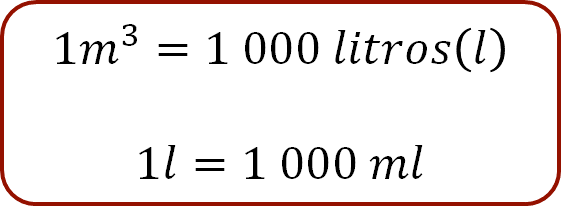
En el Sistema Inglés también existen medidas de capacidad. Las más usuales son el galón, la onza de fluido, la taza y también se pueden encontrar el pie cúbico y la pulgada cúbica.
Estas medidas tienen una equivalencia en el Sistema Internacional. El galón equivale a 3.785 litros, una onza de fluido a 29.5735 mililitros y una taza equivale a 240 mililitros.
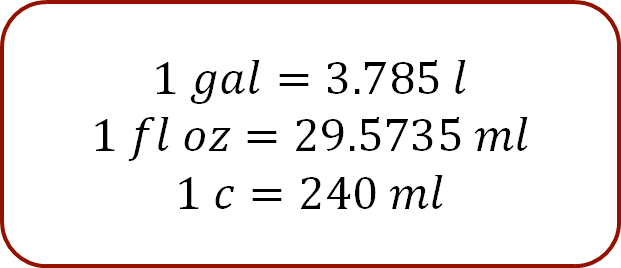
Para el caso de los pies y las pulgadas cubicas, se realiza la conversión tomando en cuenta la equivalencia en metros elevada al cubo.
Es importante tener presente estas equivalencias, ya que son la base para poder convertir unidades de capacidad entre el Sistema Internacional de Unidades y el Sistema Inglés. Para observar su aplicación, trabajarás con algunas situaciones problemáticas.
Problema 1: auto, galones-litros
Mariel ha comprado un auto estadounidense. El manual del usuario indica que la capacidad del tanque de combustible es de 15 galones.
¿Con cuántos litros podrá llenar Mariel el tanque del auto?
Para responder la pregunta, se debe tener en cuenta la equivalencia entre galones y litros. Un galón equivale a 3.785 litros.
Para encontrar la capacidad en litros del tanque del auto de Mariel, se plantea una igualdad en la que se incluye la equivalencia antes mencionada entre galón y litros, para establecer una ecuación que permita realizar la conversión. De manera general, para realizar la conversión de unidades, se plantea la siguiente ecuación: Unidades a obtener es igual a unidades actuales por factor de conversión.
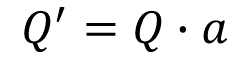
Donde:
Q´ = unidades a obtener.
Q = unidades actuales
a = factor de conversión.
En el problema planteado se tiene la siguiente expresión:
Capacidad en litros igual a 15 galones por el factor de conversión 3.785 sobre un galón.
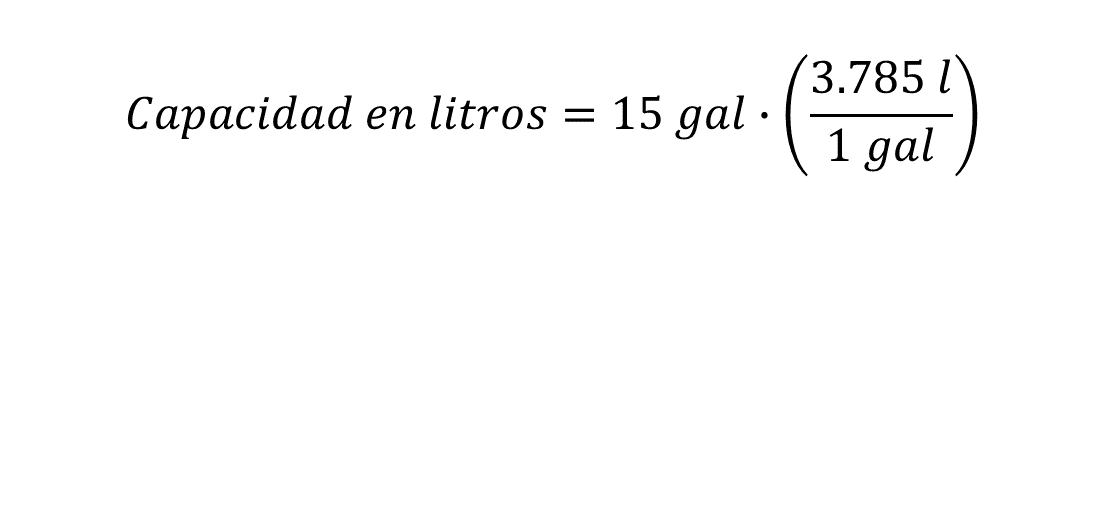
De esta manera, se indican las siguientes operaciones:
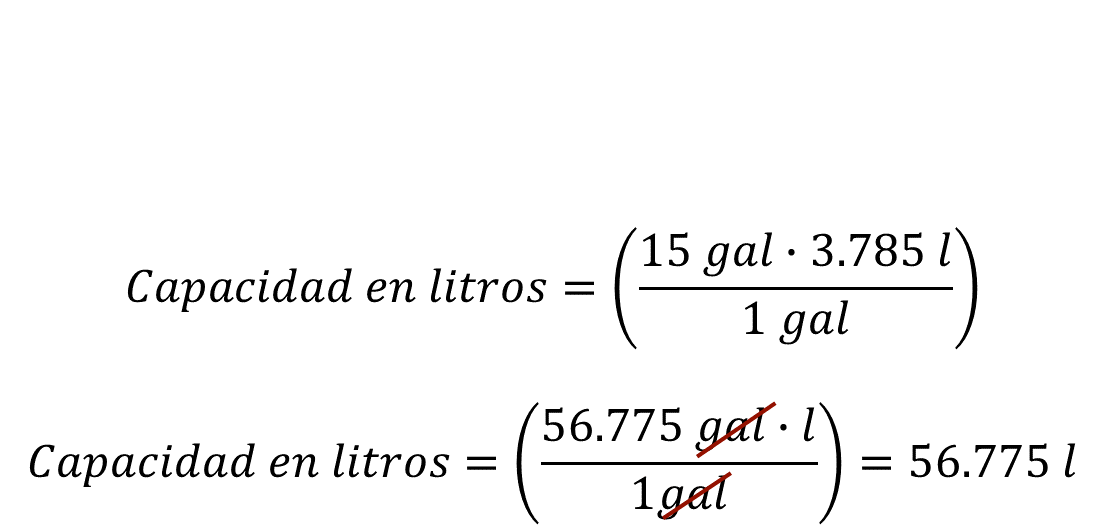
Al realizar los cálculos resulta 56.775 litros. Por lo tanto, Mariel debe comprar 56.775 litros para llenar el tanque de su automóvil.
Continúa con otro problema.
Problema 2: alberca, metros cúbicos-galones
Adrián tiene una alberca con una capacidad de 9.47 metros cúbicos. La persona de mantenimiento le indicó que debe colocar una pastilla de cloro por cada cien galones de agua.
¿Cuántas pastillas debe colocar si la alberca se encuentra totalmente llena?
Para responder la interrogante se debe obtener primero la capacidad de la alberca en galones. Para ello, se plantea la ecuación general con el respectivo factor de conversión. En este caso, un metro cúbico es igual a mil litros y 3.785 litros equivalen a un galón.
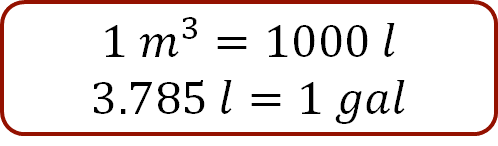
Para indicar la equivalencia entre metros cúbicos y litros, se plantea la expresión: capacidad en litros igual a 9.47 metros cúbicos, multiplicada por el factor de conversión mil litros sobre un metro cúbico.
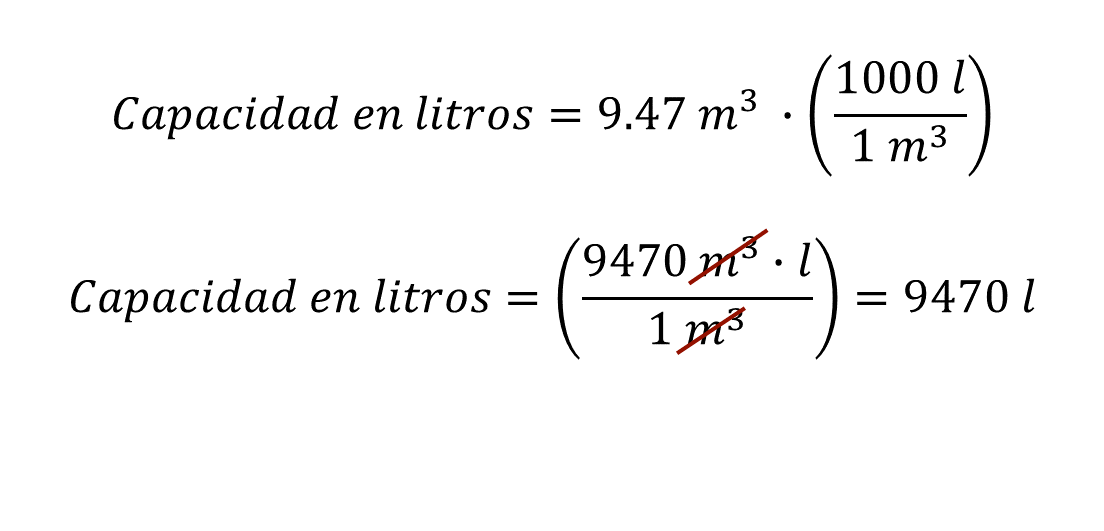
Al realizar las operaciones, el resultado es 9470 litros, ya que el metro cúbico se reduce.
Después, se calcula la capacidad en galones con la igualdad 9470 litros por un galón sobre 3.785 litros:
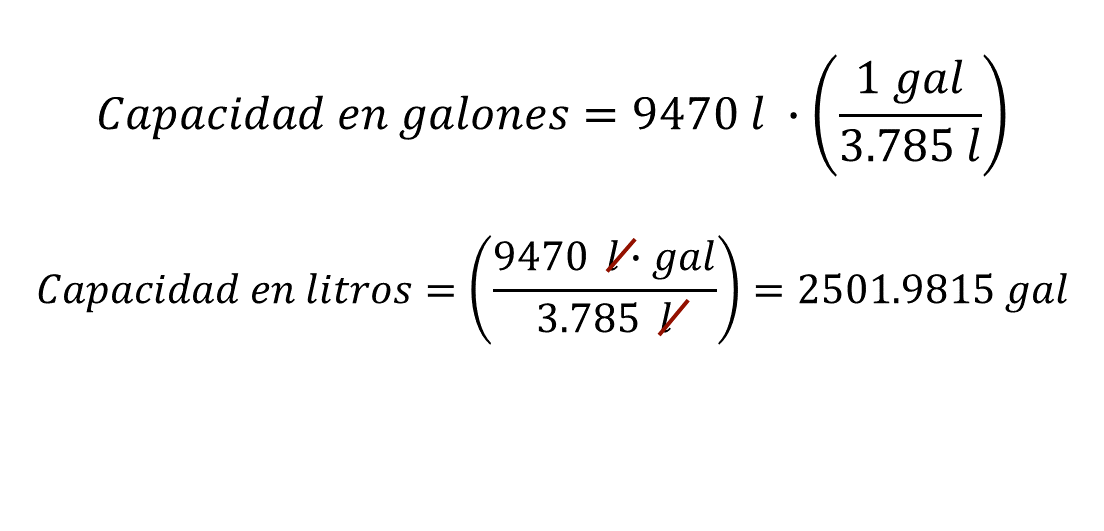
Al calcular el cociente, el resultado es 2501.9815 galones, ya que los litros se reducen.
Una vez calculada la capacidad de la alberca en galones existen las condiciones para saber la cantidad de pastillas que Adrián debe colocar en su alberca.
Según las indicaciones de la persona de mantenimiento, por cada cien galones se debe colocar una pastilla de cloro. En este caso, la capacidad en galones puede aproximarse a los 2500 galones, al dividir esta cantidad entre cien, el cociente será el número de pastillas de cloro que deben ponerse en la alberca.
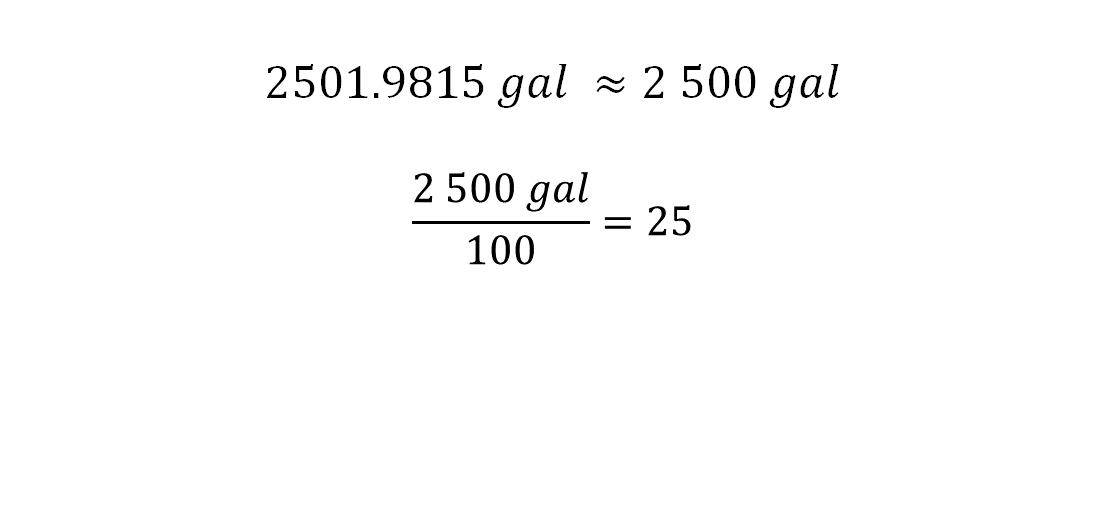
Adrián debe colocar 25 pastillas de cloro, cuando ésta se encuentre totalmente llena.
Como puedes observar, la conversión de unidades se realiza mediante la aplicación sucesiva de factores de conversión, en este caso, se realizaron uno a la vez, pero es posible plantearlos desde la primera expresión, lo cual se indica de la siguiente manera:
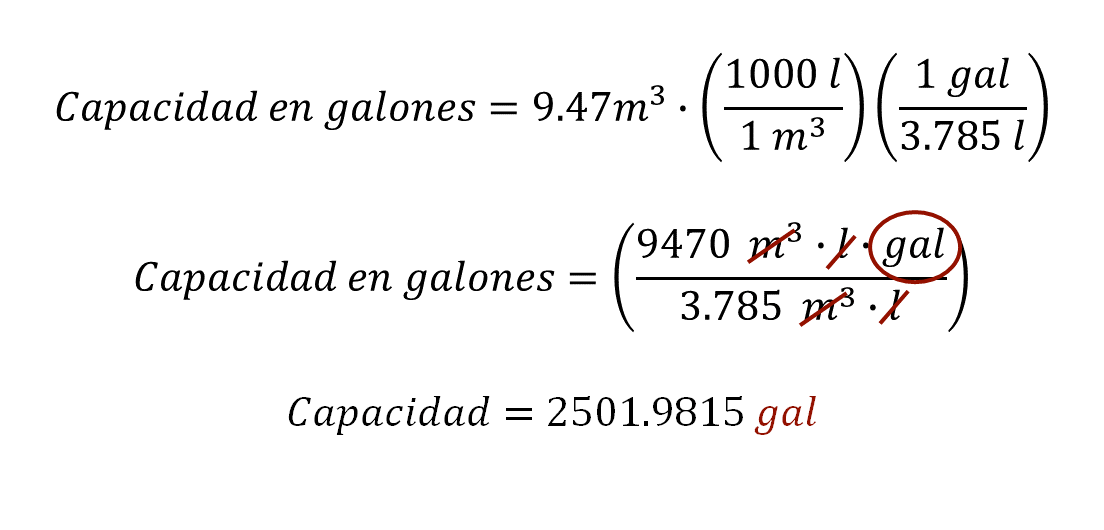
En este caso son, 2501.9815 galones. Que es el mismo resultado obtenido con el procedimiento anterior.
El trabajo realizado con las unidades de medida es lo que se denomina análisis dimensional, y resulta sumamente útil para realizar de manera correcta las conversiones de unidades.
Analiza otro problema.
Problema 3: pastel, tazas/onzas-mililitros
Frida quiere hacer un pastel, el empaque de la harina indica que debe agregar dos tazas de agua (c) y ocho onzas de fluido (fl oz) de aceite, además de seis huevos.
¿Cuántos mililitros de agua y cuántos mililitros de aceite debe agregar para obtener la masa adecuada?
Para saber la cantidad de agua y aceite necesarios, se debe realizar la conversión de unidades a mililitros.
En el primer caso, se estable la relación: capacidad en mililitros igual a 2 tazas por el factor de conversión 240 mililitros sobre una taza.

Lo que da como resultado 480 mililitros, una vez realizado el análisis dimensional y reducidas la medida tazas del numerador y del denominador.
Para determinar la cantidad de aceite en mililitros que debe agregar Frida a la masa, se establece la relación: capacidad en mililitros igual a 8 onzas de fluido por el factor de conversión 29.5735 mililitros sobre una onza de fluido.
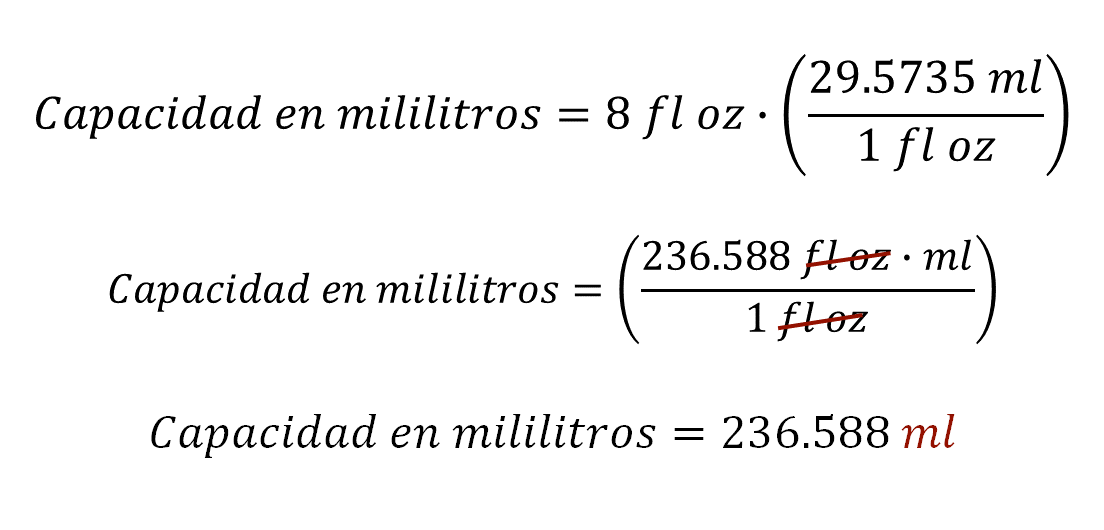
Al resolver las operaciones, el resultado es el producto 236.588 mililitros, ya que las onzas de fluido se reducen.
La cantidad de agua y de aceite que debe agregar Frida a la harina para realizar el pastel es 480 mililitros de agua y aproximadamente 237 mililitros de aceite, además de los seis huevos.
Comparen estos resultados con las estimaciones que realizaste al iniciar la resolución de este problema.
Resuelve otro problema que implica una nueva conversión.
Problema 4: tinacos, litros-pies cúbicos.
La capacidad usual de los tinacos de casa habitación es de 1100 litros, ¿cuál es la capacidad en pies cúbicos?
Para resolver este problema, se establece un factor de conversión entre los litros y los metros cúbicos, posteriormente otra conversión para los metros y pies cúbicos.
Para pasar de litros a pies cúbicos, se multiplica la capacidad expresada en litros por el factor de conversión un metro cúbico sobre mil litros, y por el factor de conversión 35.315 pies cúbicos sobre un metro cúbico.
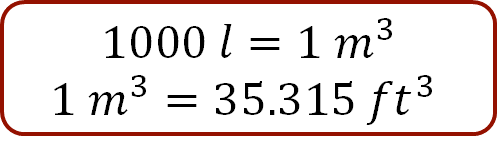
Ten presente que la conversión de unidades puede realizarse multiplicando sucesivamente la cantidad a convertir, en este caso, los mil cien litros por los factores de conversión necesarios para lograr las unidades deseadas, los pies cúbicos.
De esta manera la expresión a resolver es:
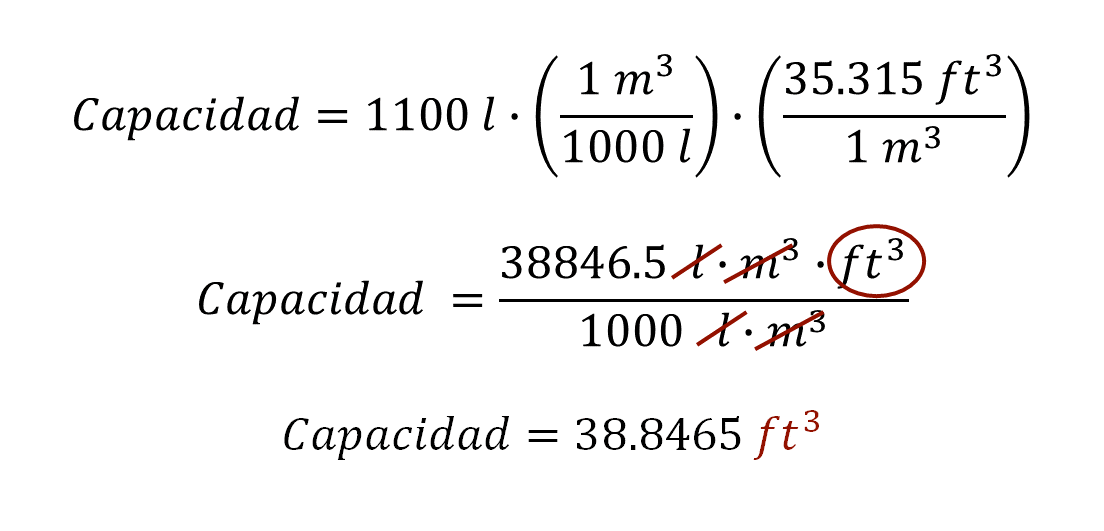
Entonces, la capacidad del tinaco, expresada en pies cúbicos, es equivalente a 38.8465 pies cúbicos.
Continúa poniendo en práctica los factores de conversión, resolviendo el siguiente problema.
Problema 5: cámara fría, metros cúbicos-pies cúbicos
Mary es dueña de una empresa de refrigeración. Por expansión debe instalar una cámara fría de 71 metros cúbicos. Al cotizarla le indican que el precio de instalación es de $110 por pie cúbico, ¿cuál será el costo aproximado de dicha instalación?
Para dar solución al problema, analiza los datos para poder plantear el factor o factores de conversión. En este caso, observa que hay que convertir la capacidad mostrada de metros cúbicos a pies cúbicos.
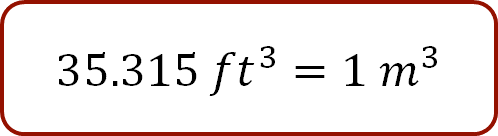
Posteriormente, se calcula el costo aproximado teniendo presente la referencia dada en la cotización, cada pie cúbico cuesta ciento diez pesos. ¿Cuánto estimas que será el costo de instalación de esa cámara fría?

Teniendo en cuenta la equivalencia entre pies y metros cúbicos, se establece la ecuación con el respectivo factor de conversión. De tal manera, queda planteada la siguiente relación.
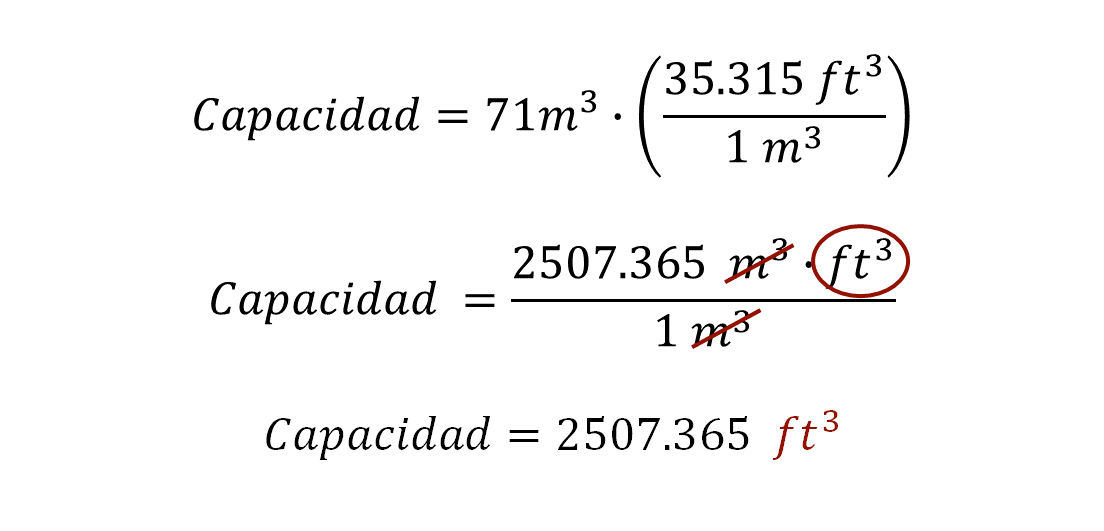
Por lo tanto, se obtienen 2507.365, el resultado se expresará en pies cúbicos. Se puede afirmar que la capacidad de la cámara de refrigeración que va a instalar Mary es de 2507.365 pies cúbicos.
Con esta información, ya se puede calcular el costo aproximado de la instalación.
El costo de instalación por pie cúbico es de ciento diez pesos; por lo tanto, para saber el costo de la instalación de la cámara de refrigeración bastará con multiplicar el costo proporcionado en la cotización, por la capacidad calculada anteriormente, es decir:
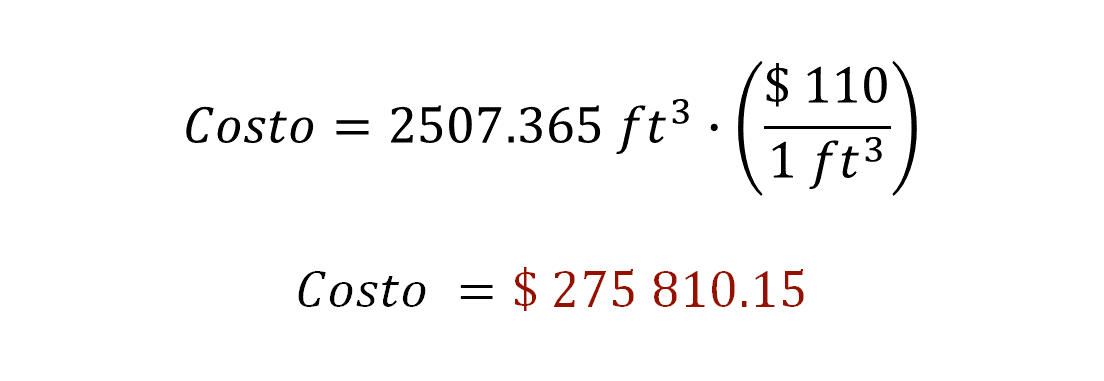
El resultado es 275,810.15 pesos, como costo de instalación de la cámara fría. Es posible aproximar este costo a 276,000 pesos, que es lo que Mary debe invertir para lograr instalar la cámara fría.
Como puedes notar, la clave para realizar conversiones de unidades está en conocer las equivalencias entre ellas, pues de esta manera es posible establecer los factores de conversión, y también se puede multiplicar por los factores de conversión necesarios con el fin de obtener las unidades de capacidad deseadas.
A continuación, se muestra una tabla con las medidas de capacidad y sus equivalencias utilizadas hasta el momento.

Un metro cúbico equivale a mil litros, un litro equivale a mil mililitros, un galón corresponde a 3.785 litros, una taza es equivalente a 240 mililitros, una onza de fluido es igual a 29.5735 mililitros y un metro cúbico es equivalente a 35.315 pies cúbicos.
De manera individual, o con ayuda de tu profesora o profesor de grupo, puedes plantear los factores de conversión que desees, por ejemplo, de metros cúbicos a galones, de onzas de fluido a metros cúbicos o los que te imagines en cuanto a unidades de capacidad se refiere, sólo debes tomar en cuenta la equivalencia entre unidades.
Utilizando las equivalencias anteriores, realicen los siguientes ejercicios.
Ejercicio 1: convierte 20 litros a tazas, para lograrlo, considera las equivalencias necesarias, en este caso, un litro es igual a mil mililitros y una taza es igual a 240 mililitros.

Antes de iniciar la resolución contesta en tu cuaderno las siguientes preguntas: ¿cuántos factores de conversión se deben aplicar para lograr esta conversión?, ¿cuál o cuáles son esos factores de conversión?
Son dos los factores de conversión que se deben aplicar en este problema.
Multiplica 20 litros por el factor mil mililitros sobre un litro y también por el factor una taza sobre 240 mililitros.
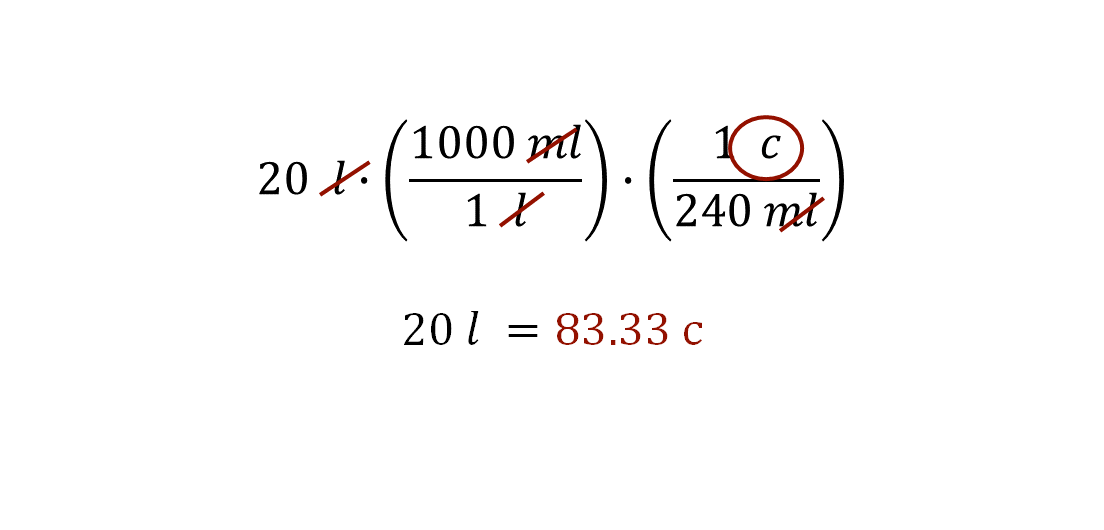
El resultado numérico de las operaciones es 83.33 tazas.
Ejercicio 2: convierte 6 galones a mililitros. Considera las equivalencias, un galón es igual 3.785 litros y un litro es igual a mil mililitros.
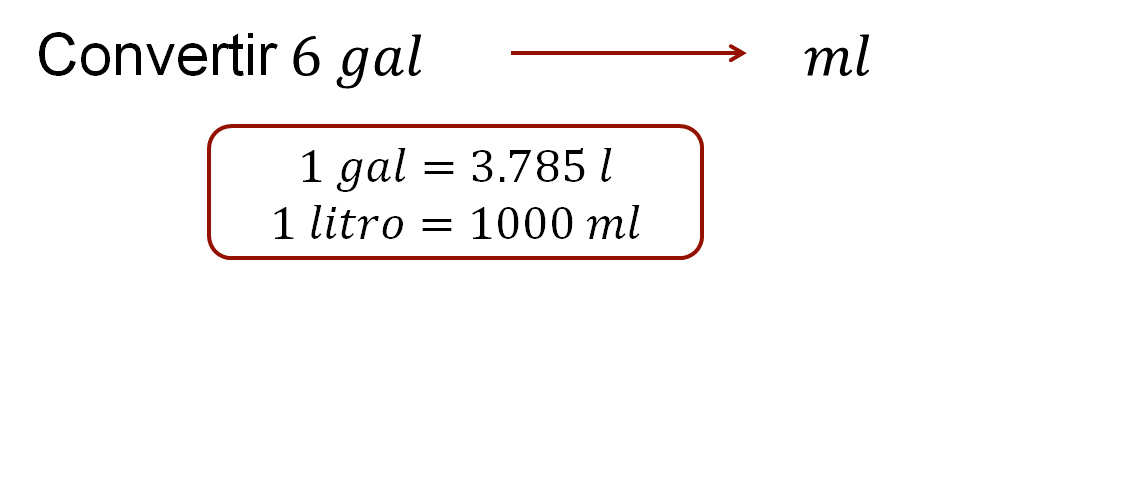
Con base en lo realizado hasta el momento, contesta: ¿cuántos factores de conversión se deben aplicar para determinar cuántos mililitros son equivalentes a seis galones? Realiza una estimación del número de mililitros que son equivalentes a seis galones y anótalo en tu cuaderno.
Al establecer la relación para esta conversión se utilizan los dos factores de conversión mencionados antes. Quedando de la siguiente manera:
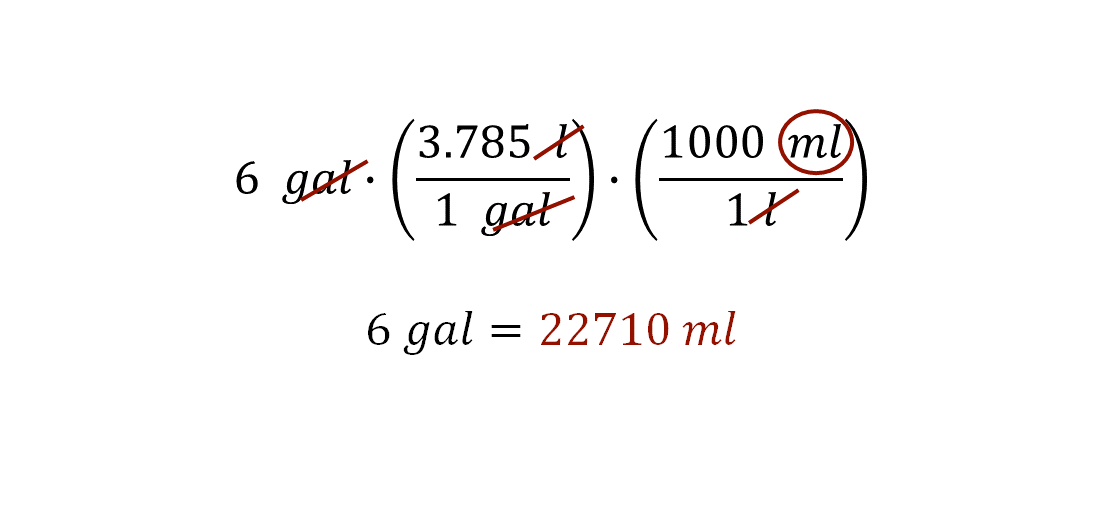
El resultado indica que seis galones equivalen a 22,710 mililitros. Compara este resultado con la estimación que hiciste antes de resolver este ejercicio.
Ejercicio 3: convierte treinta y cuatro onzas de fluido a litros. Considera las equivalencias, una onza de fluido equivale a 29.5735 mililitros y un litro es igual a mil mililitros.

Estima el resultado y contesta en tu cuaderno: ¿resultarán más de treinta cuatro litros o menos de treinta y cuatro litros?, ¿por qué?
Establece la relación para convertir, 34 onzas de fluido por el factor 29.5735 mililitros sobre una onza de fluido y también por el factor un litro sobre mil mililitros.
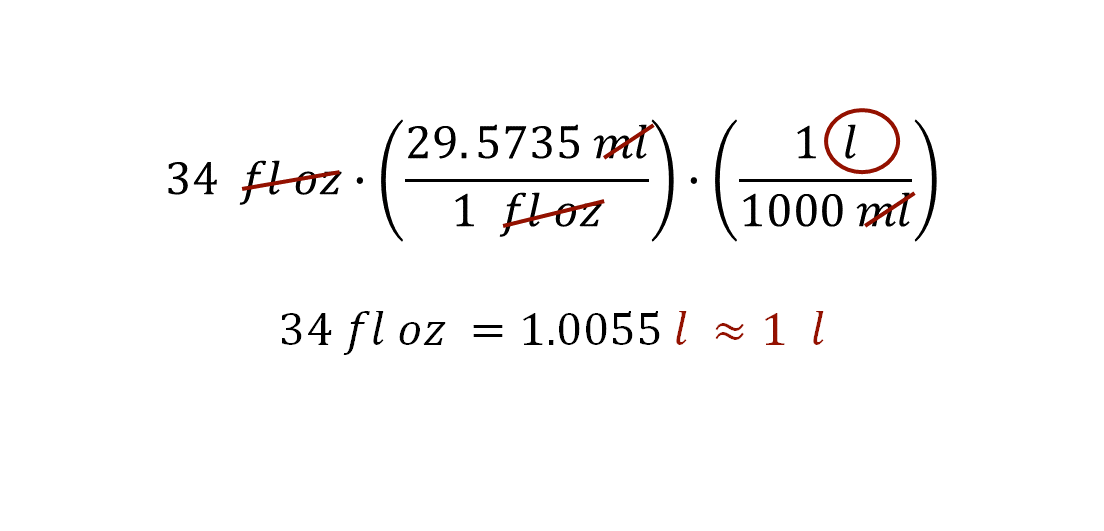
Al realizar las operaciones numéricas como la reducción de unidades, el resultado es 1.0055 litros. Es posible aproximar el resultado a un litro, es decir, 34 onzas de fluido equivalen aproximadamente a un litro.
Ejercicio 4: convierte noventa y seis mil tazas a metros cúbicos. Considera las siguientes equivalencias, una taza equivale a 240 mililitros, mil mililitros son iguales a un litro y, por último, mil litros equivalen a un metro cúbico.

De acuerdo con estas equivalencias, ¿cuántos factores de conversión se deben aplicar para determinar la equivalencia en este ejercicio?, ¿cuántos metros cúbicos estimas que son equivalentes a noventa y seis mil tazas?
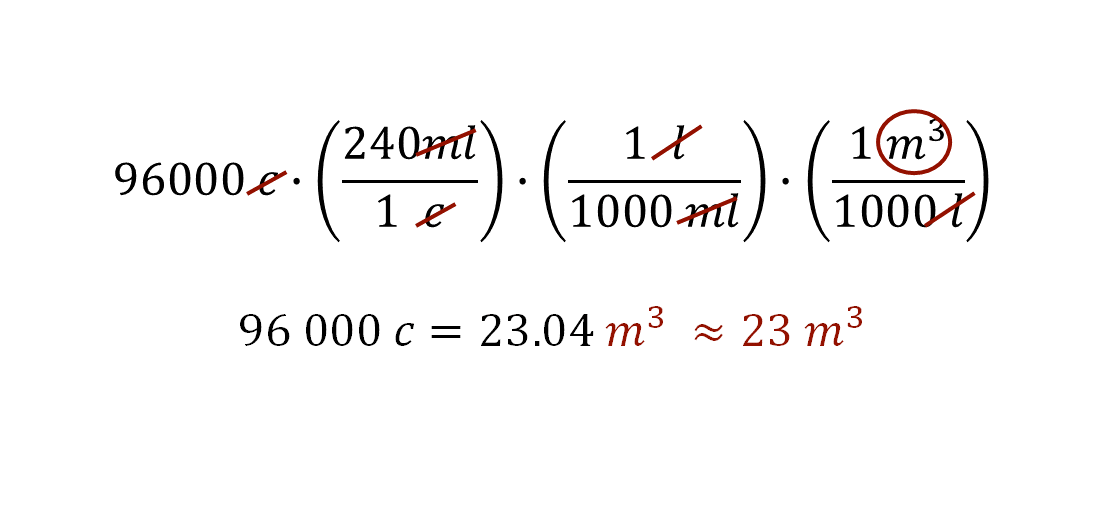
El resultado de la conversión de noventa y seis mil tazas es equivalente a 23.04 metros cúbicos, que se puede aproximar a 23 metros cúbicos.
En el caso de las conversiones, es primordial tener presentes las equivalencias entre unidades, para establecer los factores de conversión y lograr resolver correctamente los problemas que se presenten.
Con esto, has concluido la sesión. Recuera que éste es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí.
No hay comentarios.:
Publicar un comentario